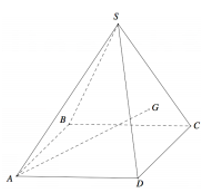
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi G là trọng tâm tam giác SCD (tham khảo hình vẽ bên). Tang góc giữa đường thẳng AG và mặt phẳng (ABCD) bằng
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Gọi O là tâm hình vuông ABCD và M là trung điểm CD có và H là hình chiếu vuông góc của G lên mặt phẳng (ABCD).
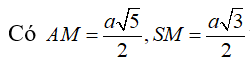
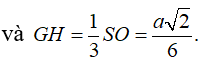
Vì
![]()
![]()
![]()
Và
![]()
![]()
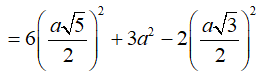
![]()
Vì vậy
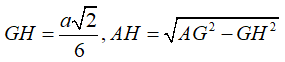
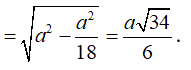
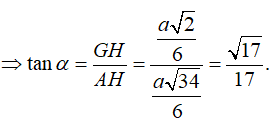
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA = a và vuông góc với mặt đáy. Gọi M là trung điểm cạnh SB (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng AM và SC bằng

Cho khối chóp S.ABCD có đáy là hình bình hành, AB=3, AD=4, Cạnh bên SA= vuông góc với đáy. Gọi M,N,P lần lượt là trung điểm các cạnh SA, AD và BC (tham khảo hình vẽ bên). Tính góc giữa hai mặt phẳng (SBC) và (MNP).

Cho tứ diện đều ABCD. Gọi M là trung điểm cạnh AC (tham khảo hình vẽ bên). Tang góc giữa đường thẳng BM và mặt phẳng (BCD) bằng
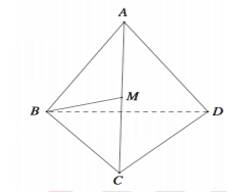
Cho khối tứ diện đều ABCD cạnh a. Gọi E là điểm đối xứng của A qua D. Mặt phẳng qua CE và vuông góc với mặt phẳng (ABD) cắt cạnh AB tại điểm F. Tính thể tích V của khối tứ diện AECF.
Cho hình hộp ABCD.A'B'C'D' có tất cả các mặt là hình thoi và các góc đỉnh A bằng (tham khảo hình vẽ bên). Góc giữa hai đường thẳng BD và A′C bằng
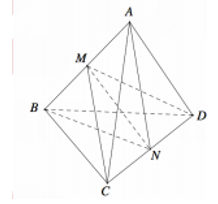
Cho hình tứ diện ABCD. Gọi M , N lần lượt là trung điểm các cạnh AB và CD. Biết AB=CD=AN=BN=CM=MD =a (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng AB và CD bằng
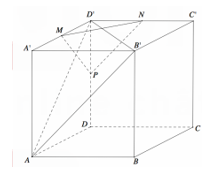
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=4 AD =5 AA'=6 . Gọi M , N , P lần luợt là trung điểm các cạnh A'D', C'D' và DD' (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (AB'D') và bằng (MNP)
Cho hình chóp tứ giác đều S.ABCD có tất cả cạnh bằng a (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng SA và CD bằng

Cho hình nón có bán kính đáy bằng a, độ dài đường sinh bằng 2a. Góc ở đỉnh của hình nón bằng
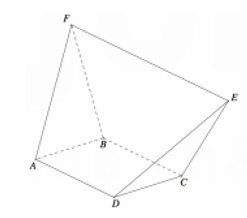
Cho hình vuông ABCD. Dựng khối da diện ABCDEF , trong đó EF =2a và song song với AD (tham khảo hình vẽ bên). Tất cả các cạnh còn lại của khối đa diện ABCDEF bằng a. Tính thể tích V của khối đa diện ABCDEF.
Cho hai điểm A,B cố định,AB=1. Tập hợp các điểm M trong không gian sao cho diện tích tam giác MAB bằng 4 là một mặt trụ. Tính bán kính r của mặt trụ đó.
Cho hình trụ (T) có MN , PQ vuông góc với nhau lần lượt là hai đường kinh nằm trên hai đường tròn đáy của hình trụ. Thể tích khối tứ diện MNPQ bằng 10. Tính thể tích của khối trụ (T).
Cho hai tam giác đều ABC và ABD có độ dài cạnh bằng 1 và nằm trong hai mặt phẳng vuông góc. Gọi S là điểm đối xứng của B qua đường thẳng DC. Tính thể tích của khối đa diện ABDSC.
Thể tích của khối hộp chữ nhật có độ dài các cạnh bằng a, b, c là