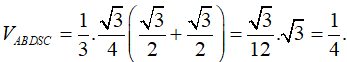20 câu hỏi trắc nghiệm thuộc Bài tập Hình học không gian ôn thi THPT Quốc gia có lời giải (P2)

Câu 1:

Cho hình chóp tứ giác đều S.ABCD có tất cả cạnh bằng a (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng SA và CD bằng

A. $\frac{a \sqrt{6}}{6}$

B. $\frac{a \sqrt{3}}{3}$

C. $\frac{a \sqrt{3}}{6}$

D. $\frac{a \sqrt{6}}{3}$

Xem đáp án

Đáp án D

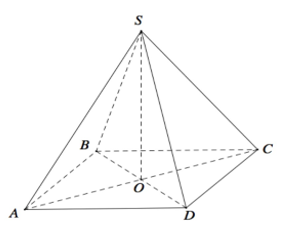
Mặt khác S.OAB là tứ diện vuông đỉnh O nên

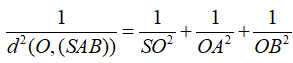
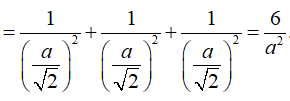
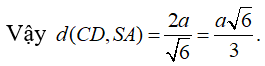
Câu 2:

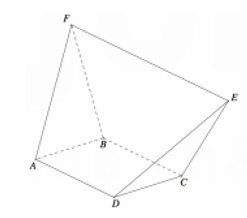
Cho khối tứ diện đều ABCD cạnh a. Gọi E là điểm đối xứng của A qua D. Mặt phẳng qua CE và vuông góc với mặt phẳng (ABD) cắt cạnh AB tại điểm F. Tính thể tích V của khối tứ diện AECF.

A. $\frac{\sqrt{2} a^{3}}{30}$

B. $\frac{\sqrt{2} a^{3}}{60}$

C. $\frac{\sqrt{2} a^{3}}{40}$

D. $\frac{\sqrt{2} a^{3}}{15}$

Xem đáp án

Đáp án D

Gọi G là trọng tâm tam giác ABD

=> (CEF) là mặt phẳng cần dựng.

Ta tính được

Câu 3:

Cho khối chóp S.ABCD có đáy là hình bình hành, AB=3, AD=4, $\hat{B A D} = 120^{o}$ Cạnh bên SA= $2 \sqrt{3}$ vuông góc với đáy. Gọi M,N,P lần lượt là trung điểm các cạnh SA, AD và BC (tham khảo hình vẽ bên). Tính góc giữa hai mặt phẳng (SBC) và (MNP).

A. $60^{o}$

B. $45^{o}$

C. $90^{o}$

D. $30^{o}$

Xem đáp án

Đáp án B

Ta có

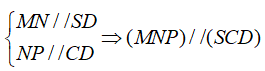
Tính được

Ta có

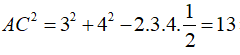
Tam giác SBC có

Tam giác

Vì vậy

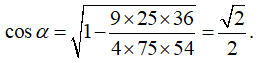
Câu 4:

Cho hai điểm A,B cố định,AB=1. Tập hợp các điểm M trong không gian sao cho diện tích tam giác MAB bằng 4 là một mặt trụ. Tính bán kính r của mặt trụ đó.

A. r = 4

B. r = 2

C. r = 1

D. r = 8

Xem đáp án

Đáp án D

Ta có

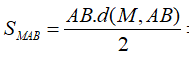
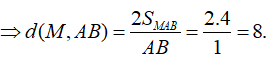
Vậy M thuộc mặt trụ có trục AB và bán kính r = 8

Câu 5:

Thể tích của khối lập phương có độ dài cạnh bằng 6 là

A. 72.

B. 216.

C. 108.

D. 36.

Xem đáp án

Đáp án B

Câu 6:

Cho hình nón có thiết diện qua trục là một tam giác đều cạnh bằng 1. Tìm chiều cao của hình nón.

A. $h = \frac{\sqrt{2}}{2}$ .

B. $h = \frac{3}{4}$ .

C. $h = \frac{1}{2}$ .

D. $h = \frac{\sqrt{3}}{2}$

Xem đáp án

Đáp án D

Thiết diện qua trục là một tam giác cân có độ dài cạnh 2r, l, l vậy theo giả thiết có

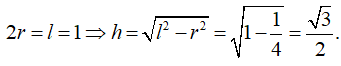
Câu 7:

Cho hình hộp ABCD.A'B'C'D' có tất cả các mặt là hình thoi và các góc đỉnh A bằng $60^{o}$ (tham khảo hình vẽ bên). Góc giữa hai đường thẳng BD và A′C bằng

A. $90^{o}$

B. $30^{o}$

C. $45^{o}$

D. $60^{o}$

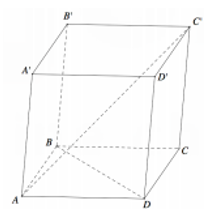
Xem đáp án

Đáp án A

=>(ACC') là mặt phẳng trung trực của BD.

Do đó

Câu 8:

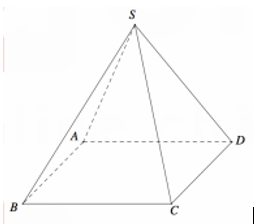
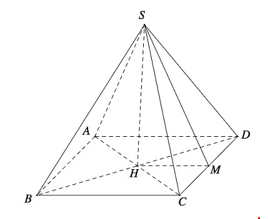
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (SCD) và (ABCD) bằng

A. $\frac{\sqrt{3}}{3}$

B. $\frac{1}{2}$

C. $\frac{\sqrt{3}}{2}$

D. $\frac{\sqrt{3}}{6}$

Xem đáp án

Đáp án A

Gọi H là tâm mặt đáy và M là trung điểm cạnh

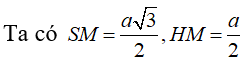
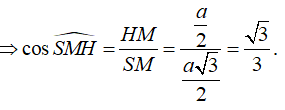
Câu 9:

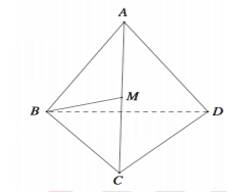
Cho tứ diện đều ABCD. Gọi M là trung điểm cạnh AC (tham khảo hình vẽ bên). Tang góc giữa đường thẳng BM và mặt phẳng (BCD) bằng

A. $\frac{\sqrt{3}}{6}$

B. $\frac{\sqrt{2}}{3}$

C. $\frac{\sqrt{14}}{7}$

D. $\frac{\sqrt{14}}{2}$

Xem đáp án

Đáp án C

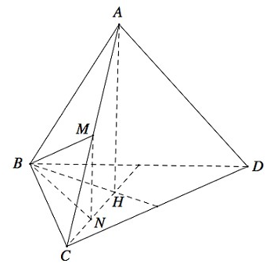
Gọi H là tâm mặt đáy, ta có AH $⊥$ (BCD) và gọi N là trung điểm

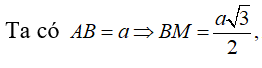
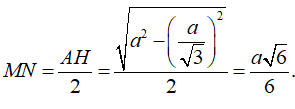
Do đó

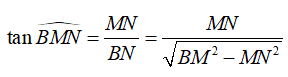
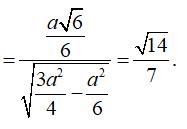
Câu 10:

Cho hình trụ (T) có MN , PQ vuông góc với nhau lần lượt là hai đường kinh nằm trên hai đường tròn đáy của hình trụ. Thể tích khối tứ diện MNPQ bằng 10. Tính thể tích của khối trụ (T).

A. 60 $π$

B. 30 $π$

C. 45 $π$

D. 15 $π$

Xem đáp án

Đáp án D

Ta có MN= PQ = 2r

Do đó

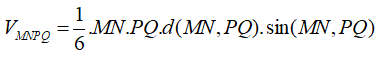
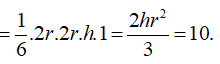
Vì vậy

Câu 11:

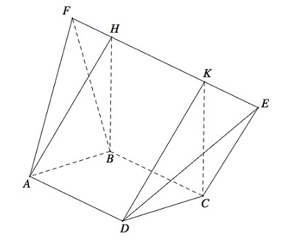
Cho hình vuông ABCD. Dựng khối da diện ABCDEF , trong đó EF =2a và song song với AD (tham khảo hình vẽ bên). Tất cả các cạnh còn lại của khối đa diện ABCDEF bằng a. Tính thể tích V của khối đa diện ABCDEF.

A. $V = \frac{\sqrt{2} a^{3}}{6}$

B. $V = \frac{5 \sqrt{2} a^{3}}{6}$

C. $V = \frac{\sqrt{2} a^{3}}{3}$

D. $V = \frac{\sqrt{2} a^{3}}{12}$

Xem đáp án

Đáp án C

Gọi H, K lần lượt là hình chiếu vuông góc của A, D lên EF ta có

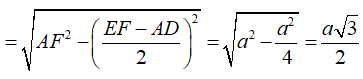
Vì vậy

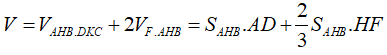
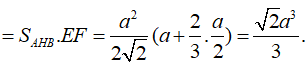
Câu 12:

Cho hình lăng trụ tam giác đều ABC.A′B′C’ có AB = 2, AA' = $2 \sqrt{3}$ (tham khảo hình vẽ bên). Tính khoảng cách giữa hai đường thẳng AB’ và A’C

A. $\frac{2 \sqrt{17}}{17}$

B. $\frac{2 \sqrt{39}}{13}$

C. $\frac{2 \sqrt{33}}{11}$

D. $\frac{\sqrt{3}}{2}$

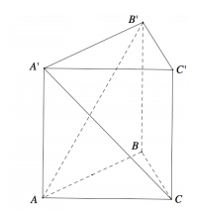
Xem đáp án

Đáp án B

Gọi I, M lần lượt là trung điểm AB′, BC

Do đó

Câu 13:

Thể tích của khối hộp chữ nhật có độ dài các cạnh bằng a, b, c là

A. $\frac{1}{6}$ abc

B. $\frac{1}{2}$ abc

C. abc

D. $\frac{1}{3}$ abc

Xem đáp án

Đáp án C

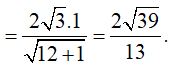
Câu 14:

Cho hình nón có bán kính đáy bằng a, độ dài đường sinh bằng 2a. Góc ở đỉnh của hình nón bằng

A. $30^{o}$

B. $120^{o}$

C. $60^{o}$

D. $150^{o}$

Xem đáp án

Đáp án C

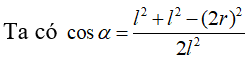
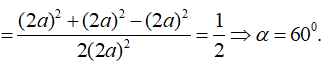
Câu 15:

Cho hình tứ diện ABCD. Gọi M , N lần lượt là trung điểm các cạnh AB và CD. Biết AB=CD=AN=BN=CM=MD =a (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng AB và CD bằng

A. $\frac{a \sqrt{3}}{3}$

B. $\frac{a \sqrt{3}}{2}$

C. $\frac{a \sqrt{3}}{6}$

D. $\frac{a \sqrt{2}}{2}$

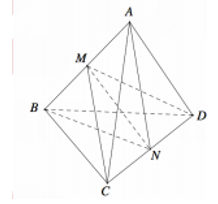
Xem đáp án

Đáp án B

Giả thiết có

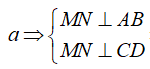
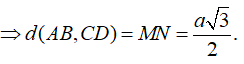
Câu 16:

Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA = a $\sqrt{3}$ và vuông góc với mặt đáy. Gọi M là trung điểm cạnh SB (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng AM và SC bằng

A. $\frac{5}{16}$

B. $\frac{11}{16}$

C. $\frac{5}{8}$

D. $\frac{3}{8}$

Xem đáp án

Đáp án C

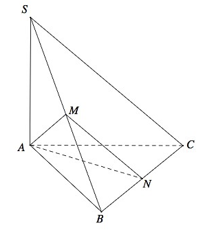
Gọi N là trung điểm BC, có

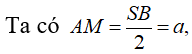
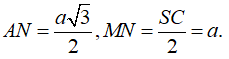
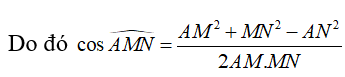
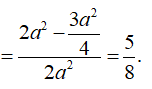
Câu 17:

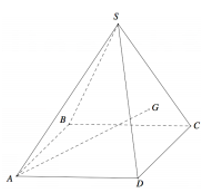
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi G là trọng tâm tam giác SCD (tham khảo hình vẽ bên). Tang góc giữa đường thẳng AG và mặt phẳng (ABCD) bằng

A. $\frac{\sqrt{17}}{17}$

B. $\frac{2 \sqrt{5}}{5}$

C. $\frac{\sqrt{5}}{5}$

D. $\frac{2 \sqrt{17}}{17}$

Xem đáp án

Đáp án A

Gọi O là tâm hình vuông ABCD và M là trung điểm CD có $S O = \frac{a \sqrt{2}}{2}$ và H là hình chiếu vuông góc của G lên mặt phẳng (ABCD).

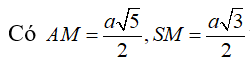
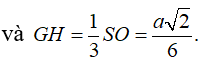
Vì

Và

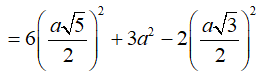
Vì vậy

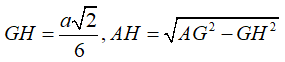
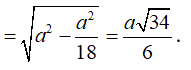
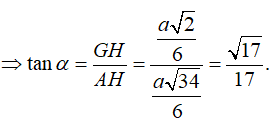
Câu 18:

Cho hình trụ (T) có diện tích đáy bằng 48π và hai dây cung AB,CD lần lượt nằm trên hai đường tròn đáy của (T) sao cho ABCD là một hình vuông có độ dài cạnh bằng 10 và các cạnh của hình vuông này không song song với đường sinh của (T) (tham khảo hình vẽ bên). Tính thể tích của khối trụ (T).

A. 288π

B. $96 \sqrt{2}$ π

C. $192 \sqrt{2}$ π.

D. 384π

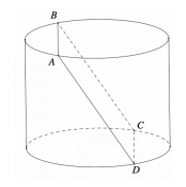
Xem đáp án

Đáp án B

Giả sử hình vuông ABCD có độ dài cạnh a.

Kẻ các đường sinh AH,BK ta có

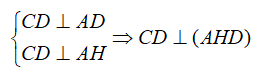
Theo pitago ta có

Câu 19:

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=4 AD =5 AA'=6 . Gọi M , N , P lần luợt là trung điểm các cạnh A'D', C'D' và DD' (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (AB'D') và bằng (MNP)

A. $\frac{181}{469}$

B. $\frac{120 \sqrt{13}}{469}$

C. $\frac{19}{469}$

D. $\frac{60 \sqrt{61}}{469}$

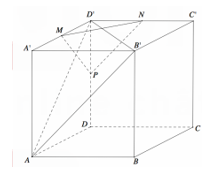
Xem đáp án

Đáp án A

Chọn hệ trục toạ độ sao cho

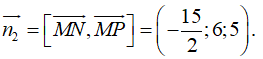
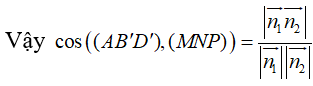
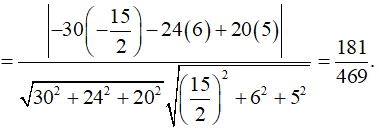
Câu 20:

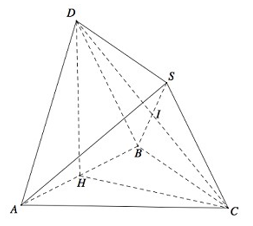
Cho hai tam giác đều ABC và ABD có độ dài cạnh bằng 1 và nằm trong hai mặt phẳng vuông góc. Gọi S là điểm đối xứng của B qua đường thẳng DC. Tính thể tích của khối đa diện ABDSC.

A. $\frac{3}{4}$

B. $\frac{3}{8}$

C. $\frac{1}{2}$

D. $\frac{1}{4}$

Xem đáp án

Đáp án D

Gọi I,H lần lượt là trung điểm của CD,AB.

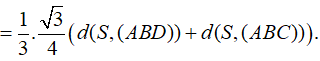
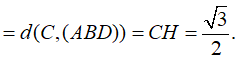
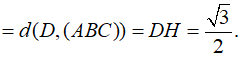
Vậy