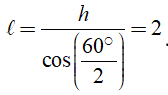Bài tập Hình học không gian ôn thi THPT Quốc gia có lời giải (P9)
-
5415 lượt thi
-
21 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
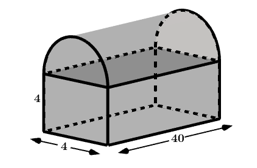
Một thùng thư, được thiết kế như hình vẽ bên, phần phía trên là nữa hình trụ. Thể tích của thùng đựng thư là
 Xem đáp án
Xem đáp án
Chọn B
Thể tích phần phía dưới là
![]()
Thể tích phần bên trên là
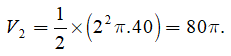
![]()
Câu 2:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB, C'D' bằng
 Xem đáp án
Xem đáp án
Chọn B.
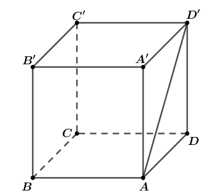
![]()
Câu 3:
Vật thể nào trong các vật thể sau không phải là khối đa diện?
 Xem đáp án
Xem đáp án
Chọn C.
Vì hình C vi phạm tính chất Mỗi cạnh của miền đa giác nào cũng là cạnh chung của đúng hai miền đa giác .
Câu 4:
Một vật thể nằm giữa hai mặt phẳng x = -1 và x = 1 thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ x (-1x 1) là một hình tròn có diện tích bằng 3 Thể tích của vật thể bằng
 Xem đáp án
Xem đáp án
Chọn B
Thể tích của vật thể
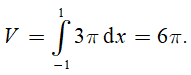
Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M và N lần lượt là trung điểm của BC và CD (tham khảo hình vẽ bên). Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.CMN
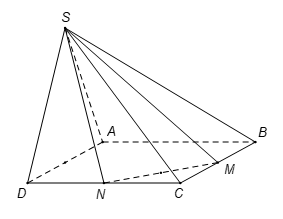
 Xem đáp án
Xem đáp án
Chọn D.
Áp dụng công thức tìm nhanh bán kính mặt cầu ngoại tiếp hình chóp với
r là bán kính đường tròn ngoại tiếp đa giác đáy
: S là đỉnh hình chóp , O là tâm đường tròn ngoại tiếp đa giác đáy, h là chiều cao hình chóp
Cụ thể vào bài toán:
Đáy là tam giác CMN vuông tại C
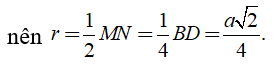
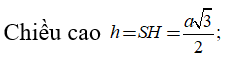
Tâm O của đường tròn ngoại tiếp tam giác CMN là trung điểm MN
Áp dụng công thức đường trung tuyến trong tam giác HMN tính được
Trong tam giác vuông SHO có
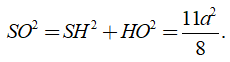
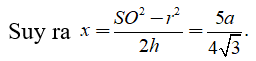
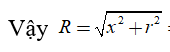
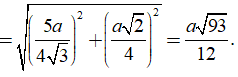
Câu 6:
Cho tứ diện ABCD trên các cạnh BC, BD, AC lần lượt lấy các điểm M, N, P sao cho BC = 3BM, BD = BN, AC = 2AP. Mặt phẳng (MNP) chia khối tứ diện thành hai phần có thể tích là và . Tỷ số có giá trị bằng
 Xem đáp án
Xem đáp án
Chọn B.
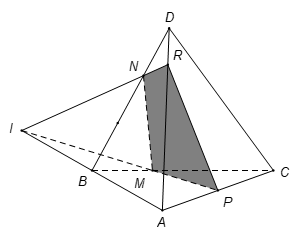
Lời khuyên cho giáo viên nên cho học sinh biết định lý Menelauyt để làm trắc nghiệm về phần này cho nhanh, việc chứng minh định lý cũng hoàn toàn đơn giản (dựa vào Talet).
Chắc chắn ta cần tính tỉ số và
Theo Menelauyt, ta có
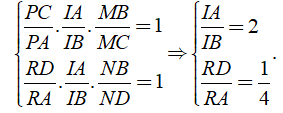
Suy ra M là trọng tâm của tam giác CAI
![]()
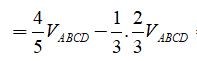
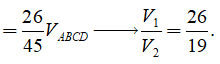
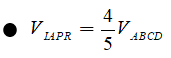
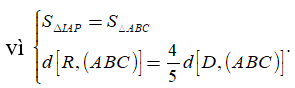
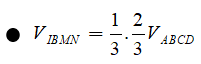
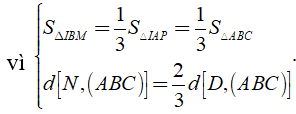
Câu 7:
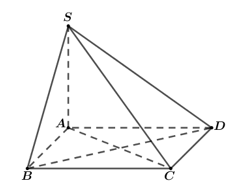
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA = x và vuông góc với đáy (ABCD). Xác định x để hai mặt phẳng (SBC) và (SCD) hợp với nhau góc
 Xem đáp án
Xem đáp án
Chọn B
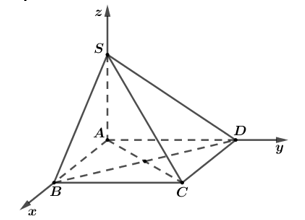
Để cho gọn ta chọn a =1
Chọn hệ trục tọa độ sao cho A = O(0;0;0) và B(1;0;0), D(0;1;0) S(0;0;x) với x = SA >0
Suy ra C(1;1;0)
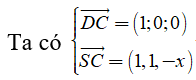
=> VTPT của mặt phẳng (SCD) là
![]()
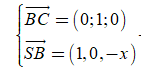
=> VTPT của mặt phẳng (SBC) là
![]()
Từ giả thiết bài toán, ta có
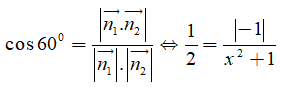
![]()
Câu 8:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB =a. Cạnh bên SA vuông góc với mặt phẳng đáy, góc tạo bởi hai mặt phẳng (ABC) và (SBC) bằng (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng AB và SC bằng

 Xem đáp án
Xem đáp án
Chọn C
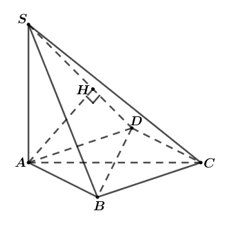
Xác định được
![]()
Khi đó ta tính được
![]()
Trong mặt phẳng (ABC) lấy điểm D sao cho ABCD là hình chữ nhật => AB//(SCD) nên
![]()
![]()
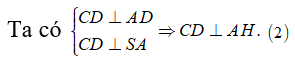
Từ (1) và (2) suy ra
![]()
Xét tam giác vuông SAD có
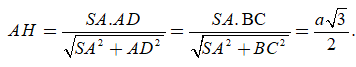
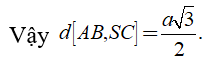
Câu 9:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm của CD góc giữa SM và mặt phẳng đáy bằng Độ dài cạnh SA bằng
 Xem đáp án
Xem đáp án
Chọn D.
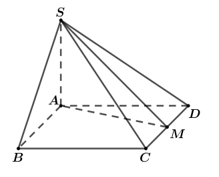
![]()
nên AM là hình chiếu của SM lên (ABCD).
Do đó góc giữa SM và (ABCD) là
Ta có
![]()
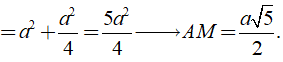
Xét tam giác SAM vuông tại A, có
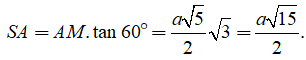
Câu 10:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Khoảng cách từ điểm A đến mặt phẳng bằng (A'BD)
 Xem đáp án
Xem đáp án
Chọn D.
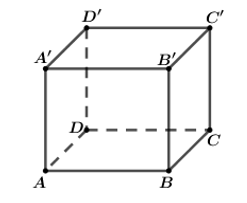
Xét hình chóp AA'BD có AA' = AB = AD và đôi một vuông góc với nhau nên
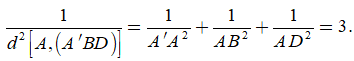
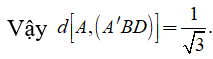
Câu 11:
Một khối nón và một khối trụ có chiều cao và bán kính đáy đều bằng 1. Tổng thể tích của khối nón và khối trụ đó là
 Xem đáp án
Xem đáp án
Chọn B.
Thể tích khối nói
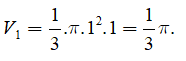
Thể tích khối trụ
![]()
Tổng thể tích
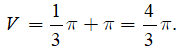
Câu 13:
Trong không gian với hệ tọa độ Oxyz cho hình lăng trụ tam giác đều ABC. có hai đỉnh B, C thuộc trục Oz và AA'=1 ( C không trùng O). Biết là một véc tơ chỉ phương của đường thẳng .Tính
 Xem đáp án
Xem đáp án
Chọn D
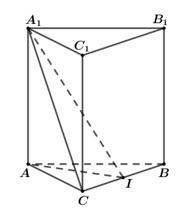
Gọi I là trung điểm của BC => I(0; 0; 1)
![]()
![]()
=> I là hình chiếu vuông góc của trên Oz
![]()
![]()
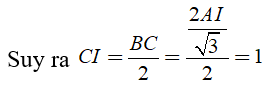
(do tam giác ABC đều)
![]()
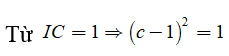
Trường hợp 1: c= 0 (loại)
Trường hợp 2: c =2
![]()
Chọn VTCP của C là
![]()
Câu 14:
Xét một hình trụ nội tiếp trong hình nón như hình bên, trong đó S là đỉnh hình nón, O là tâm đường tròn mặt đáy. Các đoạn AB, CD lần lượt là đường kính của đường tròn đáy của hình nón và hình trụ. Biết AC, BD cắt nhau tại điểm M (MSO) tỉ số thể tích của hình trụ và hình nón là . Tính tỉ số
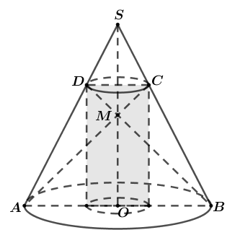
 Xem đáp án
Xem đáp án
Chọn C.
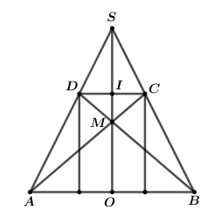
Gọi I là trung điểm DC
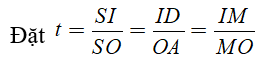
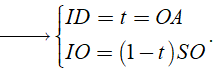
Theo giả thiết ta có
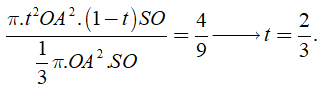
Suy ra
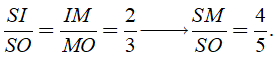
Câu 15:
Tứ diện OABC có OA, OB, OC đôi một vuông góc và OA =1, OB =2, OC =3. Tan của góc giữa đường thẳng OA và mặt phẳng (ABC) bằng
 Xem đáp án
Xem đáp án
Chọn C.
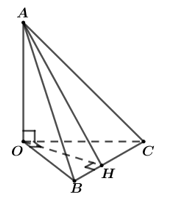
![]()
ta chứng minh được
![]()
Ta có
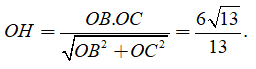
Vậy
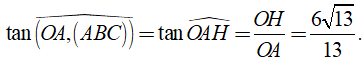
Câu 16:
Cho hình chóp S.ABCD có đáy là hình thoi cạnh bằng a, Cạnh bên SD vuông góc với đáy (ABCD) và (SAB)(SBC) (tham khảo hình vẽ). Khoảng cách giữa hai đường thẳng SA và BD bằng
 Xem đáp án
Xem đáp án
Chọn C
Để cho gọn ta chọn a=2
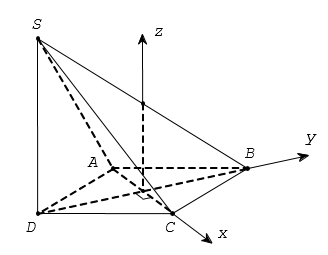
Chọn hệ trục tọa độ Oxyz như hình vẽ với O(0;0;0) và C(1;0;0), B(0;;0) S(0; -; x) với x =SD>0
Suy ra A(-1;0;0) và D(0;-;0)
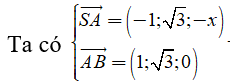
VTPT của mặt phẳng (SAB) là
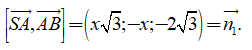
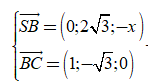
VTPT của mặt phẳng (SBC) là
![]()
Từ giả thiết bài toán, ta có
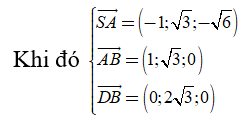
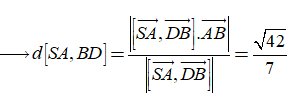
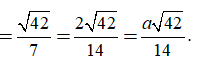
Câu 17:
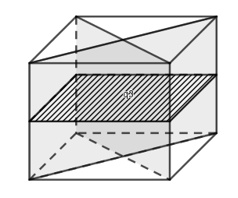
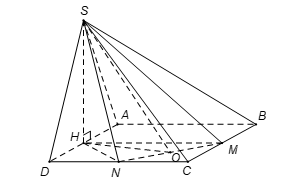
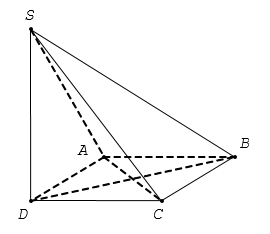
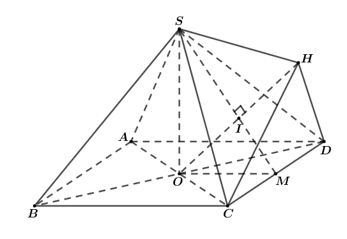
Cho khối chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh bằng a, tâm O cạnh bên bằng a. Gọi M là trung điểm của CD, H là điểm đối xứng của O qua SM (tham khảo hình vẽ bên). Thể tích khối đa diện ABCDSH bằng
 Xem đáp án
Xem đáp án
Chọn D
Khối đa diện ABCDSH được chia thành hai khối chóp S.ABCD và H.SCD
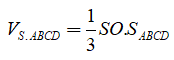
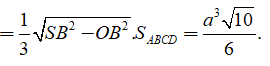
Vì H là điểm đối xứng của O qua SM nên
![]()
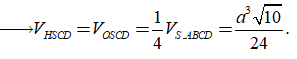
Vậy thể tích khối đa diện cần tính bằng
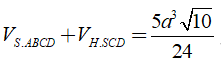
Câu 18:
Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a. Gọi M, N lần lượt là trung điểm các cạnh AB, B'C'. Côsin góc giữa hai đường thẳng MN và AC bằng
 Xem đáp án
Xem đáp án
Chọn D
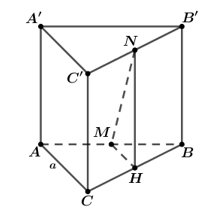
Gọi H là trung điểm của BC suy ra MH//AC
![]()
Ta có
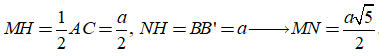
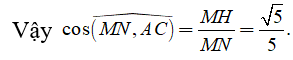
Câu 19:
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, AB=a, AC =a và BB'C'C là hình vuông. Khoảng cách giữa hai đường thẳng AA' và BC' là
 Xem đáp án
Xem đáp án
Chọn A.
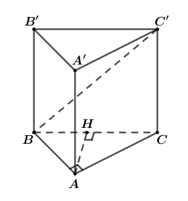
Gọi H là hình chiếu của A lên BC. Ta có
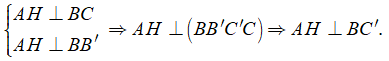
Suy ra AH là đoạn vuông góc chung của AA' và BC' nên
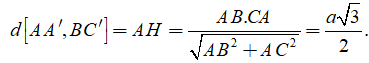
Câu 20:
Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm của tam giác BCD. Tính thể tích V của khối chóp A.GBC
 Xem đáp án
Xem đáp án
Chọn B.
Vì G là trọng tâm của tam giác BCD nên
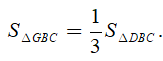
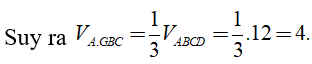
Câu 21:
Hình nón có góc ở đỉnh bằng và chiều cao bằng Độ dài đường sinh của hình nón bằng
 Xem đáp án
Xem đáp án
Chọn A
Đường sinh hình nón