Tính thể tích của một khối cầu biết hình lập phương cạnh a nội tiếp trong mặt cầu tạo nên khối cầu đó.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C.
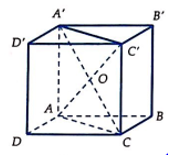
Gọi khối lập phương nội tiếp là ABCD.A'B'C'D'.
Gọi O = A'CAC' thì O cũng là tâm mặt cầu ngoại tiếp.
=> Bán kính của mặt cầu là
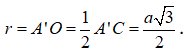
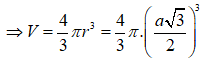
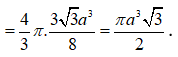
Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh 3a. Hình chiếu vuông góc của C’ lên mặt phẳng (ABC) là điểm D thỏa mãn . Góc giữa đường thẳng AC’ và mặt phẳng (A'B'C') bằng . Tính theo a thể tích khối lăng trụ ABC.A'B'C'.
Cho khối chóp tứ giác đều S.ABCD có cạnh bằng a, cạnh bên SC tạo với mặt đáy một góc .Tính thể tích của khối chóp S. ABCD
Cho tam giác đều ABC cạnh a. Gọi (P) là mặt phẳng chứa BC và vuông góc với mặt phẳng (ABC). Trong (P), xét đường tròn (C) đường kính BC. Diện tích mặt cầu nội tiếp hình nón có đáy là (C), đỉnh là A bằng
Một thùng hình trụ có thể tích bằng 12, chiều cao bằng 3. Diện tích xung quang của thùng đó là:
Cho lăng trụ ABC.A'B'C' có thể tích V. Tính thể tích của khối chóp A'.ABC theo V.
Cho khối nón có bán kính đáy r = và chiều cao gấp 2 lần bán kính đáy. Tính thể tích khối nón đã cho
Tính diện tích xung quanh của khối trụ có bán kính đáy r = 2 và độ dài đường sinh l =
Một cái hộp hình lăng trụ đứng đáy là hình vuông cạnh bằng 4cm. Chiều cao tối thiểu của hộp có thể đựng được 5 quả cầu bán kính 1cm là:
Cho lăng trụ ABC.A'B'C', trên cạnh AA'', BB' lấy các điểm M, N sao cho AA' = 3A'M; BB' = 3B'N. Mặt phẳng (C'MN) chia khối lăng trụ đã cho thành hai phần. Gọi là thể tích khối chóp C'.A'B'NM, là thể tích khối đa diện ABC.MNC'. Tính tỉ số
Cho hình nón có chiều cao bằng 2. Gọi là mặt phẳng đi qua đỉnh S của hình nón và cắt mặt đáy hình nón theo một dây cung AB và tạo với đáy hình nón một góc . Tính diện tích của mặt cắt SAB. Biết dây cung AB có số đo .
Cho hình chóp S.ABC có thể tích V. Gọi M, N, P là các điểm thỏa mãn SA = 2SM; SB = 2SN; SC = SP. Tính thể tích của khối chóp S.MNP theo V.
Cho hình chóp S. ABC, đáy tam giác ABC có diện tích bằng . Cạnh bên SA = 2 cm và SA (ABC). Tính thể tích của khối chóp S.ABC.
Cho khối chóp S.ABC có SA vuông góc với (ABC), tam giác ABC vuông tại A, AB=4a, AC=SA=3a. Tính thể tích của khối chóp S.ABC.
Thể tích của khối lăng trụ tam giác đều, có tất cả các cạnh bằng a là :
Cho khối lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB = a, AC = a. Mặt bên BCC’B’ là hình vuông. Tính thể tích của khối lăng trụ đã cho