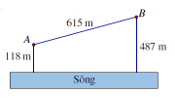
Cho hai vị trí A, B cách nhau 615m, cùng nằm về một phía bờ song như hình vẽ. Khoảng cách từ A và từ B đến bờ sông lần lượt là 118m và 478m . Một người đi từ A đến bờ sông để lấy nước mang về B . Đoạn đường ngắn nhất mà người đó có thể đi là
A. 569,5m.
B. 671, 4 m.
C. 779,8m.
D. 741, 2 m.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C

Cách 1: Giải bằng hàm số
Đặt CM = x (x > 0)
Dễ tính ra CD ![]()
Từ đề bài ta có: f (x) = ![]()
Quãng đường ngắn nhất người đó có thể đi
Giá trị nhỏ nhất của f(x) trên (0;492)
Ta có: f’(x) = 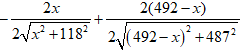
=> f’(x) = 0
![]()
![]()
![]()
![]()
![]()
Ta có bảng biến thiên
|
x |
0 |
0 |
492 |
|
y’ |
|
+ 0 - |
|
|
y |
779,8 |
||
Vậy quãng đường ngắn nhất mà người đó có thể đi là: 779,8
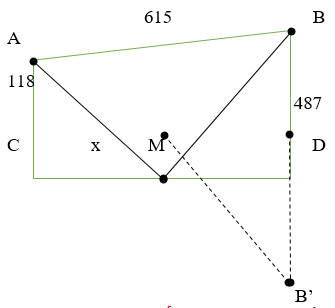
Cách 2: Giải bằng hình học
Gọi B’ là điểm đối xứng của B qua D
Dễ thấy AM + MB = AM + MB’
AM + MB ngắn nhất
AM + MB’ ngắn nhất
Dễ thấy theo bất đẳng thức tam giác: AM + MB’ ≥ AB’
AM + MB’ ngắn nhất ó AM + MB’ = AB’
Dấu “=” xảy ra khi và chỉ khi A, M, B’ thẳng hàng
Cho tứ diện đều ABCD cạnh bằng a. Khoảng cách d giữa hai đường thẳng AD và BC là:
Một hình trụ có diện tích xung quanh là thiết diện qua trục là hình vuông. Một mặt phẳng () song song vưới trục, cắt hình trụ theo thiết diện ABB’A’, biết một cạnh của thiết diện là một dây của đường tròn đáy hình trụ và căng một cung . Diện tích thiết diện ABB’A’ là
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 2AD = 3AA' = 6a. Thể tích của khối hộp chữ nhật ABCD.A'B'C'D' là:
Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = 3a, BC = 4a, SA = 12a và SA vuông góc với đáy. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD
Cho hình chóp S.ABC có (SAB), (SAC) cùng vuông góc vưới mặt phẳng đáy, cạnh bên SB tạo với đáy một góc . Đáy ABC là tam giác vuông cân tại B với Gọi M, N lần lượt là trung điểm của SB, SC. Tính thể tích của khối đa diện ABMNC
Cho hình tứ diện ABCD có DA = BC = 5, AB = 3, AC = 4. Biết DA vuông góc với mặt phẳng (ABC). Thể tích của khối tứ diện ABCD là:
Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng . Tính khoảng cách giữa hai đường thẳng AB' và A'C'
Cho hình chóp S.ABC, trên các cạnh SA, SB, SC lần lượt lấy các điểm A', B', C' sao cho SA' = SA, SB' = SB, SC' = SC. Biết rằng . Lựa chọn phương án đúng.
Cho hình chóp S.ABCD thể tích V với đáy ABCD là hình bình hành. Gọi E, F lần lượt là trung điểm của các cạnh AB và AD. Thể tích của khối chóp là
Cho hình chóp S.ABC có đáy ABC là một tam giác vuông tại A, BC = 2a, . Gọi M là trung điểm của BC. Biết SA = SM = SB = Khoảng cách từ S đến mặt phẳng (ABC)
Cho tứ diện ABCD. M, N lần lượt là trung điểm của AB và BC, P là điểm trên cạnh CD sao cho CP = 2PD. Mặt phẳng (MNP) cắt AD tại Q. Tính tỷ số .
Cho hình chóp S.ABC có ; SA = 2, SB = 3, SC = 6. Tính thể tích khối chóp S.ABC