Bài tập Hình học không gian cơ bản, nâng cao có lời giải (P6)
-
5874 lượt thi
-
30 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho hình chóp S.ABC có (SAB), (SAC) cùng vuông góc vưới mặt phẳng đáy, cạnh bên SB tạo với đáy một góc . Đáy ABC là tam giác vuông cân tại B với Gọi M, N lần lượt là trung điểm của SB, SC. Tính thể tích của khối đa diện ABMNC
 Xem đáp án
Xem đáp án
Đáp án D
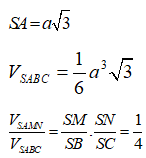
![]()
![]()

Câu 2:
Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = 3a, BC = 4a, SA = 12a và SA vuông góc với đáy. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD
 Xem đáp án
Xem đáp án
Đáp án C
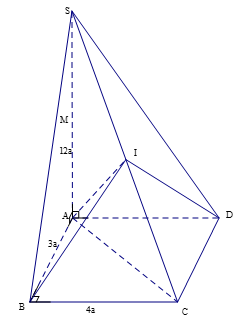
Gọi I là trung điểm SC
Tam giác SAC vuông tại A, ta có: IA = IS = IC
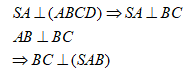
=> SBC vuông tại B, ta có IB = IS = IC
Tương tự ta có ID = IS = IC
Vậy I là tâm mặt cầu ngoại tiếp hình chóp và bán kính bằng SC
Tam giác ABC vuông tại B, ta có: AC = ![]()
Tam giác SAC vuông tại A, ta có SC = ![]()
Vậy bán kính đường tròn ngoại tiếp hình chóp là: R =
Câu 3:
Một hình trụ có diện tích xung quanh là thiết diện qua trục là hình vuông. Một mặt phẳng () song song vưới trục, cắt hình trụ theo thiết diện ABB’A’, biết một cạnh của thiết diện là một dây của đường tròn đáy hình trụ và căng một cung . Diện tích thiết diện ABB’A’ là
 Xem đáp án
Xem đáp án
Đáp án B
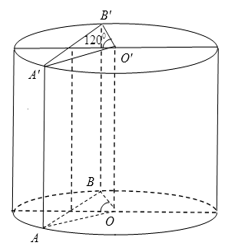
Lời giải
Vì thiết diện qua trục là hình vuông suy ra 2R = h
Ta có ![]()
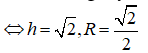
Xét tam giác OAB ta có
![]()
![]()
![]()
Vậy diện tích thiết diện là ![]()
Câu 4:
Cho hình chóp tam giác S.ABC có M, N lần lượt là trung điểm của các cạnh SA và SB. Tỉ số là:
 Xem đáp án
Xem đáp án
Đáp án D
Theo công thức tỉ lệ tứ diện, ta có:
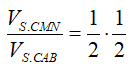
Câu 5:
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 2AD = 3AA' = 6a. Thể tích của khối hộp chữ nhật ABCD.A'B'C'D' là:
 Xem đáp án
Xem đáp án
Đáp án A
Câu 6:
Cho hình tứ diện ABCD có DA = BC = 5, AB = 3, AC = 4. Biết DA vuông góc với mặt phẳng (ABC). Thể tích của khối tứ diện ABCD là:
 Xem đáp án
Xem đáp án
Đáp án A
Dễ thấy ∆ABC vuông tại A => SABC = 6
=> VS.ABC = .6.5 = 10
Câu 7:
Cho hai vị trí A, B cách nhau 615m, cùng nằm về một phía bờ song như hình vẽ. Khoảng cách từ A và từ B đến bờ sông lần lượt là 118m và 478m . Một người đi từ A đến bờ sông để lấy nước mang về B . Đoạn đường ngắn nhất mà người đó có thể đi là
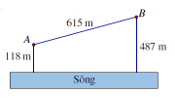
 Xem đáp án
Xem đáp án
Đáp án C

Cách 1: Giải bằng hàm số
Đặt CM = x (x > 0)
Dễ tính ra CD ![]()
Từ đề bài ta có: f (x) = ![]()
Quãng đường ngắn nhất người đó có thể đi
Giá trị nhỏ nhất của f(x) trên (0;492)
Ta có: f’(x) = 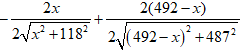
=> f’(x) = 0
![]()
![]()
![]()
![]()
![]()
Ta có bảng biến thiên
|
x |
0 |
0 |
492 |
|
y’ |
|
+ 0 - |
|
|
y |
779,8 |
||
Vậy quãng đường ngắn nhất mà người đó có thể đi là: 779,8
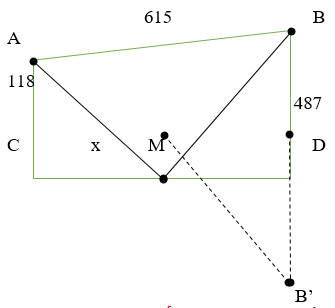
Cách 2: Giải bằng hình học
Gọi B’ là điểm đối xứng của B qua D
Dễ thấy AM + MB = AM + MB’
AM + MB ngắn nhất
AM + MB’ ngắn nhất
Dễ thấy theo bất đẳng thức tam giác: AM + MB’ ≥ AB’
AM + MB’ ngắn nhất ó AM + MB’ = AB’
Dấu “=” xảy ra khi và chỉ khi A, M, B’ thẳng hàng
Câu 9:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và SA(ABCD). Thể tích của khối chóp S.ABC là
 Xem đáp án
Xem đáp án
Đáp án B
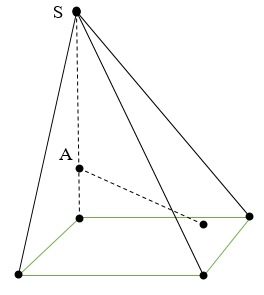
Dễ dàng tính được
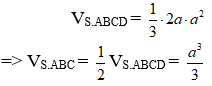
Câu 10:
Cho hình chóp S.ABCD thể tích V với đáy ABCD là hình bình hành. Gọi E, F lần lượt là trung điểm của các cạnh AB và AD. Thể tích của khối chóp là
 Xem đáp án
Xem đáp án
Đáp án A
Dễ thấy SAEC = SABC = SABCD
=> SAECF = SABCD
VS.AECF = VS.ABC
Câu 11:
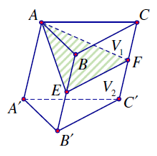
Cho hình lăng trụ ABC.A'B'C'. Gọi E, F lần lượt là trung điểm của BB' và CC'. Mặt phẳng (AEF) chia khối lăng trụ thành hai phần có thể tích và như hình vẽ. Tỉ số là
 Xem đáp án
Xem đáp án
Đáp án C
Dễ thấy VA.BCC’B’ = VABC.A’B’C’
Lại có VA.BCFE = VA.BCC’B’
=> VA.BCFE = . VABC.A’B’C’
Câu 12:
Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật, AB = a, AD = a. Biết SAABCD và góc giữa đường thẳng SC với mặt phẳng đáy bằng . Thể tích khối chóp S. ABCD bằng:
 Xem đáp án
Xem đáp án
Đáp án D
Dễ thấy ![]()
Lại có ∆SAC vuông tại A
=> AC = SA = ![]()
Vậy VS.ABCD = ![]()
Câu 13:
Thể tích khối tứ diện đều cạnh a là:
 Xem đáp án
Xem đáp án
Đáp án C
Gọi O là trọng tâm ∆ABC
Kẻ BH AC
Vì SABC là tứ diện đều => SO(ABC)
Vì ∆ABC đều ![]()
Xét ∆SBO vuông tại O
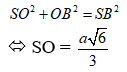
VS.ABC = ![]()
Câu 15:
Cho tứ diện đều ABCD cạnh bằng a. Khoảng cách d giữa hai đường thẳng AD và BC là:
 Xem đáp án
Xem đáp án
Đáp án B
Gọi O là trọng tâm ∆ABC
Kẻ AM AC và MH AD
Vì DABC là tứ diện đều => DO(ABC)
Vì ∆ABC đều => AO = ![]()
Xét ∆DAO vuông tại O

Ta có: DO BC và AMBC
=> (DAM)BC
=> MH BC
Lại có MHDA
=> MH = d(BC, DA)
Xét ∆DAM, ta có:
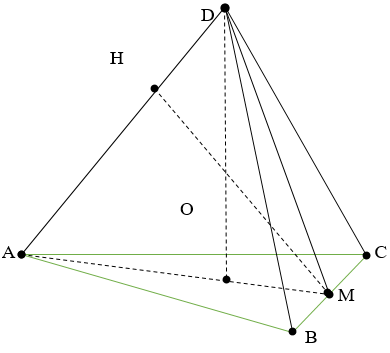
DO.AM = MH.AD
MH =
d(BC, DA) =
Câu 16:
Cho hình chóp tứ giác S.ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh SA, SB, SC, SD. Tỉ số là là:
 Xem đáp án
Xem đáp án
Đáp án A
Theo công thức tỉ lệ tứ diện, ta có:
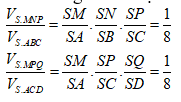
Theo dãy tỉ số bằng nhau ta có
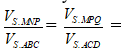
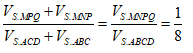
Câu 18:
Thiết diện của một mặt phẳng với một tứ diện chỉ có thể là:
 Xem đáp án
Xem đáp án
Đáp án C
Đó là các mặt phẳng: Qua S và song song với (ABCD); qua S và trung điểm của các cạnh AB và CD; qua S và trung điểm của các cạnh AD và CB;
Câu 19:
Cho hình chóp tứ giác đều S.ABCD. Số mặt phẳng qua điểm S cách đều các điểm A,B,C,D là:
 Xem đáp án
Xem đáp án
Đáp án C.
Câu 20:
Cho hình chóp S.ABC có đáy ABC là một tam giác vuông tại A, BC = 2a, . Gọi M là trung điểm của BC. Biết SA = SM = SB = Khoảng cách từ S đến mặt phẳng (ABC)
 Xem đáp án
Xem đáp án
Đáp án A

AMB là tam giác đều cạnh a (vì AM = MB = a và )
Gọi H là chân đường cao hạ từ S xuống (ABC). Do SA = SB = SM nên H trùng với trọng tâm tam giác AMB.
Ta có 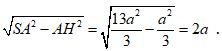
Vậy SH = 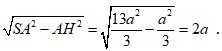
Câu 22:
Khối đa diện đều nào sau đây có số đỉnh nhiều nhất?
 Xem đáp án
Xem đáp án
Đáp án B
Số đỉnh của khối nhị thập diện đều là 20.
Câu 25:
Cắt hình chóp tứ giác bởi mặt phẳng vuông góc với đường cao của hình chóp thiết diện là hình gì?
 Xem đáp án
Xem đáp án
Đáp án C
Câu 26:
Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng . Tính khoảng cách giữa hai đường thẳng AB' và A'C'
 Xem đáp án
Xem đáp án
Đáp án A.
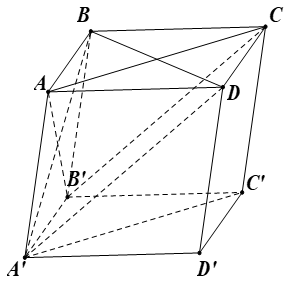
Ta có AA'BC là chóp đều có tất cả các cạnh bằng 1
![]()
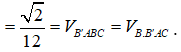
Ta có ![]()
![]()
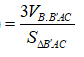
Lại có AB'C có B'C = A'D = 1; ![]() (do là hình thoi cạnh 1 có )
(do là hình thoi cạnh 1 có )
Do đó
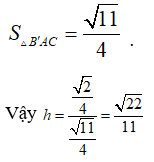
Câu 27:
Cho hình chóp S.ABC có ; SA = 2, SB = 3, SC = 6. Tính thể tích khối chóp S.ABC
 Xem đáp án
Xem đáp án
Đáp án D
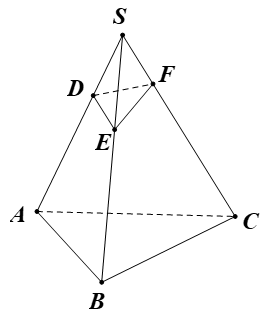
Gọi D, E, F lần lượt trên SA, SB, SC sao cho SD = SE = SF = 1 => S.DEF là hình chóp đều cạnh a
Ta có 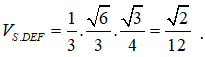
Lại có 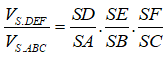
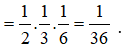
Vậy 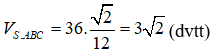
Câu 28:
Cho tứ diện ABCD. M, N lần lượt là trung điểm của AB và BC, P là điểm trên cạnh CD sao cho CP = 2PD. Mặt phẳng (MNP) cắt AD tại Q. Tính tỷ số .
 Xem đáp án
Xem đáp án
Đáp án A
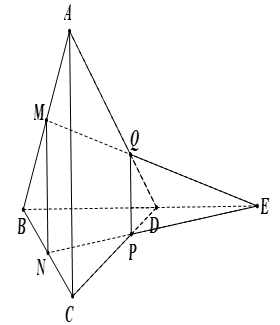
Gọi ![]() thì Q là giao điểm của (MNP) và AD.
thì Q là giao điểm của (MNP) và AD.
Áp dụng định lí Menelaus trong ta có:
![]()
![]()
Áp dụng định lí Menelaus trong ABD ta có:
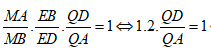
![]()
Câu 29:
Cho hình chóp S.ABC, trên các cạnh SA, SB, SC lần lượt lấy các điểm A', B', C' sao cho SA' = SA, SB' = SB, SC' = SC. Biết rằng . Lựa chọn phương án đúng.
 Xem đáp án
Xem đáp án
Đáp án là D
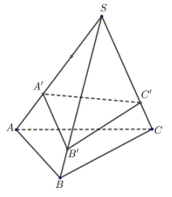
Ta có 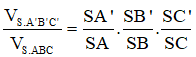
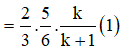
Theo giả thiết 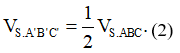
Từ (1) và (2) suy ra ![]()