30 câu hỏi trắc nghiệm thuộc Bài tập Hình học không gian cơ bản, nâng cao có lời giải (P12)

Câu 1:

Tứ diện OABC, có OA = a, OB = b, OC = c và đôi một vuông góc với nhau. Thể tích khối tứ diện OABC bằng

$A . \frac{a b c}{3}$

$B . a b c$

$C . \frac{a b c}{6}$

$D . \frac{a b c}{2}$

Xem đáp án

Đáp án C

Câu 2:

Một khối chóp có thể tích bằng $\frac{a^{3} \sqrt{6}}{3}$ và chiều cao bằng 2a. Diện tích mặt đáy của khối chóp là

$A . B = \frac{\sqrt{6} a^{2}}{2}$

$B . B = \frac{\sqrt{6} a}{2}$

$C . B = \frac{\sqrt{6} a}{4}$

$D . B = \sqrt{6} a$

Xem đáp án

Đáp án A

Câu 3:

Tính thể tích của khối lập phương ABCD.A'B'C'D' biết AD' = 2a

A. V = $a^{3}$

B. V = 8 $a^{3}$

C. V = $2 \sqrt{2}$ $a^{3}$

D. V = $\frac{2 \sqrt{2}}{3}$ $a^{3}$

Xem đáp án

Đáp án C

Ta có

Vậy cạnh của hình lập phương trình có cạnh độ dài $\sqrt{2}$ a.

Vậy

Câu 4:

Cho khối hộp ABCD.A'B'C'D'. Mặt phẳng (P) đi qua trung điểm của AB, A'D' và CC' chia khối hộp thành hai đa diện. Khối chứa đỉnh D có thể tích là $V_{1}$ , khối chứa đỉnh B có thể tích là $V_{2}$ Khi đó ta có

$A . \frac{V_{1}}{V_{2}} = \frac{1}{2}$

$B . \frac{V_{1}}{V_{2}} = \frac{3}{4}$

$C . \frac{V_{1}}{V_{2}} = 1$

$D \frac{V_{1}}{V_{2}} = \frac{1}{3}$

Xem đáp án

Đáp án C

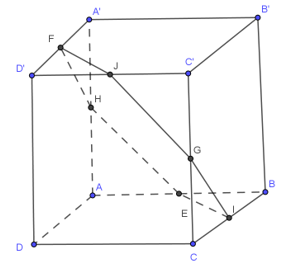
Ta thấy rằng mặt phẳng đi qua tâm của hình hộp I, nên do đó nó chia hình thành 2 hình có thể tích bằng nhau. Tức là $\frac{V_{1}}{V_{2}} = 1$

Câu 5:

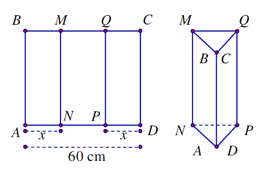
Cho môt tấm tôn hình chữ: nhật ABCD có AD = 60 cm. Ta gấp tấm tôn theo 2 cạnh MN và QP vào phía trong sao cho BA trùng với CD(như hình vẽ) để được lăng trụ đứng khuyết hai đáy. Khối lăng trụ có thể tích lớn nhất khi x bằng bao nhiêu?

A. x = 20

B. x = 30

C. x = 45

D. x = 40

Xem đáp án

Đáp án A

Thể tích lớn nhất khi diện tích tam giác NPD là lớn nhất, điều này xảy ra khi tam giác đó là tam giác đều (vì chu vi là không đổi) tức là x = 20 cm

Câu 6:

Cho tứ diện ABCD có các cạnh BA, BC, BC đôi một vuông góc với nhau, BA = 3a, BC = BD = 2a. Gọi M và N lần lượt là trung điểm của AB và AD. Tính thể tích khối chóp C.BDNM

A. V = 8 $a^{3}$

B. V = $\frac{2 a^{3}}{3}$

C. V = $\frac{3 a^{3}}{2}$

D. V = $a^{3}$

Xem đáp án

Đáp án C

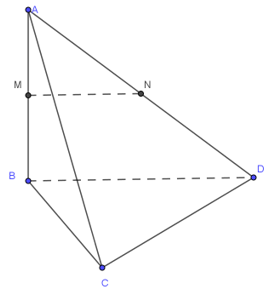
Ta có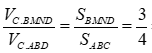

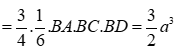
Câu 7:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm H thuộc cạnh AB sao cho HB = 2HA. Cạnh SC tạo với mặt phẳng đáy (ABCD) một góc bằng $60^{0}$ . Khoảng cách từ trung điểm K của HC đến mặt phẳng (SCD) là

$A . \frac{a \sqrt{13}}{2}$

$B . \frac{a \sqrt{13}}{4}$

$C . a \sqrt{13}$

$D . \frac{a \sqrt{13}}{8}$

Xem đáp án

Đáp án B

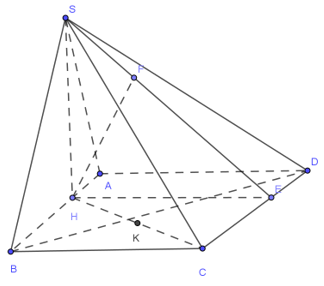
Ta có d(K;(SCD))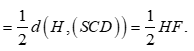

Ta có

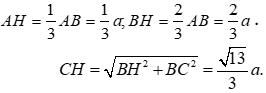
Có góc giữa SC và đáy là nên ta có

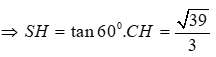
Ta có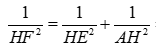

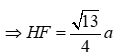
Câu 8:

Hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D; biết AB = AD = 2a, CD = a. Gọi I là trung điểm của AD, biết hai mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt phẳng (ABCD), Thể tích khối chóp S.ABCD bằng $\frac{3 \sqrt{15} a^{3}}{5}$ . Góc giữa hai mặt phẳng (SBC) và (ABcD) bằng

$A . 90^{0}$

$B . 60^{0}$

$C . 30^{0}$

$D . 45^{0}$

Xem đáp án

Đáp án B

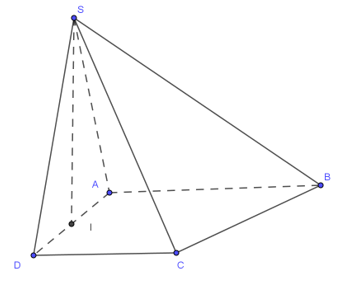
Kẻ IH $⊥$ BC. Ta có:

Mà

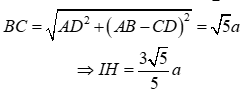
Dễ thấy góc giữa 2 mặt phẳng (SBC) và (ABCD) là góc SJI, có:

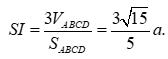
Vậy

Câu 9:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy, SA = a. Gọi M là trung điểm của CD. Khoảng cách từ M đến mặt phẳng (SAB) là:

$A . \frac{a \sqrt{2}}{2}$

$B . a$

$C . a \sqrt{2}$

$D . 2 a$

Xem đáp án

Đáp án B

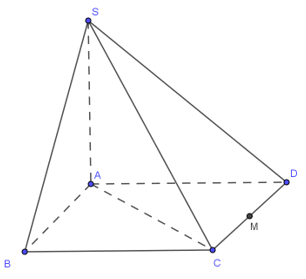
d(M;(SAB)) = d(D;(SAB)) = DA = a

Câu 10:

Cho hình chóp S.ABCD đáy là hình thang vuông tại A và B, AB = BC = a, AD = 2a, SA vuông góc với đáy, SA = a. Gọi M, N lần lượt là trung điểm của SB, CD. Tính côsin góc giữa MN và (SAC)

$A . \frac{1}{\sqrt{5}}$

$B . \frac{3 \sqrt{5}}{10}$

$C . \frac{\sqrt{55}}{10}$

$D . \frac{2}{\sqrt{5}}$

Xem đáp án

Đáp án C

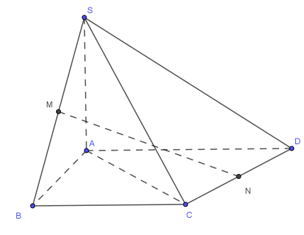
Kẻ CN $⊥$ AB ta dễ dàng tính được

=> tam giác ADC vuông tại C. Từ đó NC $⊥$ (SAC)

Gọi O là trung điểm của AC, dễ dàng cm được BD $⊥$ (SAC)

=> MK $⊥$ (SAC). vơí K là trung điểm của SO, từ đó KC là hc của MN lên .

Ta kẻ KZ $⊥$ AC

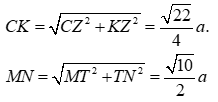
với T là trung điểm của AB.

Gọi $α$ là góc tạo với MN và (SAC)

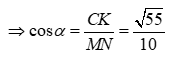
Câu 11:

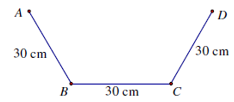
Từ một tấm tôn có kích thước 90cm x 3m, người ta làm một máng xối nước trong đó mặt cắt là hình thang ABCD có hình dưới. Tính thể tích lớn nhất của máng xối.

$A . 40500 \sqrt{6} c m^{3}$

$B . 40500 \sqrt{5} c m^{3}$

$C . 202500 \sqrt{3} c m^{3}$

$D . 40500 \sqrt{2} c m^{3}$

Xem đáp án

Đáp án C

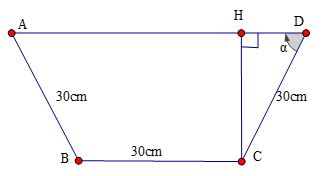
Ta có:

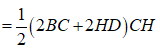
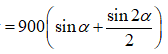
Xét hàm số:

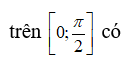
dễ thấy

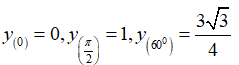
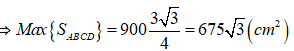
Vậy thể tích lớn nhất của máng xối là:

Câu 12:

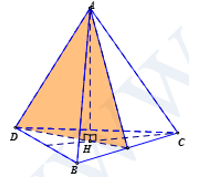
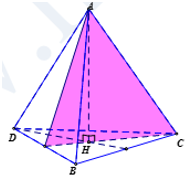
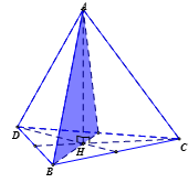
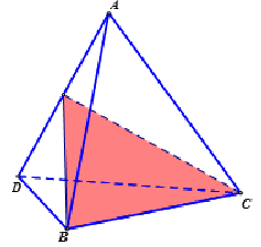
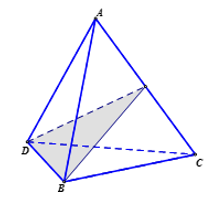
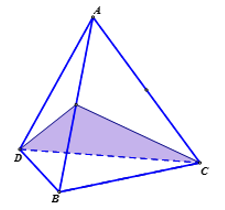
Tìm số mặt phẳng đối xứng của tứ diện đều.

A. 4

B. 9

C. 3

D. 6

Xem đáp án

Đáp án D

Hình tứ diện đều có 6 mặt phẳng đối xứng

Câu 13:

Cho hình lăng trụ đứng ABC.A'B'C'. Cạnh bên AA' = a, ABC là tam giác vuông tại A có BC = 2a, AB = a $\sqrt{3}$ . Tính khoảng cách từ đỉnh A đến mặt phẳng (A'BC)

$A . \frac{a \sqrt{21}}{7}$

$B . \frac{a \sqrt{21}}{21}$

$C . \frac{a \sqrt{3}}{7}$

$D . \frac{a \sqrt{7}}{21}$

Xem đáp án

Đáp án A

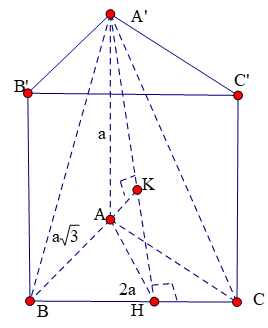
Kẻ đường cao AH của tam giác ABC khi đó BC $⊥$ A'AH, trong $∆$ A'AH kẻ đường cao AK thì

AK $⊥$ (A'BC), ta có:

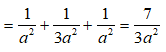
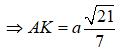
Câu 14:

Cho hình chóp tam giác S.ABC có $\hat{A S C} = \hat{C S B} = 60^{0}, \hat{A C S} = 90^{0}$ , SA = SB = a, SC = 3a. Tính thể tích của khối chóp ?

$A . \frac{a^{3} \sqrt{2}}{8}$

$B . \frac{a^{3} \sqrt{2}}{4}$

$C . \frac{a^{3} \sqrt{2}}{12}$

$D . \frac{a^{3} \sqrt{2}}{3}$

Xem đáp án

Đáp án B

Công thức tính thể tích hình chóp tam giác biết độ dài các cạnh bên a, b, c và các góc tạo bởi các cạnh bên là $α, β, γ$ như sau:

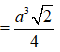
Câu 15:

Cho khối chóp tam giác đều S.ABC có thể tích là $a^{3}$ , AB = a. Tính theo a khoảng cách từ S tới mặt phẳng (ABC)

$A . 2 a \sqrt{3}$

$C . 4 a \sqrt{6}$

$D . a \sqrt{3}$

Xem đáp án

Đáp án B

Diện tích tam giác đều có cạnh là a bằng $a^{2} \frac{\sqrt{3}}{4}$

=> khoảng cách từ S tới (ABC)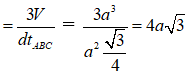

Câu 16:

Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích bằng 1. Trên cạnh SC lấy điểm E sao cho SE = 2EC. Tính thể tích V của khối tứ diện SEBD.

A. V = $\frac{2}{3}$

B. V = $\frac{1}{6}$

C. V = $\frac{1}{3}$

D. V = $\frac{4}{3}$

Xem đáp án

Đáp án C

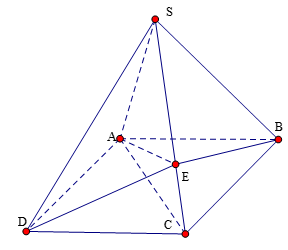
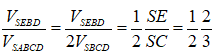
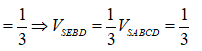
Câu 17:

Trong các mặt của khối đa diện, số cạnh cùng thuộc một mặt tối thiểu là

A. 5

B. 4

C. 3

D. 2

Xem đáp án

Đáp án C

Khối đa diện có các mặt là các đa giác có số cạnh tối thiểu là ba

Câu 18:

Cho lăng trụ tứ giác đều có tất cả các cạnh bằng nhau và biết tổng diện tích các mặt của lăng trụ bằng 296cm . Tính thể tích khối lăng trụ.

A. 128 $c m^{2}$

B. 64 $c m^{2}$

C. 32 $c m^{2}$

D. 60 $c m^{2}$

Xem đáp án

Đáp án B

Hình lăng trụ tứ giác đều có tất cả các cạnh bằng nhau là hình lập phương.

Gọi a là độ dài một cạch thì tổng diện tích các mặt S = 6 $a^{2}$ => a = 4.

=> thể tích lăng trụ là V = $a^{3} = 4^{3}$ = 64

Câu 19:

Các trung điểm của tất cả các cạnh của hình tứ diện đều là các đỉnh của

A. Hình lập phương.

B. Hình bát diện đều.

C. Hình tứ diện đều.

D. Hình hộp chữ nhật.

Xem đáp án

Đáp án C

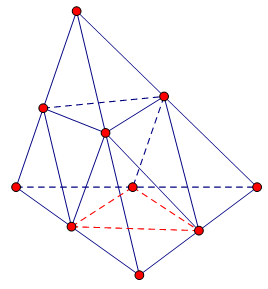
Tứ diện đều có 6 cạnh tương ứng có 6 trung điểm là các đỉnh của hình bát diện đều.

Câu 20:

Hình nào dưới đây không phải là hình đa diện ?

A. Hình trụ.

B. Hình lập phương.

C. Hình chóp.

D. Hình bát diện đều.

Xem đáp án

Đáp án A

Hình trụ không phải hình đa diện mà là hình tròn xoay.

Câu 21:

Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = a, BC = a $\sqrt{3}$ , biết SA = a và vuông góc với mặt phẳng đáy. Một mặt phẳng ( $α$ ) đi qua A , vuông góc với SC tại H , cắt SB tại K . Tính thể tích khối chóp S.AHK theo a

$A . \frac{a^{3} \sqrt{3}}{30}$

$B . \frac{5 a^{3} \sqrt{3}}{60}$

$C . \frac{a^{3} \sqrt{3}}{60}$

$D . \frac{a^{3} \sqrt{3}}{10}$

Xem đáp án

Đáp án C

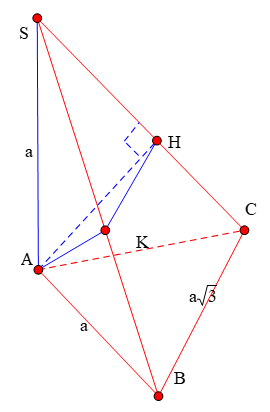
Ta có AC =

SC =

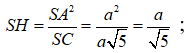
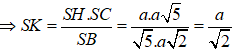
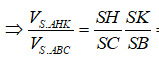
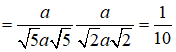
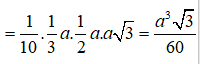
Câu 22:

Phát biểu nào sau đây là đúng?

A. Hình hai mươi mặt đều có 20 đỉnh, 30 cạnh, 12 mặt

B. Hình hai mươi mặt đều có 30 đỉnh, 12 cạnh, 20 mặt.

C. Hình hai mươi mặt đều có 30 đỉnh, 20 cạnh, 12 mặt.

D. Hình hai mươi mặt đều có 12 đỉnh, 30 cạnh, 20 mặt.

Xem đáp án

Đáp án D

Hình hai mươi mặt đều có 12 đỉnh, 30 cạnh, 20 mặt.

Câu 23:

Cho hình chóp tứ giác đều S.ABCD, có cạnh đáy bằng a và thể tích khối chóp bằng $\frac{a^{3} \sqrt{2}}{6}$ . Tính theo a khoảng cách từ điểm A đến mặt phẳng (SBC)

$A . \frac{a \sqrt{6}}{2}$

$B . \frac{a \sqrt{6}}{3}$

$C . \frac{a \sqrt{6}}{6}$

$D . a \sqrt{6}$

Xem đáp án

Đáp án B

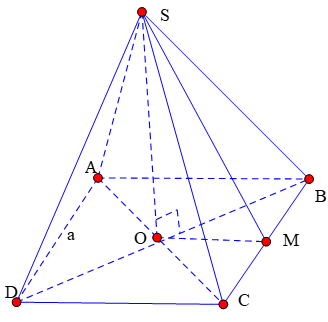
Gọi M là trung điểm BC; Gọi d là khoảng cách từ A tới (SBC)

Ta có:

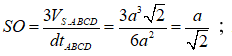
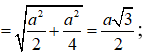
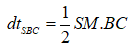
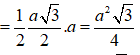
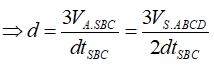
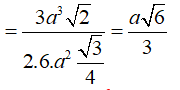
Câu 24:

Thể tích khối tứ diện đều ABCD có cạnh bằng $\sqrt{2}$ là:

A. V = $\frac{1}{12}$

B. V = $\frac{\sqrt{2}}{3}$

C. V = $\frac{1}{6}$

D. V = $\frac{1}{3}$

Xem đáp án

Đáp án D

Ta tính trên trường hợp tổng quát tứ diện ABCD đều cạnh a

với là trực tâm tam giác đều ABC

Ta có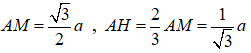

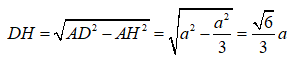
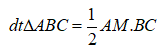
Như vậy

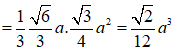
Câu 25:

Tính tổng diện tích các mặt của một khối bát diện đều cạnh a .

$A . 2 a^{3} \sqrt{3}$

$B . \frac{a^{3} \sqrt{3}}{16}$

$C . 8 a^{2} \sqrt{3}$

$D . 8 a^{2}$

Xem đáp án

Đáp án C

Diện tích của tam giác đều có cạnh là a bằng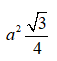

Ta có: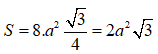

Câu 26:

Hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 3cm, BC = 4 cm, SC = 5 cm. Tam giác SAC nhọn và nằm trong mặt phẳng vuông góc với (ABCD). Các mặt (SAB) và (SAC) tạo với nhau một góc $α$ sao cho $α$ = $\frac{3}{29}$ . Tính thể tích khối chóp S.ABCD

$A . 16 c m^{2}$

$B . 15 \sqrt{29} c m^{2}$

$C . 20 c m^{2}$

$D . 18 \sqrt{5} c m^{2}$

Xem đáp án

Đáp án A

Gọi chiều cao của hình chóp là h => h < SC = 5 cm

Câu 27:

Tính thể tích khối lập phương ABCD.A'B'C'D' biết độ dài đoạn thẳng AC = 2a.

$A . \frac{2 a^{3} \sqrt{2}}{3}$

$B . 2 a^{3} \sqrt{2}$

$C . a^{3}$

$D . \frac{a^{3}}{3}$

Xem đáp án

Đáp án B

Ta có AC = 2a => cạnh của hình lập phương là $\sqrt{2}$ a

Câu 28:

Trong các mệnh đề sau, mệnh đề nào sai?

A. Nếu hai mặt phẳng có một điểm chung thì chúng còn có vô số các điểm chung khác nữa.

B. Nếu hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì chúng song song với nhau.

C. Nếu một đường thẳng cắt một trong hai mặt phẳng song song với nhau thì cắt mặt phẳng còn lại.

D. Nếu hai đường thẳng phân biệt cùng song song với một mặt phẳng thì chúng song song với nhau.

Xem đáp án

Đáp án D

Hai đường thẳng song song với mặt phẳng có thể cắt nhau hoặc chéo nhau

Câu 29:

Một khối đa diện lồi với các mặt là tam giác thì:

A. 3M = 2C

B. 3M > 2C

C. 3M < 2C

D. cả 3 đáp án sai

Xem đáp án

Đáp án A

Một mặt có 3 cạnh, và mỗi cạnh là cạnh chung của 2 mặt nên ta có đáp án A đúng

Câu 30:

Trong các mệnh đề sau, mệnh đề nào sai?

A. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

B. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì cũng vuông góc với đường thẳng còn lại.

C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

D. Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng vuông góc với một đường thẳng thì song song với nhau.

Xem đáp án

Đáp án C

Đáp án C sai vì hai mặt phẳng cùng vuông góc với một mặt phẳng có thể cắt nhau