Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, AB = 8a, AC = 6a, hình chiếu của A’ trên (ABC) trùng với trung điểm của BC, AA' = 10a. Thể tích khối lăng trụ ABC.A’B’C’ là
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án là A
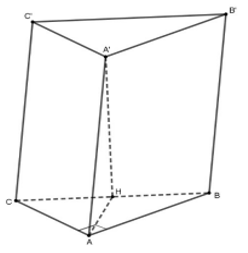
Gọi H là trung điểm BC. Ta có ![]()
Tam giác AHA’ vuông tại H nên: ![]()
![]()
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a , góc giữa cạnh bên và đáy bằng . Thể tích khối chóp S.ABC là
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AB = 2a, BC = CD = AD = a. Gọi M là trung điểm của AB. Biết SC = SD = SM và góc giữa cạnh bên SA và mặt phẳng đáy (ABCD) là . Thể tích hình chóp đó là:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác đều cạnh 2a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết rằng mặt phẳng (SBC) tạo với mặt phẳng đáy một góc
Cho các hình khối sau:
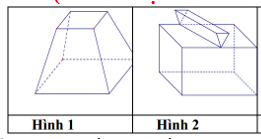
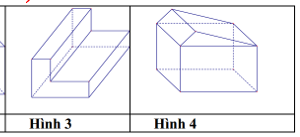
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số đa diện lồi là:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Biết SA vuông góc với mặt phẳng đáy và SB = a, BC = 2a, SC = 2a. Thể tích khối chóp S.ABC là:
Cho hình chóp có thể tích V, diện tích mặt đáy là S. Chiều cao tương ứng của hình chóp
Cho hình chóp tứ giác có đáy là hình vuông. Biết chiều cao và thể tích của chóp lần lượt bằng 3cm và 12 . Độ dài cạnh đáy của hình chóp đó tính theo đơn vị cm là:
Cho hình lăng trụ ABC.A’B’C’, trên các cạnh AA’, BB’ lấy các điểm M, N sao cho AA' = 4A'M, BB' = 4B'N. Mặt phẳng (C'MN) chia khối lăng trụ thành hai phần. Gọi là thể tích khối chóp C’.A’B’MN và là thể tích khối đa diện ABCMNC’. Tính tỷ số
Cho khối lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a và điểm A’ cách đều ba điểm A, B, C. Cạnh bên AA’ tạo với mặt phẳng đáy một góc . Tính thể tích khối lăng trụ ABC.A’B’C’
Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D'. Biết AC = 2a và cạnh bên AA' = a Thể tích lăng trụ đó là:
Cho hình hộp ABCD.A'B'C'D' có O là giao điểm của AC và BD. Tỷ số thể tích của hình hộp đó và hình chóp O.A'B'D' là: