Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Điểm M thuộc đoạn thẳng BC' , điểm N thuộc đoạn thẳng AB' tạo với mặt phẳng đáy một góc . Tìm độ dài nhỏ nhất của đoạn thẳng MN.
Giải bởi Vietjack
Đáp án D
Ý tưởng: 1 - MN phải chăng sẽ là hai điểm đặc biệt nào đó
2 – Khi nhận ra M là trung điểm của BA’ thì ta tiến hành tính toán MN qua điểm A’ bằng cách lấy P thuộc BC’!
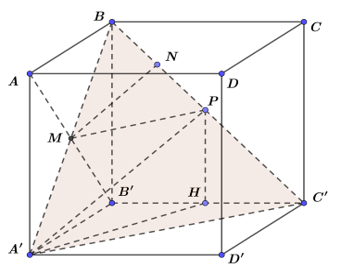
Lời giải: Dễ có mặt phẳng (BA’C’) vuông góc với AB’. Do đó để MN là nhỏ nhất thì M là giao của AB’ và BA’, N là điểm thuộc BC’ sao cho góc giữa MN và (A’B’C’D’) là . Gọi P là điểm thuộc BC’sao cho A’P cũng hợp với mặt phẳng đáy một góc , khi đó MN là đường trung bình của tam giác BA’P nên MN = A'P.
Giả sử độ dài đoạn B’H = x, khi đó PH = HC’ = a – x (tam giác PC’H vuông cân tại C’), và A'H = 
Theo điều ta đã giả sử ở trên thì góc giữa A’P và (A’B’C’D’) = , do đó
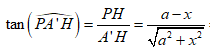
Mặt khác ta lại có A'P = 
(2)
Từ (1) và (2) ta tính được 
Từ đây ta rút ra được
=> Chọn phương án D.
Cho lăng trụ đứng ABCD.A'B'C'D' có đáy là hình bình hành. Các đường chéo DB' và AC' lần lượt tạo với đáy các góc. Biết chiều cao của lăng trụ là a và , hãy tính thể tích V của khối lăng trụ này.
Tính thể tích của một khối lăng trụ tam giác đều ABC.A'B'C' có AC' bằng 5a, đáy là tam giác đều cạnh bằng 4a
Cho một tấm nhôm hình vuông cạnh 1 (m) như hình vẽ dưới đây. Người ta cắt phần tô đậm của tấm nhôm rồi gập thành một hình chóp tứ giác đều có cạnh đáy bằng x (m). Tìm giá trị của x để khối chóp nhận được có thể tích lớn nhất.
Tính thể tích khối chóp tứ giác đều có cạnh đáy bằng 2a và diện tích của một mặt bên là
Cho tứ diện đều ABCD có cạnh bằng a. Tính khoảng cách từ đỉnh B đến mặt phẳng (ACD).
Cho hình chóp S.ABCD có cạnh SA = x còn tất cả các cạnh khác có độ dài bằng 2. Tính thể tích lớn nhất của khối chóp S.ABCD
Cho hình nón tròn xoay có đường cao là a, đường kính đáy là 2a. Tìm diện tích xung quanh của hình nón đã cho.
Cho tứ diện SABC có ABC là tam giác vuông cân tại A, đường cao SA. Biết đường cao AH của tam giác ABC bằng a, góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) bằng .Tính theo a thể tích khối tứ diện SABC
Cho một tứ diện có đúng một cạnh có độ dài bằng x thay đổi được, các cạnh còn lại có độ dài bằng 2. Tính giá trị lớn nhất của thể tích tứ diện này.
Cho khối tứ diện ABCD có thể tích bằng V, thể tích của khối đa diện có đỉnh là trung điểm các cạnh của tứ diện ABCD bằng V'. Tính tỉ số
Cho hình trụ có bán kính đáy bằng 3 cm, độ dài đường cao bằng 4 cm. Tính diện tích xung quanh của hình trụ này.
Cho lăng trụ ABC.A'B'C' có các mặt bên là hình vuông cạnh a. Gọị D,E lần lượt là trung điểm các cạnh BC, A'C'. Tính khoảng cách giữa hai đường thẳng AB' và DE theo a
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 1. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (ABCD). Tính khoảng cách từ B đến (SCD)
Cho khối chóp S.ABC có các điểm A', B', C' lần lượt thuộc các cạnh SA, SB, SC thỏa 3SA' = SA, 4SB' = SB, 5SC' = 3SC. Biết thể tích khối chóp S.A'B'C' bằng 5 (). Tìm thể tích khối chóp S.ABC
