Cho hình bình hành ABCD (AB > AD). Gọi E và K lần lượt là trung điểm của CD và AB. BD cắt AE, AC, CK lần lượt tại N, O và I. Chứng minh rằng:
a. Tứ giắc AECK là hình bình hành.
b. Ba điểm E, O, K thẳng hàng.
c. DN = NI = IB
d. AE = 3KI
 Giải bởi Vietjack
Giải bởi Vietjack
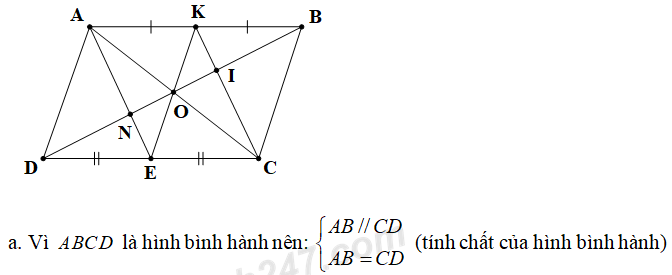
Mà E, K lần lượt là trung điểm của CD và AB nên AK = EC VÀ AK // EC.
⇒ Tứ giác AECK là hình bình hành (dấu hiệu nhận biết)
b. Trong hình bình hành ABCD có O là giao điểm của hai đường chéo nên O là trung điểm của AC và BD (tính chất của hình bình hành)
Mà AECK là hình bình hành nên O là trung điểm của EK.
⇒ Ba điểm E, O, K thẳng hàng.

Cho x, y là hai số thực tùy ý, tìm giá trị nhỏ nhất của biểu thức sau:
P = x2 + 5y2 + 4xy + 6x + 16y + 32
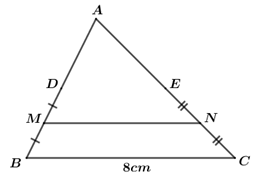
Cho tam giác ABC có cạnh BC = 8cm và D, E, M, N lần lượt là trung điểm của AB, AC, BD và CE (như hình vẽ). Khi đó, độ dài của MN là
Cho hình bình hành ABCD có ∠A = 60o. Khi đó, hệ thức nào sau đây là không đúng?
Hình chữ nhật có độ dài cạnh 5cm và 12cm thì khoảng cách từ giao điểm hai đường chéo đến mỗi đỉnh là
Rút gọn các biểu thức sau:
a. 2x(3x + 2) - 3x(2x + 3)
b. (x + 2)3 + (x - 3)2 - x2(x + 5)
c. (3x3 - 4x2 + 6x) : 3x
Giá trị biểu thức 20092 - 2018.2009 + 10092 có bao nhiêu chữ số 0 ?