A.
B.
C. .
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Cho hình lập phương ABCD.A'B'C'D' (tham khảo hình vẽ).
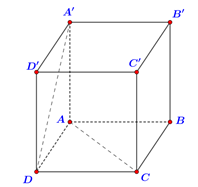
Góc giữa hai đường thẳng AC và A'D bằng
Cho tứ diện ABCD có AB = AC = AD và . Hãy xác định góc giữa cặp vectơ và .