Công thức nào sau đây là công thức tính độ dịch chuyển trong chuyển động thẳng biến đổi đều?
A. \[{\rm{d = }}{{\rm{v}}_{\rm{0}}}{\rm{.t + }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{.a}}{\rm{.}}{{\rm{t}}^{\rm{2}}}\].
B. \[{\rm{d = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{.a}}{\rm{.}}{{\rm{t}}^{\rm{2}}}\].
C. \[{\rm{d = }}{{\rm{v}}_{\rm{0}}}{\rm{.t + 2}}{\rm{.a}}{\rm{.}}{{\rm{t}}^{\rm{2}}}\].
D. \[{\rm{d = 2}}{{\rm{v}}_{\rm{0}}}{\rm{.t + a}}{\rm{.}}{{\rm{t}}^{\rm{2}}}\].
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A.
Công thức tính độ dịch chuyển trong chuyển động thẳng biến đổi đều: \[{\rm{d = }}{{\rm{v}}_{\rm{0}}}{\rm{.t + }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{.a}}{\rm{.}}{{\rm{t}}^{\rm{2}}}\]
Trong chuyển động thẳng biến đổi đều, véctơ gia tốc tức thời có đặc điểm:
Công thức vận tốc tức thời trong chuyển động thẳng biến đổi đều nếu thời điểm ban đầu \[{{\rm{t}}_{\rm{0}}} = 0\] vật mới bắt đầu chuyển động.
Đồ thị bên dưới mô tả sự thay đổi vận tốc theo thời gian trong chuyển động của một vật đang chuyển động từ A đến B. Gia tốc của ô tô từ giây thứ 20 đến giây thứ 28 là bao nhiêu?
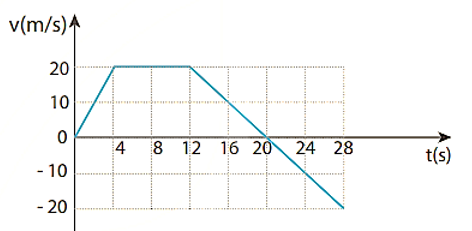
Một ô tô bắt đầu chuyển động thẳng nhanh dần đều từ trạng thái đứng yên. Trong 4 s đầu ô tô đi được đoạn đường 10 m và không đổi chiều chuyển động. Tính vận tốc của ô tô ở cuối giây thứ hai.
Đồ thị nào sau đây là đồ thị vận tốc - thời gian của chuyển động thẳng biến đổi đều?
Một đoàn tàu bắt đầu rời ga, chuyển động thẳng nhanh dần đều. Sau khi đi được 1000 m đạt đến vận tốc 10 m/s. Tính vận tốc của tàu sau khi đi được 2000 m.