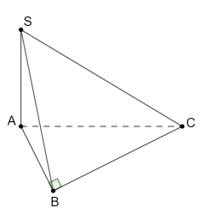
Cho hình chóp S.ABC có đáy là tam giác vuông tại B và SA ^ (ABC). Mệnh đề nào sau đây đúng?
A. Chỉ có đúng 2 mặt bên của hình chóp đã cho là các tam giác vuông;
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có:
Ta có:
+) SA ^ (ABC) Þ SA ^ AB
nên tam giác SAB vuông tại A.
+) SA ^ (ABC) Þ SA ^ AC
nên tam giác SAC vuông tại A.
+) SA ^ (ABC) Þ SA ^ CB
mà AB ^ BC nên BC ^ (SAB).
Từ đó suy ra BC ^ SB
nên tam giác SCB vuông tại B.
Vậy cả 3 mặt bên của hình chóp
đã cho là các tam giác vuông.
+) SA ^ (ABC) Þ SA ^ AB
nên tam giác SAB vuông tại A.
+) SA ^ (ABC) Þ SA ^ AC
nên tam giác SAC vuông tại A.
+) SA ^ (ABC) Þ SA ^ CB
mà AB ^ BC nên BC ^ (SAB).
Từ đó suy ra BC ^ SB
nên tam giác SCB vuông tại B.
Vậy cả 3 mặt bên của hình chóp
đã cho là các tam giác vuông.
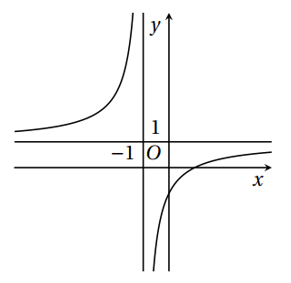
Hàm số y = f (x) có đồ thị như hình bên. Hàm số gián đoạn tại điểm có hoành độ bằng bao nhiêu?
Cho tứ diện đều ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB và BC. Tính số đo góc giữa hai đường thẳng MN và CD.
Cho hình chóp S.ABCD có SA vuông góc với đáy và SA = 1, đáy là hình vuông cạnh x (0 < x £ 1). Tính giá trị lớn nhất của diện tích thiết diện của hình chóp đã cho khi cắt bởi mặt phẳng đi qua A và vuông góc với SC.
Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Khẳng định nào sau đây đúng?
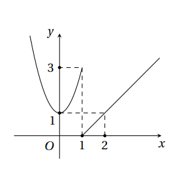
Hình vẽ sau là đồ thị của một hàm số y = f (x). Hãy quan sát đồ thị và cho biết lần lượt có giá trị bằng