 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
Phương trình mặt phẳng (P) có vectơ chỉ phương là →AB=(−1;−2;3)
Vectơ pháp tuyến của mặt phẳng (P) là →n=(A; B; C) sao cho:
→n.→AB=0⇔ (–1).A + (–2).B + 3.C = 0
⇔A = 3C – 2B ⇒→n=(3C−2B; B; C)
Mặt phẳng (P) đi qua A(1; 0; 0) và có Vectơ pháp tuyến là →n=(3C−2B; B; C) có dạng:
(3C – 2B).(x – 1) + By + Cz = 0
⇔(3C – 2B).x + By + Cz + 2B – 3C = 0
Khoảng cách từ C(1; 1; 1) đến (P) là d với:
d=|(3C−2B).1+B.1+C.1+2B−3C|√(3C−2B)2+B2+C2
=|B+C|√5B2−12BC+10C2
+ Với C = 0 ⇒d=1√5 (loại)
+ Với C ≠ 0 ⇒d=|BC+1|√5(BC)2−12(BC)+10
Đặt t=BC (t > 0)
Ta có: d=|t+1|√5t2−12t+10=2√3
Bình phương hai vế, ta được:
3|t + 1|2 = 4(5t2 – 12t + 10)
⇔ 3.(t2 + 2t + 1) = 4.(5t2 – 12t + 10)
⇔ 3t2 + 6t + 3 = 20t2 – 48t + 40
⇔17t2 – 54t + 37 = 0
⇔[t=3717t=1
+ Với t=3717 , chọn B = 37, C = 17 ⇒A = –D = –23.
Do đó (P): –23x + 37y + 17z + 23 = 0
+ Với t = 1, chọn B = C = 1 ⇒ A = –D = 1.
Do đó (P): x + y + z – 1 = 0.
Trong không gian Oxyz, hình chiếu vuông góc của điểm A(1; 2; 5) trên trục Ox có tọa độ là
Trong không gian Oxyz, cho mặt cầu (S) có tâm I(0; 0; –3) và đi qua điểm M(4; 0; 0). Phương trình của (S) là
Trong không gian Oxyz, cho hai điểm A(3; 1; –2), B (2; –3; 5). Điểm M thuộc đoạn AB sao cho MA = 2MB, tọa độ điểm M là
Cho 21∫5dxx√x+4=aln3+bln5+cln7, với a, b, c là các số hữu tỉ. Mệnh đề nào sau đây đúng?
Cho hàm số y = f (x) liên tục trên ℝ. Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f (x), y = 0, x = –1 và x = 5 (như hình vẽ bên).
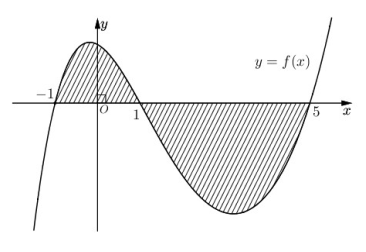
Mệnh đề nào sau đây đúng?
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(0; 1; 1) và B(1; 2; 3). Viết phương trình của mặt phẳng (P) đi qua A và vuông góc với đường thẳng AB.
Trong không gian Oxyz, cho vectơ →a=(2; −2; − 4), →b=(1; −1; 1) . Mệnh đề nào dưới đây sai?
Biết z là số phức có phần ảo âm và là nghiệm của phương trình z2 – 6z + 10 = 0. Tính tổng phần thực và ảo của số phức w=zˉz.
Cho tích phân I=1∫0x7(1+x2)5 dx, giả sử đặt t = 1 + x2. Tìm mệnh đề đúng.
Cho số phức z=(2−3i)(4−i)3+2i. Tìm tọa độ điểm biểu diễn số phức ˉz trên mặt phẳng Oxy.