Xét các số phức z thỏa mãn là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng
A. .
B. 4.
C. 2.
D. .
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
Gọi số phức
= a2 + abi – 2a – abi – b2i2 + 2bi + 2ai + 2bi2 – 4i
= (a2 + b2 – 2a – 2b) + (2a + 2b – 4)i
Để là số thuần ảo nên:
a2 + b2 – 2a – 2b = 0
a2 – 2a + 1 + b2 – 2b + 1 = 2
(a – 1)2 + (b – 1)2 = 2
Do đó tập hợp tất cả các điểm biểu diễn số phức z là một đường tròn có bán kính .
Trong không gian Oxyz, hình chiếu vuông góc của điểm A(1; 2; 5) trên trục Ox có tọa độ là
Trong không gian Oxyz, cho mặt cầu (S) có tâm I(0; 0; –3) và đi qua điểm M(4; 0; 0). Phương trình của (S) là
Trong không gian Oxyz, cho hai điểm A(3; 1; –2), B (2; –3; 5). Điểm M thuộc đoạn AB sao cho MA = 2MB, tọa độ điểm M là
Cho hàm số y = f (x) liên tục trên ℝ. Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f (x), y = 0, x = –1 và x = 5 (như hình vẽ bên).
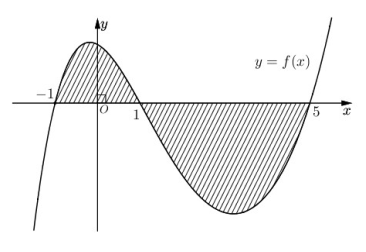
Mệnh đề nào sau đây đúng?
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(0; 1; 1) và B(1; 2; 3). Viết phương trình của mặt phẳng (P) đi qua A và vuông góc với đường thẳng AB.
Biết z là số phức có phần ảo âm và là nghiệm của phương trình z2 – 6z + 10 = 0. Tính tổng phần thực và ảo của số phức .
Cho số phức . Tìm tọa độ điểm biểu diễn số phức trên mặt phẳng Oxy.