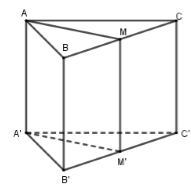
Trong không gian Oxyz, cho hình lăng trụ tam giác đều ABC.A′B′C′ có $A\text{'}(\sqrt{3};-1;1)$ hai đỉnh B,C thuộc trục Oz và AA′=1 (C không trùng với O). Biết véc tơ $\overrightarrow{u}=\left(a;b;2\right)$với $a,b\in ℝ$ là một véc tơ chỉ phương của đường thẳng A′C. Tính $T=a^2+b^2$.

Trong không gian Oxyz, cho điểm M(−1;3;2) và mặt phẳng $\left(P\right):x-2y+4z+1=0$. Đường thẳng đi qua M và vuông góc với (P) có phương trình là

Cho đường thẳng $d:\frac{x-1}{2}=\frac{y+1}{-2}=\frac{z}{3}$ và mặt phẳng (P):x+y−z−3=0. Tọa độ giao điểm của d và (P) là:

Trong không gian với hệ tọa độ Oxyz, cho d là đường thẳng đi qua điểm A(1;2;3) và vuông góc với mặt phẳng (α):4x+3y−7z+1=0. Phương trình tham số của d là:

Cho đường thẳng d có phương trình $d:\left\{\begin{array}{c}x=2t\\ y=1-t\\ z=3+t\end{array}\right.$ và mặt phẳng (P) có phương trình (P):x+y+z−10=0. Trong các khẳng định sau, khẳng định nào đúng?

Trong không gian với hệ tọa độ Oxyz cho điểm A(1;2;−3)và mặt phẳng (P):x+y−2z−1=0. Phương trình đường thẳng (d) đi qua A và vuông góc với mặt phẳng (P) là:

Cho đường thẳng d có VTCP $\overrightarrow{u}$ và mặt phẳng (P) có VTPT $\overrightarrow{n}$. Nếu d//(P) thì:

Trong không gian Oxyz cho hai mặt phẳng (P):2x+y−z−3=0  và (Q):x+y+z−1=0. Phương trình chính tắc đường thẳng giao tuyến của hai mặt phẳng (P) và (Q) là:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):x+2y−3z+4=0 và đường thẳng $d:\frac{x+2}{1}=\frac{y-2}{1}=\frac{z}{-1}$. Đường thẳng $\Delta$ nằm trong (P) đồng thời cắt và vuông góc với d có phương trình:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):x+2y=0. Phương trình nào sau đây là phương trình đường thẳng qua A(−1;3;−4) cắt trục Ox và song song với mặt phẳng (P):

Trong không gian Oxyz, gọi Δ là đường thẳng đi qua M(0;0;2) và song song với mặt phẳng $\left(P\right):x+y+z+3=0$sao cho khoảng cách từ A(5;0;0) đến đường thẳng $\Delta$ nhỏ nhất. Một vectơ chỉ phương của đường thẳng $\Delta$ là

Trong không gian Oxyz, cho mặt phẳng (P):4y−z+3=0 và hai đường thẳng ${\Delta }_1:\frac{x-1}{1}=\frac{y+2}{4}=\frac{z-2}{3}, {\Delta }_2:\frac{x+4}{5}=\frac{y+7}{9}=\frac{z}{1}$. Đường thẳng d vuông góc với mặt phẳng (P) và cắt cả hai đường thẳng ${\Delta }_1,{\Delta }_{2 }$ có phương trình là

Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và 2 đường thẳng$d_1:\frac{x+3}{1}=\frac{y-6}{-1}=\frac{z}{-1};d_2:\left\{\begin{array}{c}x=1+2t\\ y=5-3t\\ z=4\end{array}\right.$. Phương trình mặt phẳng qua A và song song với $d_1,d_2$ là:

Cho $d:\frac{x+1}{2}=\frac{y-3}{m}=\frac{z-1}{m-2};\left(P\right):x+3y+2z-5=0$. Tìm m để d và (P) vuông góc với nhau.