Cho tam giác ABC nhọn có ba đường cao AM, BN, CP. Biết AM = BN = CP. Khi đó tam giác ABC là:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
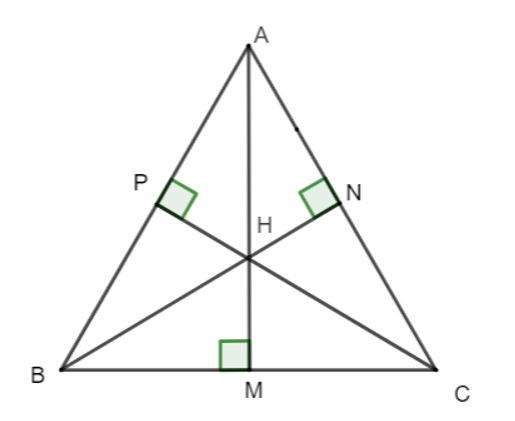
Gọi H là giao điểm của ba đường cao.
Ta có: + = 90°;
+ = 90°;
= (hai góc đối đỉnh).
Do đó = .
Xét ∆ABM vuông tại M và ∆CBP vuông tại P ta có:
= (cmt).
AM = CP (gt).
Do đó ∆ABM = ∆CBP (cạnh góc vuông - góc nhọn).
Suy ra AB = BC (hai cạnh tương ứng) (1)
Chứng minh tương tự ta được ∆BNC = ∆AMC (cạnh góc vuông - góc nhọn)
Suy ra BC = AC (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra AB = BC = AC.
Vậy ∆ABC là tam giác đều.
Điền vào chỗ trống sau: “Ba đường cao của một tam giác cùng đi qua một điểm. Điểm này được gọi là … của tam giác”.
Điền vào chỗ trống sau: “Đoạn thẳng vuông góc kẻ từ một đỉnh của một tam giác đến đường thẳng chứa cạnh đối diện gọi là … của tam giác đó”.
Cho ΔABC vuông cân tại B. Trên cạnh AB lấy điểm H. Trên tia đối của tia BC lấy điểm D sao cho BH = BD. Chọn câu đúng.
Cho tam giác ABC vuông tại A. Lấy điểm O thuộc AB. Vẽ OM vuông góc với BC tại M. Tia MO cắt AC tại N. Chọn câu đúng.
Cho tam giác ABC có đường cao BE và trực tâm O .AO cắt BC tại H. Số đo là:
Cho tam giác ABC có đường cao AH và BE cắt nhau tại O. Cho = 50°. Số đo góc bằng :
Cho ΔABC, hai đường cao AM và BN cắt nhau tại H. Em chọn phát biểu đúng.
Cho tam giác ABC có đường cao AH và BE cắt nhau tại O. Cho = 30°. Số đo bằng :
