Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O và có SA = SC, SB = SD. Trong các khẳng định sau, khẳng định nào đúng?
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
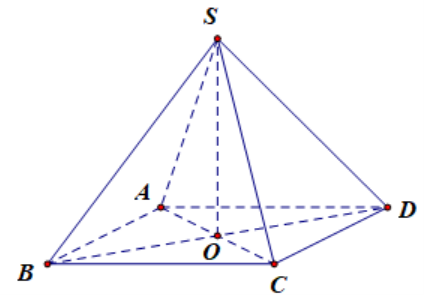
Ta có
∙ SA = SC Þ Tam giác SAC cân tại S
Þ SO là đường cao tam giác SAC Þ SO ^ AC (1)
∙ SB = SD Þ Tam giác SBD cân tại S
Þ SO là đường cao tam giác SBD Þ SO ^ BD (2)
Từ (1) và (2) suy ra SO ^ (ABCD).
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC) và SA = a. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng:
Đường thẳng y = ax + b tiếp xúc với đồ thị hàm số y = x3 – 3x – 1 tại điểm có hoành độ bằng 2, giá trị của a + b bằng:
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - 5x + 1}}{{1 + 3x - {x^2}}}\) bằng:
\(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {4{x^2} - 4x + 7} - 2x} \right)\) bằng:
Phương trình tiếp tuyến của đồ thị hàm số y = x4 – 3x2 + 1 tại điểm M(1;−1) là:
\(\mathop {\lim }\limits_{x \to 2} \left( { - 3{x^2} + 6x + 1} \right)\) bằng:
