Cho nửa đường tròn (O) đường kính AB = 2R. Điểm C (khác A) bất kì nằm trên nửa đường tròn sao cho AC < CB. Điểm D thuộc cung nhỏ BC sao cho COD = 90o. Gọi E là giao điểm của AD và BC, F là giao điểm của AC và BD.
a) Chứng minh CEDF là tứ giác nội tiếp.
Giải bởi Vietjack
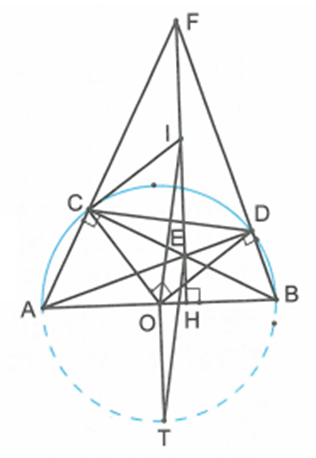
Ta có ACB = ADB = 90o (góc nội tiếp chắn nửa đường tròn)
=> FCE = FDE = 90o.
Tứ giác CEDF có FCE + FDE = 180o => CEDF là tứ giác nội tiếp.
Cho tam giác ABC và đường cao AH. Gọi M, N lần lượt là trung điểm của AB, AC. Đường tròn ngoại tiếp tam giác BHM cắt đường tròn ngoại tiếp tam giác CNH tại E. Chứng minh AMEN là tứ giác nội tiếp và HE đi qua trung điểm của MN.
c) Gọi I là trung điểm của EF. Chứng minh IC là tiếp tuyến của (O).
Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I ( I nằm giữa A và O). Lấy điểm E trên cung nhỏ BC ( E khác B và C ), AE cắt CD tại F. Chứng minh BEFI là tứ giác nội tiếp đường tròn.
