Trên các cạnh BC, BD của hình vuông ABCD ta lấy lần lượt các điểm M, N sao cho MAN = 45. Đường thẳng BD cắt các đường thẳng AM, AN tương ứng tại các điểm P, Q.
a) Chứng minh rằng các tứ giác ABMQ và ADNP nội tiếp.
 Giải bởi Vietjack
Giải bởi Vietjack
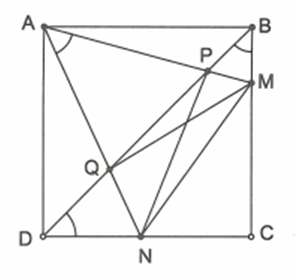
Các đỉnh A và B cùng nhìn đoạn thẳng MQ dưới một góc 45.
Vì vậy tứ giác ABMQ nội tiếp.
Tương tự ta suy ra tứ giác ADNP nội tiếp.
c) Gọi N là giao điểm của tia AM và tia DC; K là giao điểm của BN và tia EM. Chứng minh BKCE là tứ giác nội tiếp.
Cho hình vuông ABCD có hai đường chéo cắt nhau tại E. Lấy I thuộc cạnh AB, M thuộc cạnh BC sao cho IEM = 90 (I và M không trùng với các đỉnh của hình vuông).
a) Chứng minh rằng BIEM là tứ giác nội tiếp.
b) Chứng minh rằng các điểm M, N, P, Q, C nằm trên cùng một đường tròn.
Cho đường tròn ( O ; R) và dây BC cố định, A là điểm di động trên cung lớn BC (A khác B, C) sao cho tam giác ABC nhọn. Các đường cao BD và CE của tam giác ABC cắt nhau tại điểm H. Kẻ đường kính AF của đường tròn ( O ), AF cắt BC tại điểm N.
a) Chứng minh tứ giác BEDC là tứ giác nội tiếp.
c) Tìm hệ thức liên hệ giữa sđ AC và sđ AD để AK song song với ND.
Cho đường tròn đường kính AB, các điểm C , D nằm trên đường tròn đó sao cho C , D nằm khác phía đối với đường thẳng AB, đồng thời AD > AC. Gọi điểm chính giữa của các cung nhỏ AC, AD lần lượt là M , N; giao điểm của MD với CN là K; giao điểm của MN và AC, AD lần lượt là H , I.
a) Chứng minh ACN = DMN. Từ đó suy ra tứ giác MCKH.