Cho tam giác ABC (AB<AC) có ba góc nhọn nội tiếp đường tròn (O) và D là hình chiếu vuông góc của B trên AO sao cho D nằm giữa A và D. Gọi M là trung điểm của BC, N là giao điểm của BD và AC, F là giao điểm của MD và AC, E là giao điểm thứ hai của BD với đường tròn (O). H là giao điểm của BF và AD. Chứng minh rằng:
a) Tứ giác BDOM nội tiếp và . Giải bởi Vietjack
Giải bởi Vietjack
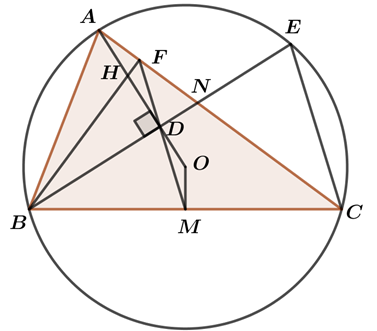
a)
M là trung điểm BD suy ra
Tứ giác BDOM có
suy ra tứ giác BDOM nội tiếp.
Vì tứ giác BDOM nội tiếp
suy ra
Mà (góc nội tiếp cùng chắn cung ).
Cho điểm M nằm bên ngoài đường tròn (O; R). Từ điểm M kẻ hai tiếp tuyến MA,MB với đường tròn đó ( A, B là các tiếp điểm ). Qua điểm A kẻ đường thẳng song song với MB cắt đường tròn (O;R) tại C. Nối MC cắt đường tròn (O; R) tại D. Tia AD cắt MB tại E .
a) Chứng minh MAOB là tứ giác nội tiếp.
Cho nửa đường tròn tâm O đường kính AB=2R. Gọi M là điểm chính giữa của cung AB, N là điểm bất kỳ thuộc cung MB (N khác M và B). Tia AM và AN cắt tiếp tuyến tại B của nửa đường tròn tâm O lần lượt tại C và D
1. Tính số đo .
Cho đường tròn (O) của đường kính AB. Vẽ tiếp tuyến Ax với đường tròn(O) ( A là tiếp điểm). Qua C thuộc tia Ax vẽ đường thẳng cắt đường tròn (O) tại hai điểm D và E ( D nằm giữa C và E; D và E nằm về hai phía của đường thẳng AB). Từ O vẽ OH vuông góc với đoạn thẳng DE tại H.
a) Tứ giác AOHC nội tiếp.
2. Từ điểm A nằm ngoài đường tròn (O). Vẽ hai tiếp tuyến AB, AC với đường tròn (O), (B, C là hai tiếp điểm).
a) Chứng minh tứ giác ABOC nội tiếp được đường tròn.
Cho đường tròn (O), từ một điểm M nằm ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB của đường tròn (A, B là hai tiếp điểm). Kẻ đường kính BE của đường tròn (O). Gọi F là giao điểm thứ hai của đường thẳng ME và đường tròn (O). Đường thẳng AF cắt MO tại điểm N. Gọi H là giao điểm của MO và AB.
1. Chứng minh tứ giác MAOB nội tiếp đường tròn.
Cho tứ giác ABCD nội tiếp đường tròn tâm O, đường kính AD=2R..Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc với AD tại F
1. Chứng minh ABEF nội tiếp.
Cho đường tròn tâm O, đường kính AB. Trên tiếp tuyến của đường tròn (O) tại A lấy điểm M(M khác A ). Từ M vẽ tiếp tuyến thứ hai MC với đường tròn (O) (C là tiếp điểm). Kẻ (),MB cắt đường tròn (O) tại điểm thứ hai là K và cắt CH tại N. Chứng minh rằng:
a) Tứ giác AKNH nội tiếp trong một đường tròn.
Cho nhọn (AB<AC) nội tiếp đường tròn (O). Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau tại D. OD cắt BC tại E. Qua D vẽ đường thẳng song song với AB, đường thẳng này cắt AC tại K. đường thẳng OK cắt AB tại F. Tính tỉ số diện tích
Cho tứ giác ABCD nội tiếp đường tròn đường kính AB. Hai đường chéo AC và BD cắt nhau tại E, F là hình chiếu vuông góc của E trên AB.
1. Chứng minh tứ giác ADEF nội tiếp.
Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn (C) tâm O bán kính R. Hai đường cao AE và BK tam giác ABC cắt nhau tại H (với E thuộc BC, K thuộc AC).
1. Chứng minh rằng tứ giác ABEK nội tiếp được trong một đường tròn.