Cho tứ diện ABCD. M, N là hai điểm lần lượt thuộc hai cạnh AB, AC sao cho MN cắt BC tại I. Khẳng định nào sau đây là đúng
 Giải bởi Vietjack
Giải bởi Vietjack
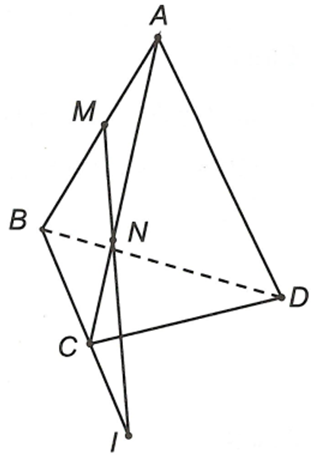
Ta có:
D là điểm chung của (DMN), (DBC)
I là điểm chung của (DMN), (DBC)
Vậy
Cho bốn điểm A, B, C, D không đồng phẳng. Trên hai đoạn thẳng AB, AC lần lượt lấy các điểm M, N sao cho và . Tìm giao tuyến của (DMN) và (BCD).
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD. Tìm giao tuyến của mặt phẳng (ACD) và (GAB).
Cho hình chóp S.ABCD, gọi O là giao điểm của AC và BD. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng
Cho tứ diện ABCD, gọi M, N lần lượt là trung điểm của CD và AD, G là trọng tâm tam giác ACD. BG là giao tuyến của hai mặt phẳng nào?
Cho hình chóp S.ABCD. Giao tuyến của hai mặt phẳng (SAB) và (SBC) là đường thẳng
Trong mặt phẳng cho tức giác ABCD có các cặp cạnh đối không song song và . Xác định giao tuyến của các cặp mặt phẳng sau đây:
a) và
Cho S là một điểm không thuộc mặt phẳng chứa hình bình hành ABCD. Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
Cho tứ diện ABCD, gọi N và K lần lượt là trung điềm của AD và BC. NK là giao tuyến của mặt phẳng (BCA/) với mặt phẳng nào
Cho hình chóp S.ABCD với AC và BD giao nhau tại M, AB và CD giao nhau tại N. Hai mặt phẳng (SAB) và (SCD) có giao tuyến là
Cho hình chóp S.ABCD, gọi O là giao điểm của AC và BD. Giao tuyến của hai mặt phẳng (SAD) và (SBD) là đường thẳng
Cho hình chóp S.ABC, gọi G là trọng tâm của tam giác ABC; M, N lần lượt là trung điềm BC, AC. Giao tuyến của (SAM) và (SBN) là
Cho tứ diện ABCD. Gọi I, J và K lần lượt là trung điểm của AC, BC và BD. Giao tuyến của hai mặt phẳng (ABD) và (IJK) là
Cho tứ diện ABCD có I, J lần lượt là trung điểm AC, BC. Gọi K thuộc BD sao cho KD < KB. Gọi E là giao điểm của JK và CD, F là giao điểm của AD và IE. Giao tuyến của (IJK) và (ACD) là
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AD là đáy lớn). Gọi O là giao điểm của AC và BD, I là giao điểm của AB và CD. Giao tuyến của (SAB) và (SCO) là