Trên đường chéo AC của hình bình hành ABCD lấy một điểm I. Qua I kẻ hai đường thẳng bất kì sao cho đường thứ nhất cắt AB,CD lần lượt ở E và F, đường thẳng thứ hai cắt AD,BC theo thứ tự ở G và H. Chứng minh rằng GE//FH.
Giải bởi Vietjack
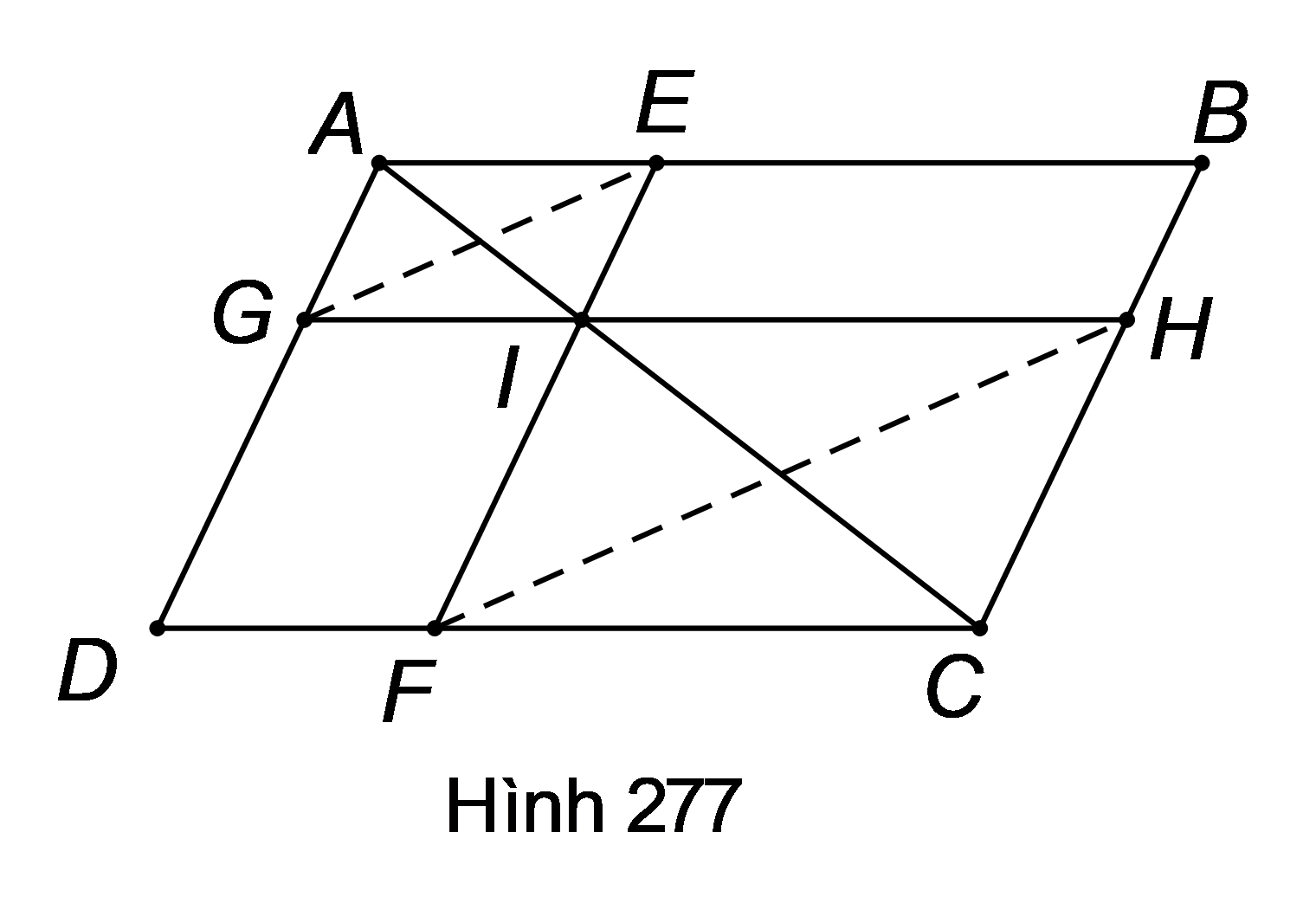
ABCD là hình bình hành nên và , suy ra .
Áp dụng hệ quả của định lí Ta-lét cho và , ta được:
.
Điều này chứng tỏ đường thẳng EG cắt hai cạnh của tam giác IHF và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ, nên (theo định lí Ta-lét đảo).
Cho tứ giác ABCD. Đường thẳng qua A và song song với BC cắt BD ở E. Đường thẳng qua B và song song với AD cắt AC ở G. Chứng minh rằng EG//CD.
