Tam giác ABC có đường cao AH. Đường thẳng d song song với BC cắt các cạnh AB, AC và đường cao AH lần lượt tại B’, C’ và H’.
Chứng minh rằng
 Giải bởi Vietjack
Giải bởi Vietjack
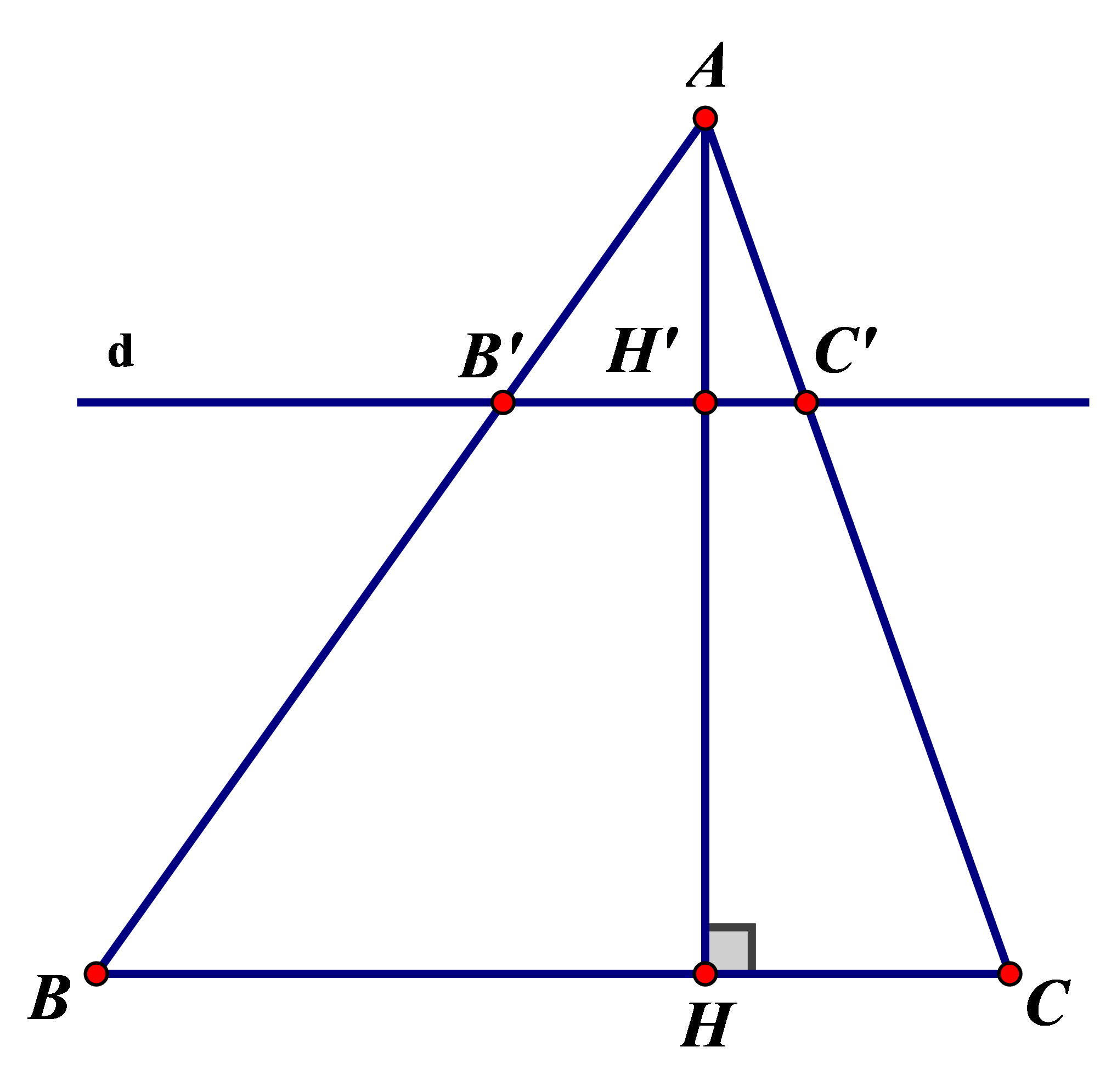
Trong suy ra (hệ quả của định lí Ta-let) (1)
Trong suy ra ( hệ quả của định lí Ta-let) (2)
Trong suy ra ( hệ quả của định lí Ta-let) (3)
Từ (1), (2) và (3) suy ra:
Cho tam giác ABC, điểm I nằm trong tam giác, các tia AI, BI, CI cắt các cạnh BC, AC, AB theo thứ tự ở D, E, F. Qua A kẻ đường thẳng song song với BC cắt tia CI tại H và cắt tia BI tại K. Chứng minh:
Cho biết và diện tích tam giác ABC là 67,5cm2. Hãy tính diện tích tam giác .
Cho tam giác ABC, điểm I thuộc cạnh AB, điểm K thuộc cạnh AC. Kẻ IM song song với BK (M thuộc AC), kẻ KN song song với CI (N thuộc AB).Chứng minh MN song song với BC.
Cho tứ giác ABCD. Qua kẻ đường thẳng song song với DC cắt AC ở G. Qua G kẻ đường thẳng song song với CB cắt AB tại H.
Qua B kẻ đường thẳng song song với CD, cắt đường thẳng Ac tại I. Qua C kẻ đường thẳng song song với BA, cắt BD tại F. Chứng minh IF//AD .
ADMI là hình hình hành
Cho tứ giác ABCD. Qua kẻ đường thẳng song song với DC cắt AC ở G. Qua G kẻ đường thẳng song song với CB cắt AB tại H. Chứng minh rằng: HE//BD
Cho hình thang ABCD (AB//CD), M là trung điểm của CD. Gọi I là giao điểm của AM và BD, K là giao điểm của BM và AC.
Chứng minh
Cho tam giác ABC, điểm I nằm trong tam giác, các tia AI, BI, CI cắt các cạnh BC, AC, AB theo thứ tự ở D, E, F. Qua A kẻ đường thẳng song song với BC cắt tia CI tại H và cắt tia BI tại K. Chứng minh: