14 câu hỏi trắc nghiệm thuộc Dạng 5. Bài luyện tập dạng cơ bản có đáp án

Câu 1:

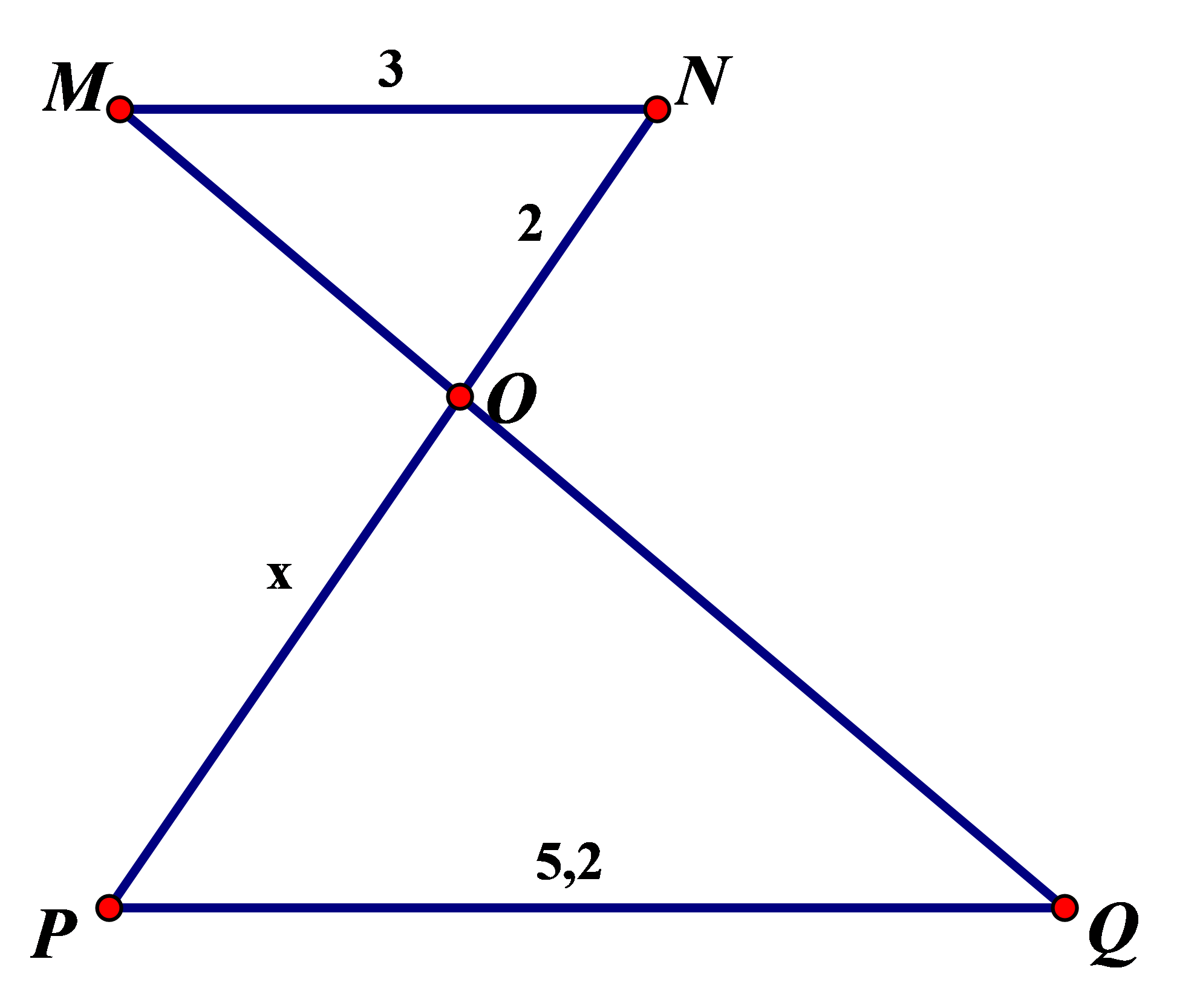
Hình 1. Trong tam giác ABC, $Δ O P Q, M N / / P Q$ ta có: $\frac{O P}{O N} = \frac{P Q}{M N}$ ( hệ quả của định lí Ta-let)

$\Leftrightarrow \frac{x}{2} = \frac{5, 2}{3} \Leftrightarrow x = \frac{5, 2.2}{3} = \frac{52}{15} (c m)$

Câu 2:

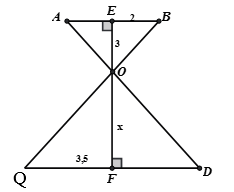
Tìm x trong hình 2

Media VietJack

Xem đáp án

Hình 2. Ta có: $E F ⊥ A B; E F ⊥ Q D$ Suy ra $A B / / Q D$ .

Trong $Δ O Q F, Q F / / E B$ suy ra: $\frac{O F}{O E} = \frac{F Q}{E B}$ ( hệ quả của định lí Ta-let)

$\Leftrightarrow \frac{x}{3} = \frac{3, 5}{2} \Leftrightarrow x = \frac{3.3, 5}{2} = 5, 25 (c m)$

Câu 3:

Tìm x trong hình 3

Xem đáp án

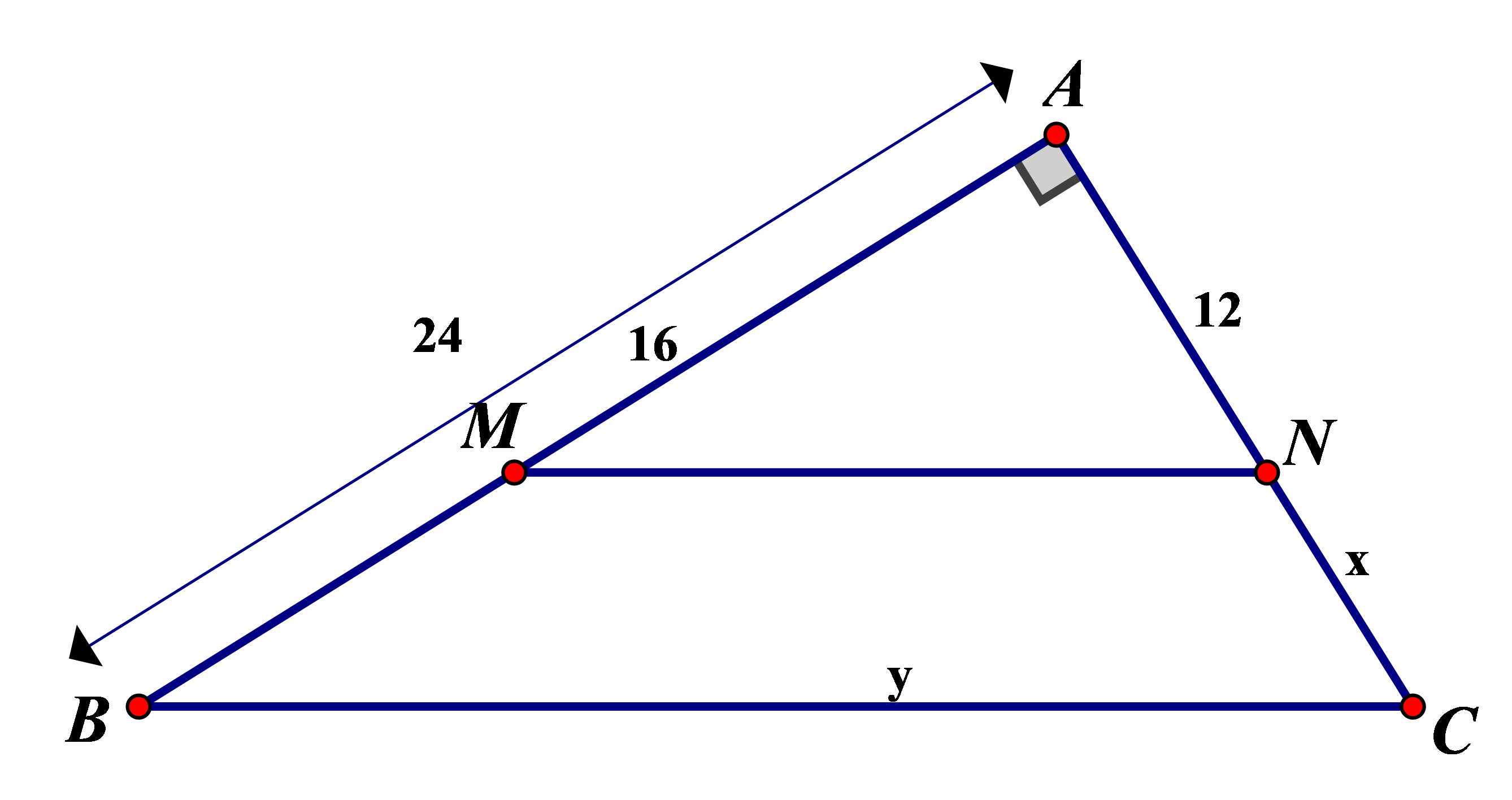
Hình 3.Áp dụng định lí Pytago trong $Δ A M N, \hat{A} = 90^{0}$ ta có:

$M N^{2} = A M^{2} + A N^{2} = 16^{2} + 12^{2} \Rightarrow M N = \sqrt{400} = 20 (c m)$

Trong $Δ A M N, M N / / B C$ suy ra: $\frac{A M}{A B} = \frac{A N}{A C}$ ( hệ quả của định lí Ta-let)

$\Leftrightarrow \frac{16}{24} = \frac{12}{A C} \Leftrightarrow A C = \frac{24.12}{16} = 18 (c m)$ ;

Trong $Δ A M N, M N / / B C$ suy ra: $\frac{A M}{A B} = \frac{M N}{B C}$ ( hệ quả của định lí Ta-let)

$\Leftrightarrow \frac{16}{24} = \frac{20}{B C} \Leftrightarrow B C = \frac{24.20}{16} = 30 (c m)$

Câu 4:

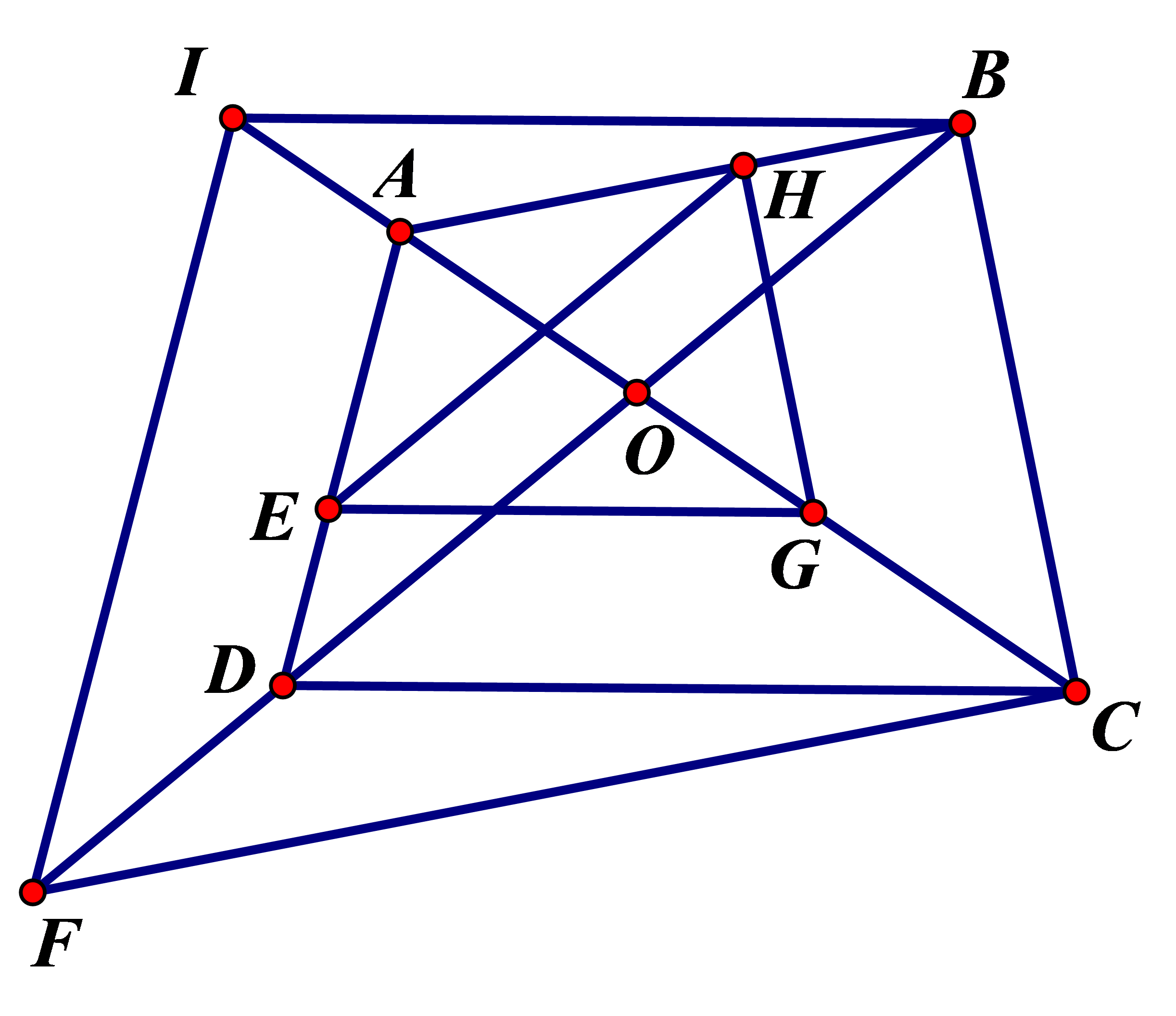
Cho tam giác ABC, điểm I nằm trong tam giác, các tia AI, BI, CI cắt các cạnh BC, AC, AB theo thứ tự ở D, E, F. Qua A kẻ đường thẳng song song với BC cắt tia CI tại H và cắt tia BI tại K. Chứng minh: $\frac{A K}{B D} = \frac{H A}{D C}$

Xem đáp án

$A K / / B D \Rightarrow \frac{A I}{I D} = \frac{A K}{B D}$

Từ $A H / / D C \Rightarrow \frac{A I}{I D} = \frac{A H}{D C}$

Do đó $\frac{A K}{B D} = \frac{A H}{D C}$

Câu 5:

Cho tam giác ABC, điểm I nằm trong tam giác, các tia AI, BI, CI cắt các cạnh BC, AC, AB theo thứ tự ở D, E, F. Qua A kẻ đường thẳng song song với BC cắt tia CI tại H và cắt tia BI tại K. Chứng minh: $\frac{A F}{B F} + \frac{A E}{C E} = \frac{A I}{I D} .$

Xem đáp án

Ta có: $\frac{A K}{B D} = \frac{A H}{D C} = \frac{A K + A H}{B D + D C} = \frac{H K}{B C} = \frac{A I}{I D}$

Ta chứng minh

$\frac{A F}{B F} = \frac{A H}{B C} (2); \frac{A E}{C E} = \frac{A K}{B C} (3)$

Từ (1), (2), (3) ta có $\frac{A E}{C E} + \frac{A F}{B F} = \frac{A I}{I D}$ (đpcm)

Câu 6:

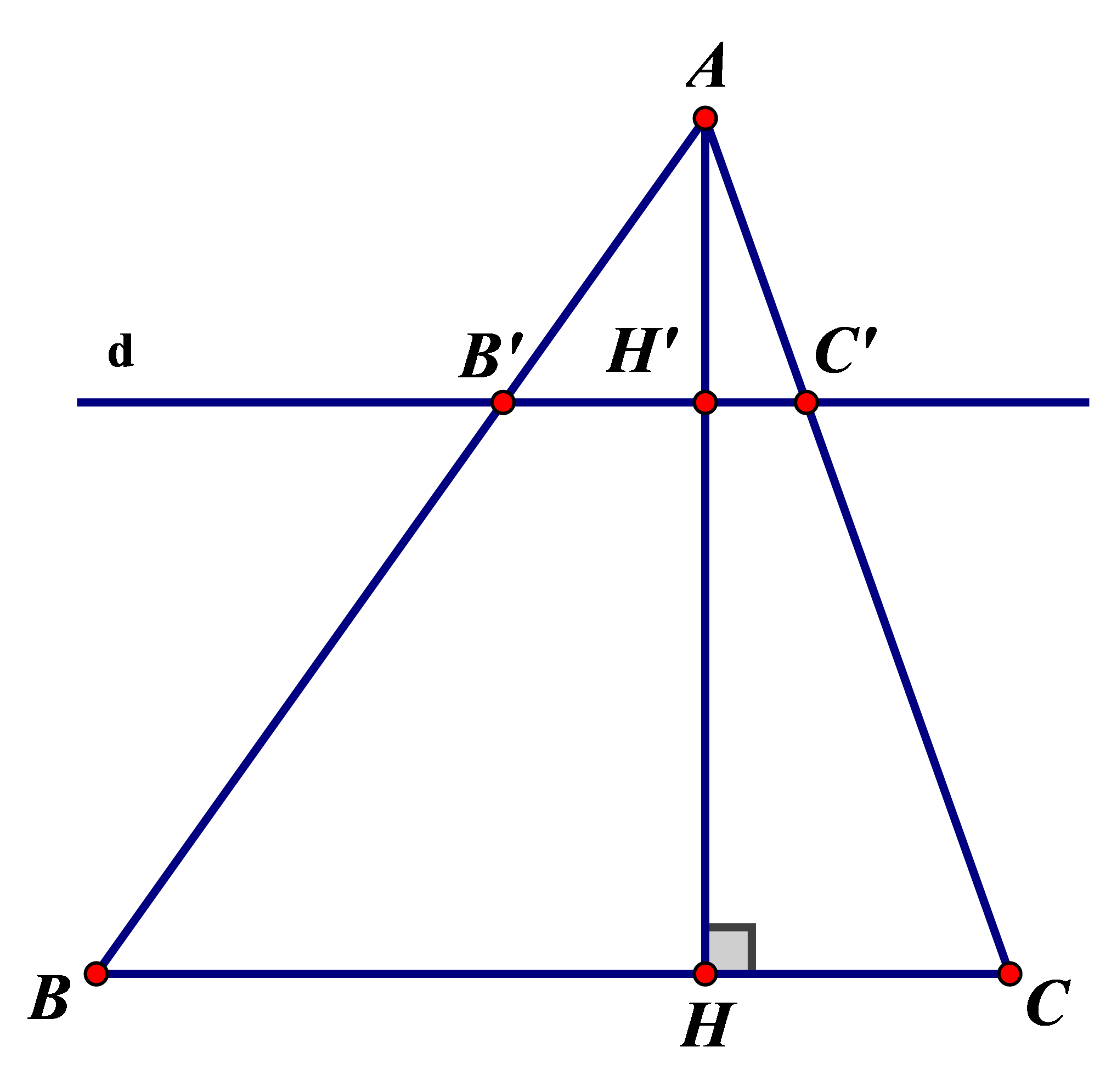
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC cắt các cạnh AB, AC và đường cao AH lần lượt tại B’, C’ và H’.

Chứng minh rằng $\frac{A H'}{A H} = \frac{B' C'}{B C}$

Xem đáp án

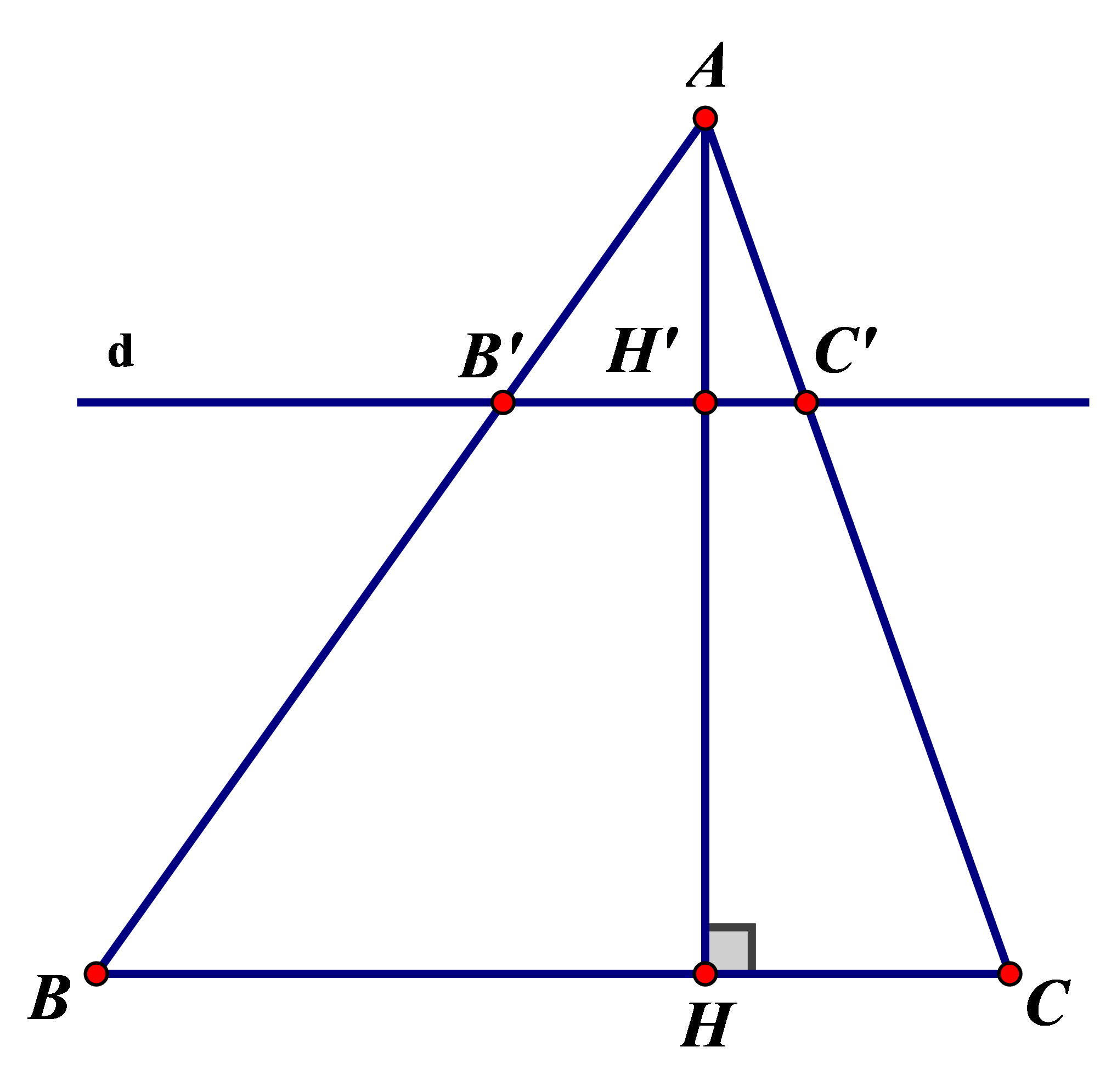
Trong $Δ A B H, B' H' / / B H$ suy ra $\frac{A H'}{A H} = \frac{A B'}{A B}$ (hệ quả của định lí Ta-let) (1)

Trong $Δ A C H, C' H' / / C H$ suy ra $\frac{A H'}{A H} = \frac{A C'}{A C}$ ( hệ quả của định lí Ta-let) (2)

Trong $Δ A B C, B' C' / / B C$ suy ra $\frac{A B'}{A B} = \frac{A C'}{A C}$ ( hệ quả của định lí Ta-let) (3)

Từ (1), (2) và (3) suy ra: $\frac{A H'}{A H} = \frac{B' C'}{B C}$

Câu 7:

Tam giác ABC có đường cao AH. Đường thẳng d song song với BC cắt các cạnh AB, AC và đường cao AH lần lượt tại B’, C’ và H’.

Cho biết $A H' = \frac{A H}{3}$ và diện tích tam giác ABC là 67,5cm². Hãy tính diện tích tam giác $A B' C'$ .

Xem đáp án

Ta có: $\frac{A H'}{A H} = \frac{B' C'}{B C}$ ( câu a); $\frac{B' C'}{B C} = \frac{1}{3} \Rightarrow B' C' = \frac{1}{3} B C$

Từ đó suy ra:

\frac{S_{A B' C'}}{S_{A B C}} = \frac{\frac{1}{2} A H' . B' C'}{\frac{1}{2} A H . B C} = \frac{A H'}{A H} . \frac{B' C'}{B C} = \frac{1}{9} \Rightarrow S_{A B' C'} = \frac{1}{9} S_{A B C} = \frac{67, 5}{9} = 9, 5 (c m^{2})

Câu 8:

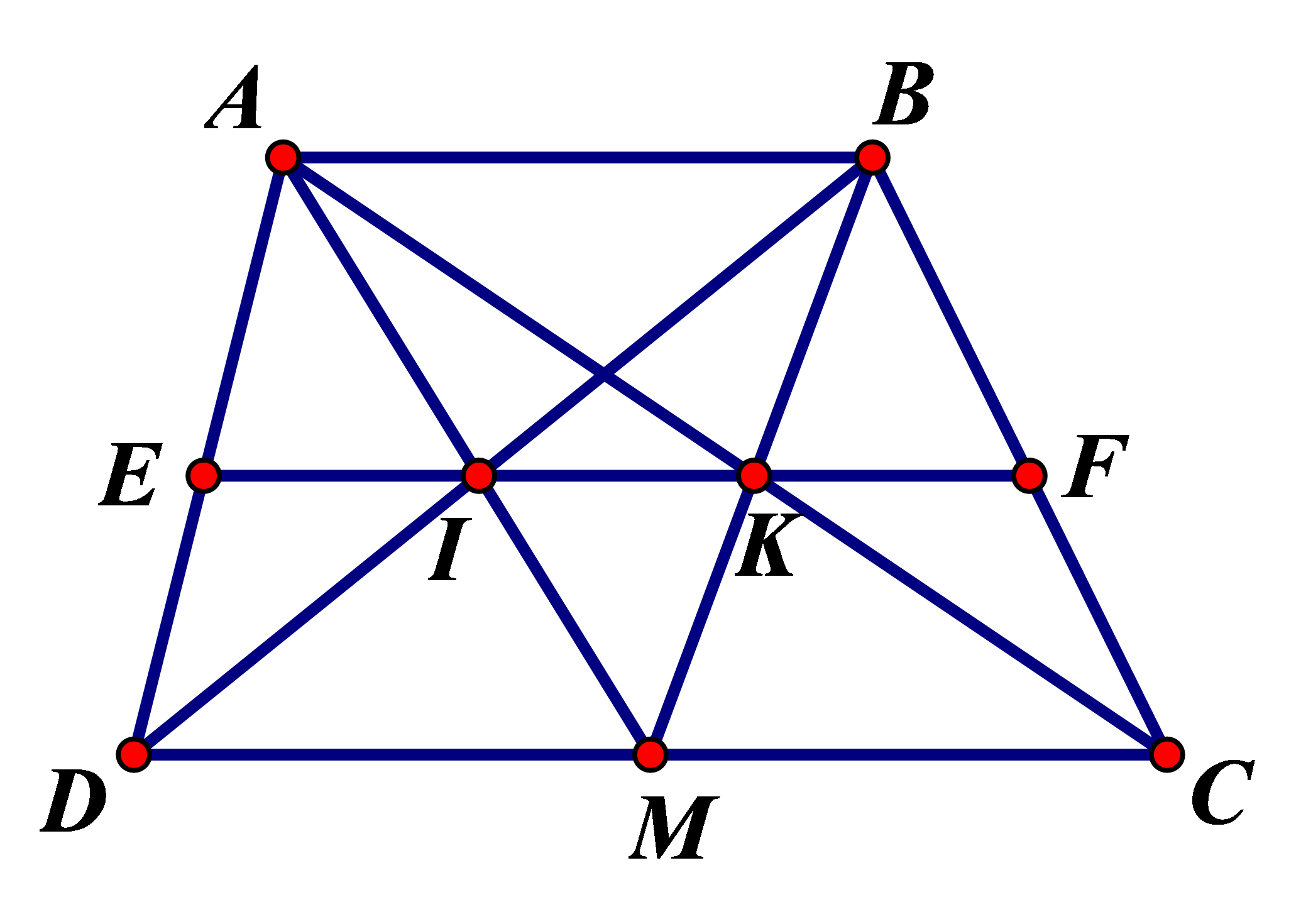
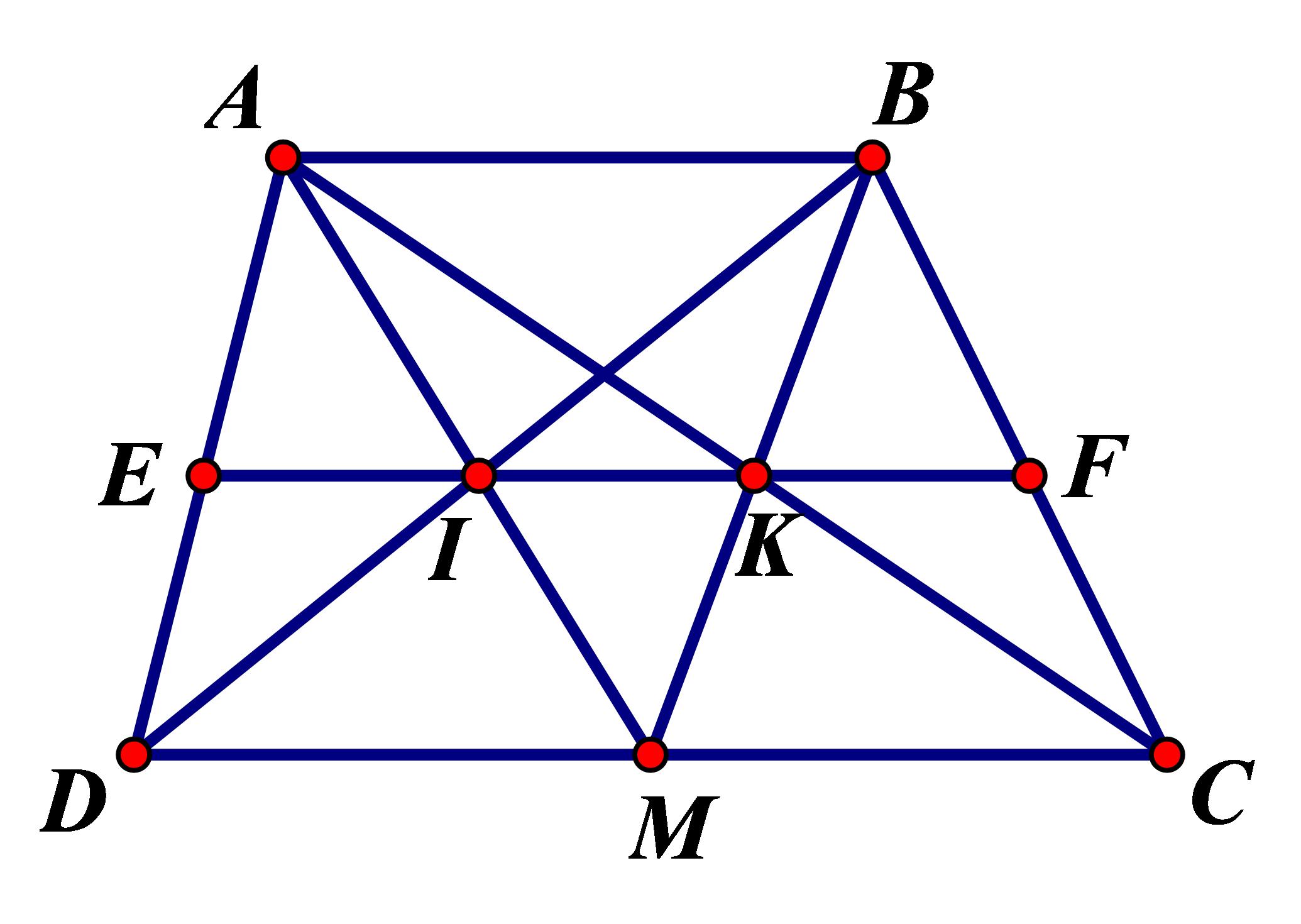
Cho tam giác ABC, điểm I thuộc cạnh AB, điểm K thuộc cạnh AC. Kẻ IM song song với BK (M thuộc AC), kẻ KN song song với CI (N thuộc AB).Chứng minh MN song song với BC.

Xem đáp án

Từ $I M // B K$ và $K N // I C$ ta suy ra $\frac{A I}{A B} = \frac{A M}{A K}$ và $\frac{A N}{A I} = \frac{A K}{A C}$ .

Do đó $\frac{A N}{A B} = \frac{A M}{A C}$ Þ $M N //BC$ .

Câu 9:

(Định lý Céva) Trên ba cạnh BC, CA, AB của tam giác ABC lấy tương ứng ba điểm P, Q, R. Chứng minh nếu AP, BQ, CR đồng quy thì

\frac{P B}{P C} . \frac{Q C}{Q A} . \frac{R A}{R B} = 1.

Xem đáp án

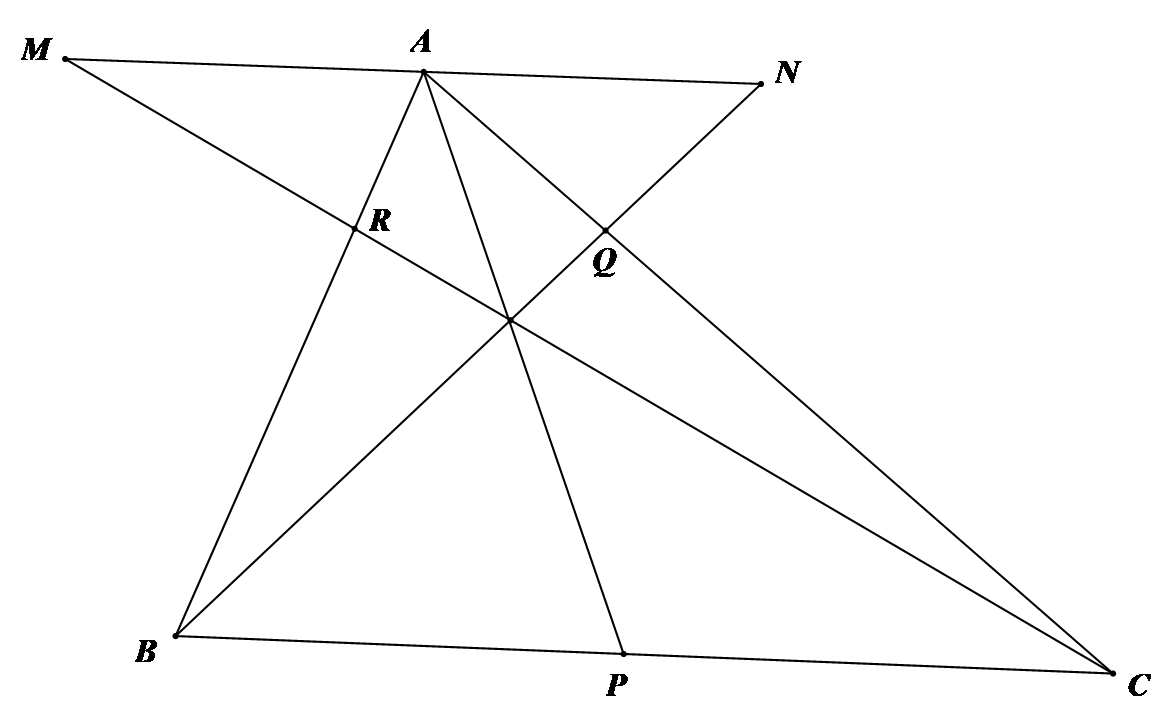
Qua A kẻ đường thẳng song song với BC cắt BQ và CR lần lượt tại N và M.

Ta chứng minh được: $\frac{Q C}{A Q} = \frac{B C}{A N}$ (1)

$\frac{R A}{B R} = \frac{A M}{B C} (2)$ ; $\frac{B P}{C P} = \frac{A N}{A M}$ (3)

Từ (1), (2), (3) suy ra $\frac{P B}{P C} \cdot \frac{Q C}{Q A} \cdot \frac{R A}{R B} = 1$ (đpcm)

Câu 10:

Cho tứ giác ABCD. Qua kẻ đường thẳng song song với DC cắt AC ở G. Qua G kẻ đường thẳng song song với CB cắt AB tại H. Chứng minh rằng: HE//BD

Xem đáp án

$\begin{array}{l} E G / / D C \Rightarrow \frac{A E}{A D} = \frac{A G}{A C} \\ G H / / B C \Rightarrow \frac{A G}{A C} = \frac{A H}{A B} \end{array}\} \Rightarrow \frac{A E}{A D} = \frac{A H}{A B} \Rightarrow E H / / B D$

Câu 11:

Cho tứ giác ABCD. Qua kẻ đường thẳng song song với DC cắt AC ở G. Qua G kẻ đường thẳng song song với CB cắt AB tại H.

Qua B kẻ đường thẳng song song với CD, cắt đường thẳng Ac tại I. Qua C kẻ đường thẳng song song với BA, cắt BD tại F. Chứng minh IF//AD .

Xem đáp án

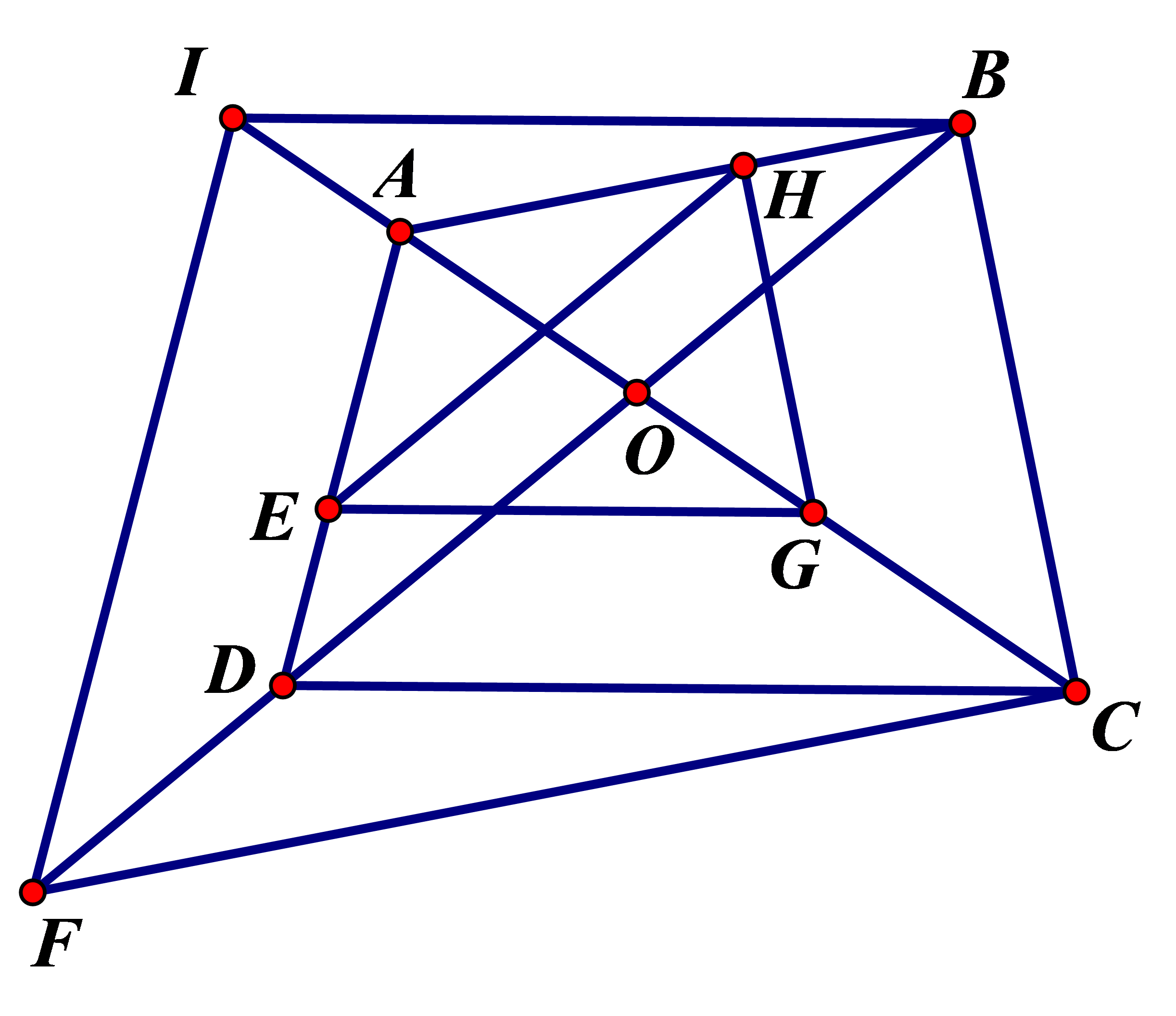
Gọi O là giao điểm của AC và BD

$\begin{array}{l} B I / / D C \Rightarrow \frac{O I}{O C} = \frac{O B}{O D} \\ A B / / C F \Rightarrow \frac{O C}{O A} = \frac{O F}{O B} \end{array}\} \Rightarrow \frac{O I}{O A} = \frac{O F}{O D} \Rightarrow A D / IF$

Câu 12:

Cho hình thang ABCD (AB//CD), M là trung điểm của CD. Gọi I là giao điểm của AM và BD, K là giao điểm của BM và AC.

Chứng minh $I K // A B$

Xem đáp án

$\begin{array}{l} A B / / D M \Rightarrow \frac{I M}{I A} = \frac{M D}{A B} \\ A B / / M C \Rightarrow \frac{M K}{K B} = \frac{M C}{A B} \end{array}\} \Rightarrow \frac{I M}{I A} = \frac{M K}{K B} \Rightarrow I K / / A B$

Câu 13:

Cho hình thang ABCD (AB//CD), M là trung điểm của CD. Gọi I là giao điểm của AM và BD, K là giao điểm của BM và AC.

Đường thẳng IK cắt AD, BC theo thứ tự ở E và F. Chứng minh rằng

E I = I K = K F .

Xem đáp án

Ta có:

$\begin{array}{l} A B / / E I \Rightarrow \frac{I E}{A B} = \frac{I D}{D B} \\ A B / / I K \Rightarrow \frac{I K}{A B} = \frac{I M}{M A} \\ A B / / D M \Rightarrow \frac{D I}{B I} = \frac{I M}{I A} \Rightarrow \frac{D I}{B D} = \frac{I M}{A M} \end{array}\} \Rightarrow \frac{I E}{A B} = \frac{I K}{A B} \Rightarrow E I = I K$

Tương tự $I K = K F$ . Do đó $E I = I K = K F$ .

Câu 14:

Cho

Δ A B C

có AD là trung tuyến. Từ một điểm M bất kỳ trên cạnh BC, vẽ đường thẳng song song với AD, cắt AB và AC lần lượt tại E và F. Gọi I là trung điểm của EF. Chứng minh :

ADMI là hình hình hành

Xem đáp án

$M E + M F = 2 A D$ (cmt)

Mà $M E + M F = F E + M F + M F = F E + 2 M F = 2 I F + 2 M F = 2 I M$

$\begin{array}{l} \Rightarrow A D = I M \\ A D / / I M \end{array}\} \Rightarrow A D I M$ là hình bình hành