Trắc nghiệm chuyên đề Toán 8 Chủ đề 10. Ôn tập và kiểm tra có đáp án
-
1587 lượt thi
-
66 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Điều kiện xác định của phân thức 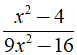
 Xem đáp án
Xem đáp án
Chọn đáp án A.
Ta có điều kiện xác định của phân thức 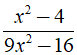 là 9x2 - 16 ≠ 0
là 9x2 - 16 ≠ 0
⇔ 9x2 ≠ 16 ⇔ x2 ≠ ⇔ x ≠ ± .
Câu 4:
 Xem đáp án
Xem đáp án
Chọn đáp án D.
Nhớ lại định nghĩa: Một phân thức đại số (hay nói gọn là phân thức) là một biểu thức có dạng A/B, trong đó A, B là những đa thức và B khác đa thức 0.
+ có A = 1;B = x2 + 1 ≠ 0 ⇒ là phân thức đại số.
+ có A = x + 1;B = 2 ≠ 0 ⇒ là phân thức đại số.
+ x2 - 5 có A = x2 - 5;B = 1 ⇒ x2 - 5 là phân thức đại số.
+ có A = x + 1;B = 0 ⇒ (x + 1)/0 không phải là phân thức đại số .
Câu 5:
 Xem đáp án
Xem đáp án
Chọn đáp án C.
Nhân cả tử và mẫu với đa thức ( x + 1 ) ta được phân thức mới là
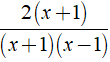
Ta có
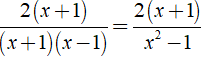
(áp dụng hằng đẳng thức A2 - B2 = ( A - B )( A + B ) )
Câu 6:
 Xem đáp án
Xem đáp án
Chọn đáp án C.
+ Giá trị của phân thức được xác định khi và chỉ khi x2 - 5x + 6 ≠ 0
⇔ ( x - 3 )( x - 2 ) ≠ 0 hay x ≠ 2,x ≠ 3.
+ Giá trị của phân thức được xác định khi và chỉ khi x - 3 ≠ 0 hay x ≠ 3.
Với x ≠ 2,x ≠ 3 ta có: 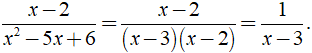
Vậy với x ≠ 2,x ≠ 3 ta có: 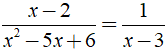
Câu 7:
 Xem đáp án
Xem đáp án
Chọn đáp án C.
Ta có:
+ 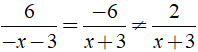
⇒ Đáp án A sai.
+ 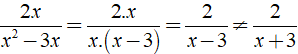
⇒ Đáp án B sai.
+ 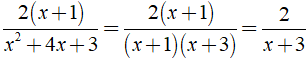
⇒ Đáp án C đúng.
+ 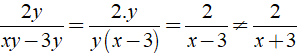
⇒ Đáp án D sai.
Câu 8:
Điền vào chỗ trống đa thức sao cho 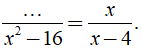
 Xem đáp án
Xem đáp án
Chọn đáp án B.
Gọi A là đa thức cần tìm thỏa mãn A( x - 4 ) = x( x2 - 16 )
Ta có: A( x - 4 ) = x( x - 4 )( x + 4 ) ⇒ A = x( x + 4 ) = x2 + 4x
Câu 9:
 Xem đáp án
Xem đáp án
Chọn đáp án B.
Điều kiện xác định là x ≠ 0;y ≠ 0.
Ta có ==
Câu 10:
 Xem đáp án
Xem đáp án
Chọn đáp án C.
Điều kiện xác định là x ≠ 0;x ≠ 4
Ta có
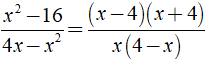
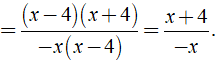
Câu 11:
Rút gọn biểu thức 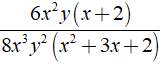
 Xem đáp án
Xem đáp án
Chọn đáp án B.
Điều kiện xác định x,y ≠ 0;x2 + 3x + 2 ≠ 0
Ta có
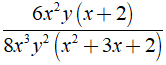
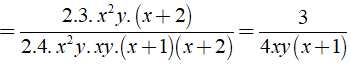
Câu 12:
Rút gọn phân thức 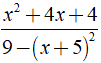 được kết quả là ?
được kết quả là ?
 Xem đáp án
Xem đáp án
Chọn đáp án A.
Điều kiện xác định: 9 - ( x + 5 )2 ≠ 0.
Ta có:
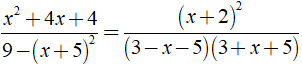
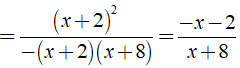
Câu 13:
 Xem đáp án
Xem đáp án
Chọn đáp án D.
Ta có:
+ 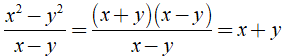
⇒ Đáp án A đúng.
+ 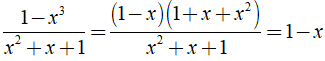
⇒ Đáp án B đúng.
+ 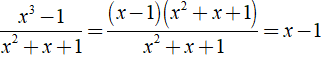
⇒ Đáp án C đúng.
+ 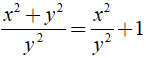
⇒ Đáp án D sai.
Câu 14:
 Xem đáp án
Xem đáp án
Chọn đáp án D.
Ta có
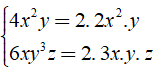
⇒ Mẫu thức chung đơn giản nhất là: 12x2y3z
Câu 15:
 Xem đáp án
Xem đáp án
Chọn đáp án B.
Ta có:
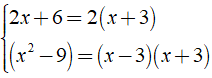
Câu 16:
 Xem đáp án
Xem đáp án
Chọn đáp án A.
Ta có:
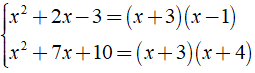
⇒ MTC = ( x + 3 )( x + 4 )( x - 1 )
MTC = ( x - 1 )( x2 + 7x + 10 ) = x3 + 7x2 + 10x - x2 - 7x - 10
= x3 + 6x2 + 3x - 10.
Câu 17:
Kết quả của phép cộng 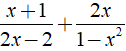
 Xem đáp án
Xem đáp án
Chọn đáp án B.
Ta có:
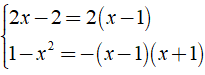
⇒ MTC = - 2( x - 1 )( x + 1 ).
Khi đó ta có:
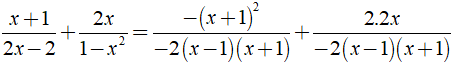
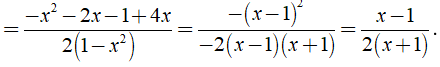
Câu 21:
Rút gọn biểu thức 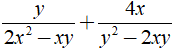 được kết quả là ?
được kết quả là ?
 Xem đáp án
Xem đáp án
Chọn đáp án C.
Ta có:
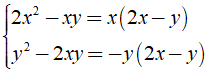
⇒ MTC = - xy( 2x - y ).
Khi đó ta có:
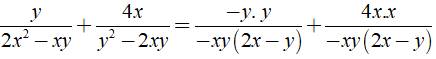
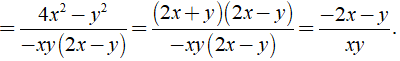
Câu 24:
Thức hiện phép trừ phân thức 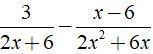 được kết quả là ?
được kết quả là ?
 Xem đáp án
Xem đáp án
Chọn đáp án C.
Ta có:
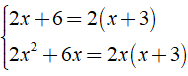
⇒ MTC = 2x( x + 3 )
Khi đó ta có:
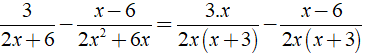
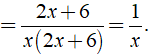
Câu 26:
Rút gọn biểu thức 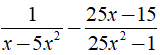 được kết quả là
được kết quả là
 Xem đáp án
Xem đáp án
Chọn đáp án A.
+ 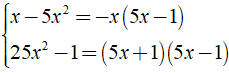
⇒ MTC = - x( 5x + 1 )( 5x - 1 ).
Khi đó ta có:
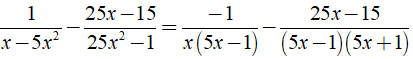
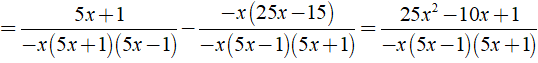
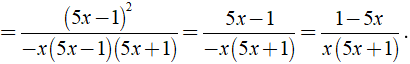
Câu 38:
 Xem đáp án
Xem đáp án
Giá trị của phân thức xác định khi và chỉ khi 2x + 4 ≠ 0 ⇔ x ≠ - 2.
Câu 39:
Giá trị của biểu thức 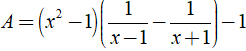 tại x = 1 là ?
tại x = 1 là ?
 Xem đáp án
Xem đáp án
Chọn đáp án D.
Ta có:
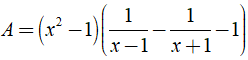
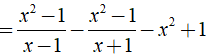
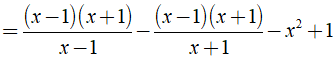
= x + 1 - x + 1 - x2 + 1 = 3 - x2.
Với x = 1 ta có A = 3 - 12 = 2.
Câu 40:
Tìm điều kiện xác định của phân thức
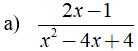
 Xem đáp án
Xem đáp án
a) Phân thức 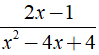 xác định ⇔ x2 - 4x + 4 ≠ 0
xác định ⇔ x2 - 4x + 4 ≠ 0
⇔ ( x - 2 )2 ≠ 0 ⇒ x ≠ 2 (vì ( x - 2 )2 ≥ 0 )
Vậy điều kiện xác định của phân thức 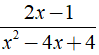 là x ≠ 2.
là x ≠ 2.
Câu 41:
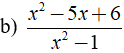
 Xem đáp án
Xem đáp án
b) Phân thức 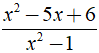 xác định ⇔ x2 - 1 ≠ 0
xác định ⇔ x2 - 1 ≠ 0
⇔ ( x - 1 )( x + 1 ) ≠ 0 ⇔ x ≠ ± 1.
Vậy điều kiện xác định của phân thức 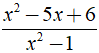 là x ≠ ± 1.
là x ≠ ± 1.
Câu 42:
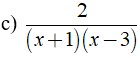
 Xem đáp án
Xem đáp án
c) Phân thức 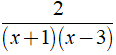 xác định ⇔ ( x + 1 )( x - 3 ) ≠ 0
xác định ⇔ ( x + 1 )( x - 3 ) ≠ 0
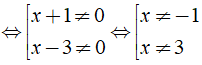
Vậy điều kiện xác định của phân thức 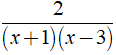 là x ≠ - 1 hoặc x ≠ 3
là x ≠ - 1 hoặc x ≠ 3
Câu 43:
Chứng minh các phân thức sau bằng nhau
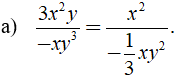
 Xem đáp án
Xem đáp án
a) Ta có 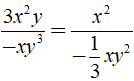
Vì 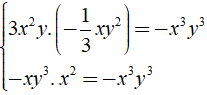
⇒ 3x2y.( (- 1/3)xy2 ) = - xy3.x2
⇒ 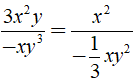
Câu 48:
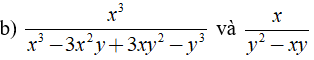
 Xem đáp án
Xem đáp án
b) Ta có
+ x3 - 3x2y + 3xy2 - y3 = ( x - y )3
+ y2 - xy = y( y - x ) = - y( x - y )
⇒ Mẫu thức chung là - y( x - y )3.
Khi đó ta có:
+ 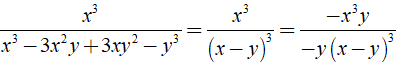
+ 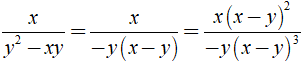
Câu 49:
Thực hiện phép cộng các phân thức sau:
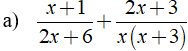
 Xem đáp án
Xem đáp án
a) Ta có:
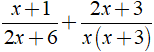
+ 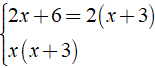
⇒ MTC = 2x( x + 3 )
Khi đó ta có:
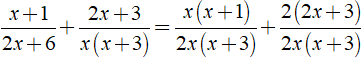
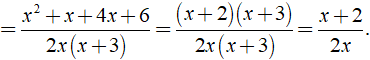
Câu 52:
Rút gọn rồi tính giá trị biểu thức 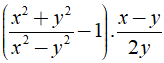 với x = 14 và y = -15
với x = 14 và y = -15
 Xem đáp án
Xem đáp án
Ta có:
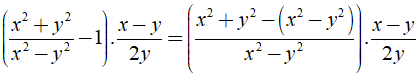
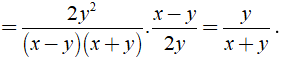
Với x = 14 và y = -15 , ta có:
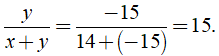
Câu 55:
Xác định giá trị a, b, c để 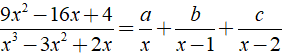
 Xem đáp án
Xem đáp án
Ta có:
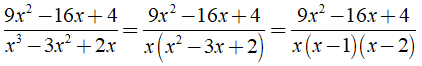
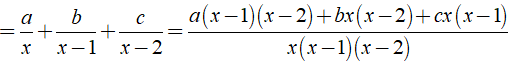
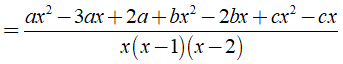
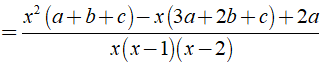
Dùng phương pháp hệ số bất định, khi đó ta có hệ:
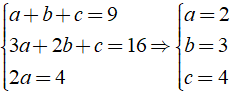
Câu 57:
b) Xác định giá trị a, b để 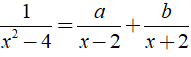
 Xem đáp án
Xem đáp án
b) Ta có:
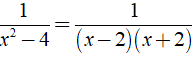
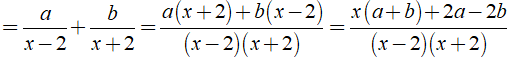
Áp dụng phương pháp hệ số bất định ta có:
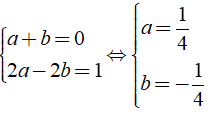
Vậy giá trị a, b cần tìm là a = 1/4, b = -1/4
Câu 58:
a) Xác định giá trị a, b để 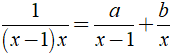
 Xem đáp án
Xem đáp án
a) Ta có:
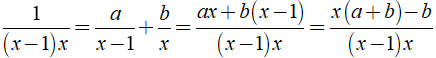
Áp dụng phương pháp hệ số bất định ta có:
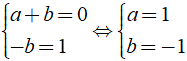
Vậy giá trị a, b cần tìm là a = 1, b = -1
Câu 60:
Xác định giá trị của a, b, c để 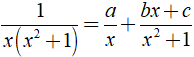
 Xem đáp án
Xem đáp án
Ta có:
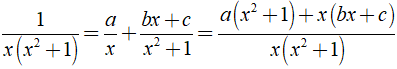
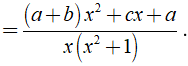
Áp dụng phương pháp hệ số bất định ta có:
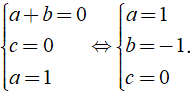
Vậy giá trị a, b, c cần tìm là a = 1, b = -1, c = 0.
Câu 61:
Cho biểu thức 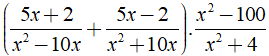
a) Tìm điều kiện của x để giá trị của biểu thức được xác định.
 Xem đáp án
Xem đáp án
a) Giá trị của biểu thức xác định khi mỗi giá trị của phân thức trong biểu thức đều được xác định.
Khi đó điều kiện xác định: x2 - 10x ≠ 0,x2 + 10x ≠ 0,x2 + 4 ≠ 0
+ x2 - 10x ≠ 0 ⇔ x( x - 10 ) ≠ 0 khi x ≠ 0 và x - 10 ≠ 0 hay x ≠ 0,x ≠ 10.
+ x2 + 10x ≠ 0 ⇔ x( x + 10 ) ≠ 0 khi x ≠ 0 và x + 10 ≠ 0 hay x ≠ 0,x ≠ - 10.
+ x2 + 4 > 0 với mọi giá trị của x.
Vậy điều kiện xác định của biểu thức là x ≠ 0,x ≠ ± 10.
Câu 62:
Cho biểu thức 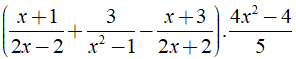
a) Tìm điều kiện giác trị của x để giá trị của biểu thức xác định.
 Xem đáp án
Xem đáp án
a) Giá trị của biểu thức xác định khi mỗi giá trị của phân thức trong biểu thức đều được xác định.
Khi đó điều kiện xác định là: 2x - 2 ≠ 0;x2 - 1 ≠ 0;2x + 2 ≠ 0 hay x ≠ ± 1
Vậy với x ≠ ± 1 thì giá trị của biểu thức xác định.
Câu 63:
b) Chứng minh rằng khi giá trị của biểu thức xác định thì giá trị của nó không phụ thuộc vào biến x
 Xem đáp án
Xem đáp án
b) Ta có:
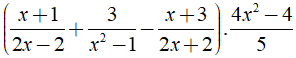
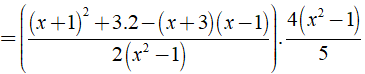
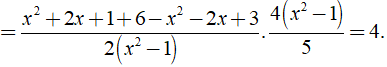
⇒ Giá trị của biểu thức A không phụ thuộc vào biến x
Câu 64:
Cho a3 + b3 + c3 = 3abc và a + b + c ≠ 0. Tính giá trị của biểu thức 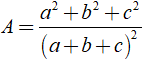
 Xem đáp án
Xem đáp án
Ta có: a3 + b3 + c3 = 3abc ⇔ a3 + b3 + c3 - 3abc = 0
⇔ ( a + b )3 + c3 - 3ab( a + b ) - 3abc = 0
⇔ ( a + b )3 + c3 - 3ab( a + b + c ) = 0
⇔ ( a + b + c )3 - 3( a + b )c( a + b + c ) - 3ab( a + b + c ) = 0
⇔ ( a + b + c )( a2 + b2 + c2 - ab - bc - ca ) = 0
⇒ a2 + b2 + c2 - ab - bc - ca = 0 (vì a + b + c ≠ 0. )
⇔ a2 + b2 + c2 = ab + bc + ca.
Khi đó ta có:
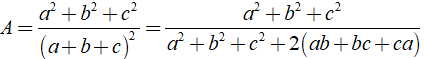
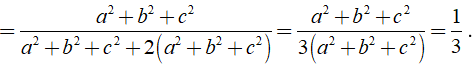
Vậy A= 1/3

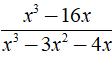
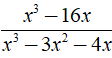
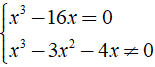
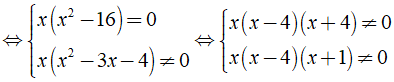
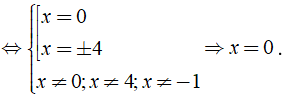
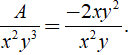
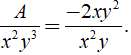
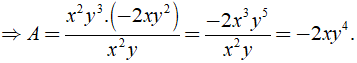
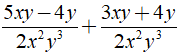
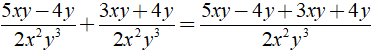
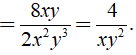
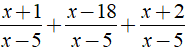
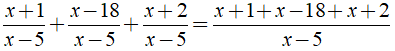
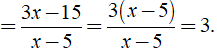
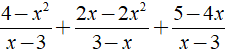
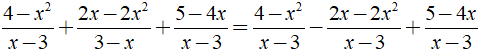
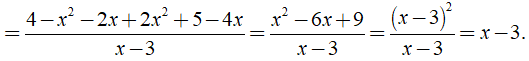
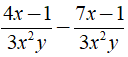
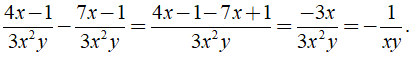
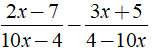
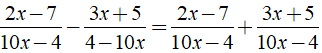
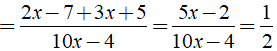
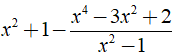
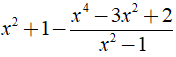
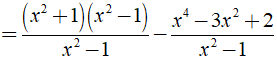
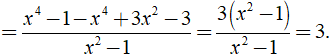
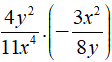
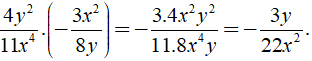
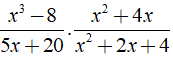
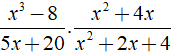
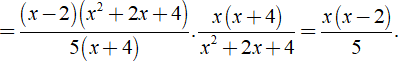
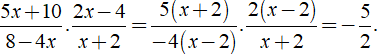
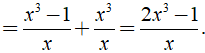
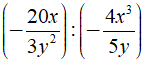
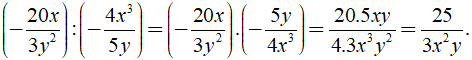
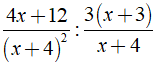
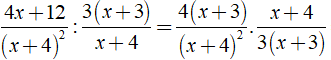
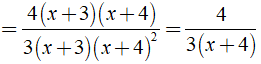
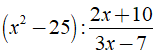
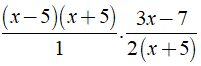
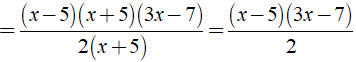
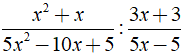
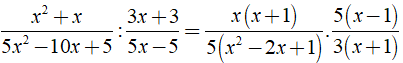
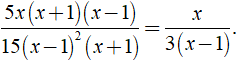
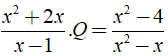
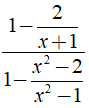
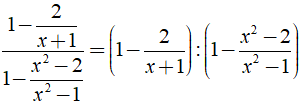
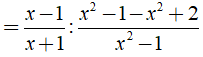
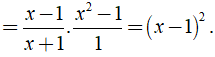
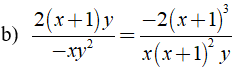
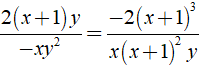
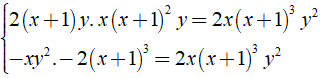
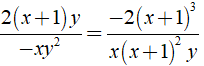
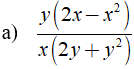
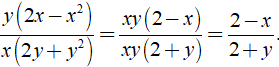
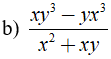
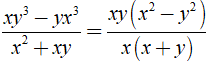
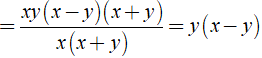
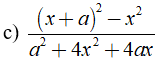
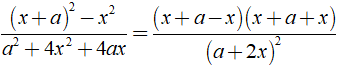
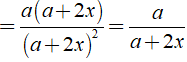
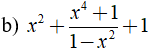
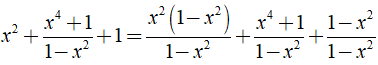
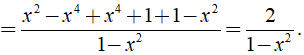
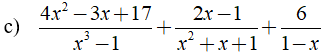
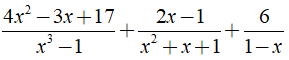
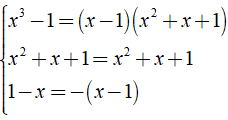
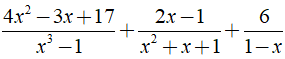
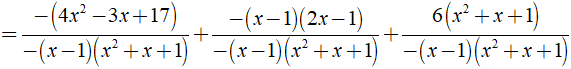
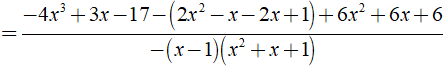
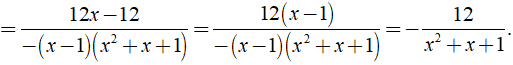
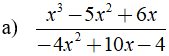
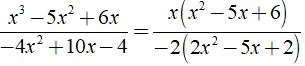
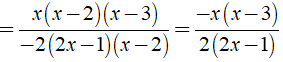
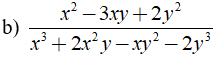
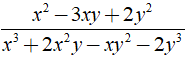
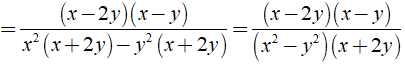
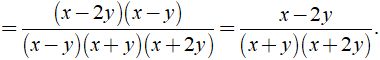
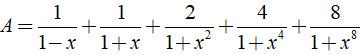
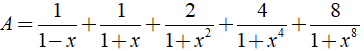
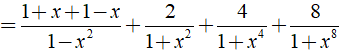
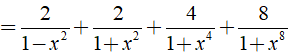
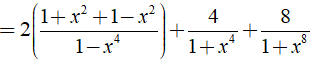
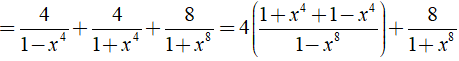
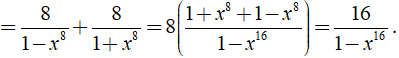
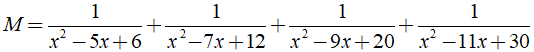
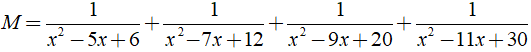
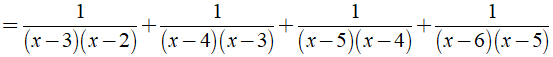
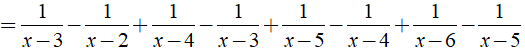
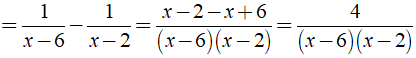
![Rút gọn biểu thức A= 3/ (1 .2)^2 + 5/ (2 .3)^2 + .... + 2n+ 1/ [n (n +1)]^2 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/08/blobid155-1660922169.png)
![Rút gọn biểu thức A= 3/ (1 .2)^2 + 5/ (2 .3)^2 + .... + 2n+ 1/ [n (n +1)]^2 (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2022/08/blobid154-1660922122.png)
![Rút gọn biểu thức A= 3/ (1 .2)^2 + 5/ (2 .3)^2 + .... + 2n+ 1/ [n (n +1)]^2 (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2022/08/blobid153-1660922119.png)
![Rút gọn biểu thức A= 3/ (1 .2)^2 + 5/ (2 .3)^2 + .... + 2n+ 1/ [n (n +1)]^2 (ảnh 4)](https://video.vietjack.com/upload2/quiz_source1/2022/08/blobid152-1660922117.png)
![Rút gọn biểu thức A= 3/ (1 .2)^2 + 5/ (2 .3)^2 + .... + 2n+ 1/ [n (n +1)]^2 (ảnh 5)](https://video.vietjack.com/upload2/quiz_source1/2022/08/blobid151-1660922115.png)
![Rút gọn biểu thức A= 3/ (1 .2)^2 + 5/ (2 .3)^2 + .... + 2n+ 1/ [n (n +1)]^2 (ảnh 6)](https://video.vietjack.com/upload2/quiz_source1/2022/08/blobid150-1660922111.png)