15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 8 KNTT Bài 13. Hình chữ nhật có đáp án

Câu 1:

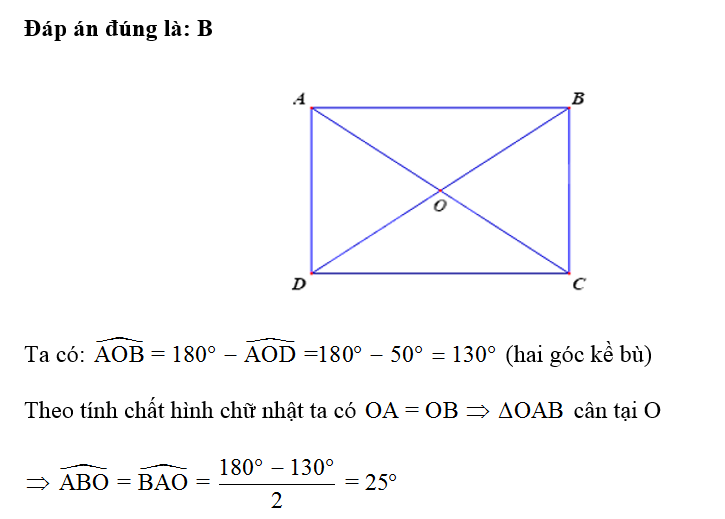
Hai đường chéo của hình chữ nhật có tính chất nào sau đây?

A. Chúng vuông góc với nhau.

B. Chúng bằng nhau.

C. Chúng cắt nhau tại trung điểm của mỗi đường.

D. Chúng bằng nhau và cắt nhau tại trung điểm của mỗi đường.

Xem đáp án

Đáp án đúng là: D

Hai đường chéo của hình chữ nhật bằng nhau và cắt nhau tại trung điểm của mỗi đường.

Câu 2:

Khẳng định nào sau đây là đúng?

A. Hình chữ nhật là tứ giác có bốn cạnh bằng nhau.

B. Hình chữ nhật là tứ giác có bốn góc vuông.

C. Hình chữ nhật là tứ giác có hai góc vuông.

D. Hình chữ nhật là tứ giác có hai đường chéo bằng nhau.

Xem đáp án

Đáp án đúng là: B

Hình chữ nhật là tứ giác có bốn góc vuông.

Câu 3:

Khẳng định nào sau đây là sai?

A. Hình chữ nhật có hai đường chéo bằng nhau.

B. Hình chữ nhật có hai đường chéo cắt nhau tại trung điểm mỗi đường.

C. Hình chữ nhật có hai cạnh kề bằng nhau.

D. Trong hình chữ nhật, giao của hai đường chéo là tâm của hình chữ nhật đó.

Xem đáp án

Đáp án đúng là: C

Hình chữ nhật có hai cạnh kề bằng nhau là khẳng định sai.

Câu 4:

Hình bình hành ABCD là hình chữ nhật khi

A. AB = AD.

B. $\hat{A} = 90 °$

C. AB = 2AC

D.

\hat{A} = \hat{C}

Xem đáp án

Đáp án đúng là: B

Hình bình hành có một góc vuông là hình chữ nhật.

Câu 5:

Chọn câu sai.

Tứ giác ABCD là hình chữ nhật khi

A. $\hat{A} = \hat{B} = \hat{C} = 90 °$

B. $\hat{A} = \hat{B} = \hat{C} = 90 °$ và AB // CD

C. AB = CD = AD = BC

D. AB // CD; AB = CD; AC = BD

Xem đáp án

Đáp án đúng là: C

+ Ta thấy AB = CD = AD = BC thì ABCD chỉ có bốn cạnh bằng nhau nên ABCD chưa chắc là hình chữ nhật .

Nếu $\hat{A} = \hat{B} = \hat{C} = 90 °$ thì tứ giác ABCD có ba góc vuông nên ABCD là hình chữ nhật (do dấu hiệu tứ giác có 3 góc vuông).

+ Nếu $\hat{A} = \hat{B} = \hat{C} = 90 °$ và AB // CD thì tứ giác ABCD có AD // BC; AB // CD nên ABCD là hình bình hành, lại có nên ABCD là hình chữ nhật. (do dấu hiệu hình bình hành có một góc vuông)

+ Nếu AB // CD; AB = CD và AC = BD thì ABCD là hình bình hành (do có cặp cạnh đối AB; CD song song và bằng nhau), lại có hai đường chéo bằng nhau AC = BD nên ABCD là hình chữ nhật (do dấu hiệu hình bình hành có hai đường chéo bằng nhau).

Câu 6:

Hãy chọn câu đúng. Cho với M thuộc cạnh BC. Từ M vẽ ME song song với AB và MF song song với AC. Hãy xác định điều kiện của $Δ A B C$ để tứ giác AEMF là hình chữ nhật.

A. $Δ A B C$ vuông tại A

B. $Δ A B C$ vuông tại B

C. $Δ A B C$ vuông tại C

D. $Δ A B C$ đều

Xem đáp án

Hãy chọn câu đúng. Cho với M thuộc cạnh BC. Từ M vẽ ME song song với AB và MF song song với AC. Hãy xác định điều (ảnh 1)

Câu 7:

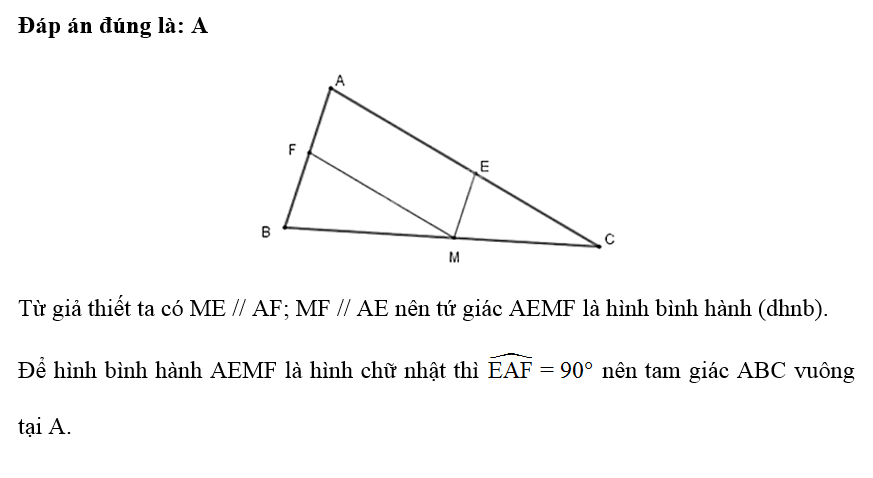
Cho tam giác ABC vuông tại A, điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là chân đường vuông góc kẻ từ M đến AB, AC. Điểm M ở vị trí nào trên BC thì DE có độ dài nhỏ nhất?

A. M là hình chiếu của A trên BC

B. M là trung điểm của BC

C. M trùng với B

D. Đáp án khác

Xem đáp án

Đáp án đúng là: C

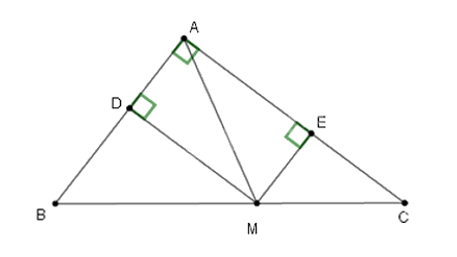
Cho tam giác ABC vuông tại A, điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là chân đường vuông góc kẻ từ M đến AB (ảnh 1)

Xét tứ giác ADME có $\hat{A} = \hat{ADM} = \hat{AEM} = 90 °$ nên ADME là hình chữ nhật.

Vì ADME là hình chữ nhật nên AM = DE (tính chất)

Để DE nhỏ nhất thì AM nhỏ nhất mà AM nhỏ nhất khi M là hình chiếu của A trên BC

Từ đó DE nhỏ nhất khi M là hình chiếu của A trên BC.

Hình chữ nhật có hai đường chéo bằng nhau.

Câu 8:

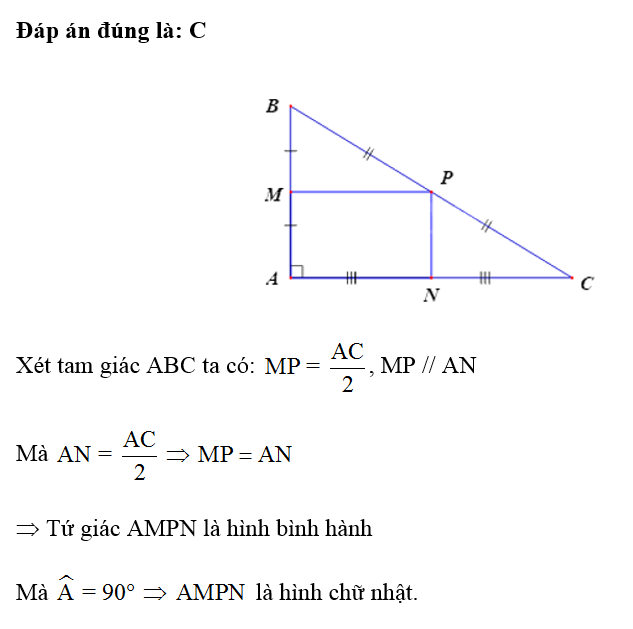
Cho tam giác ABC, đường cao AH. I là trung điểm của AC, E đối xứng với H qua I. Tứ giác AHCE là hình gì?

A. Hình thang.

B. Hình thang cân.

C. Hình thang vuông.

D. Hình chữ nhật.

Xem đáp án

Đáp án đúng là: D

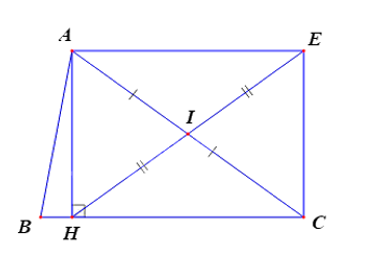
Cho tam giác ABC, đường cao AH. I là trung điểm của AC, E đối xứng với H qua I. Tứ giác AHCE là hình gì? (ảnh 1)

Tứ giác AHCE là hình bình hành vì IA = IC, IH = IE.

Mà $\hat{H} = 90 ° \Rightarrow A H C E$ là hình chữ nhật.

Hình bình hành có một góc vuông là hình chữ nhật

Câu 9:

Hình chữ nhật ABCD có O là giao điểm của hai đường chéo. Biết $\hat{AOD} = 50 °,$ tính số đo $\hat{ABO}$

A. 50°.

B. 25°.

C. 90°.

D. 130°.

Xem đáp án

Hình chữ nhật ABCD có O là giao điểm của hai đường chéo. Biết góc AOD= 50 độ tính số đo góc ABO (ảnh 1)

Câu 10:

Cho tam giác ABC vuông tại A. Gọi M, N, P lần lượt là trung điểm thuộc các cạnh AB, AC, BC và $MP = \frac{AC}{2}$ , MP // AN. Tứ giác AMPN là hình gì?

A. Hình thang.

B. Hình thang cân.

C. Hình chữ nhật.

D. Hình thang vuông.

Xem đáp án

Cho tam giác ABC vuông tại A. Gọi M, N, P lần lượt là trung điểm thuộc các cạnh AB, AC, BC (ảnh 1)

Câu 11:

Cho hình chữ nhật ABCD. E, F, G, H là trung điểm của các cạnh AB, BC, CD, DA và EF // AC, GH // AC; EH // BD, FG // BD. Tứ giác EFGH là hình gì?

A. Hình chữ nhật.

B. Hình thang cân.

C. Hình thang.

D. Hình bình hành.

Xem đáp án

Đáp án đúng là: D

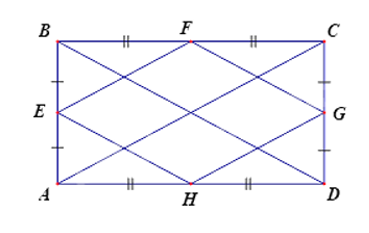
Cho hình chữ nhật ABCD. E, F, G, H là trung điểm của các cạnh AB, BC, CD, DA và EF // AC, GH // AC; (ảnh 1)

Tứ giác EFGH là hình bình hành vì

+ EF // GH (EF // AC, GH // AC)

+ EH // FG (EH // BD, FG // BD)

Câu 12:

Cho tam giác ABC vuông tại A, AC = 6cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Chu vi của tứ giác ADME bằng:

A. 6cm

B. 36cm

C. 18cm

D. 12cm

Xem đáp án

Cho tam giác ABC vuông tại A, AC = 6cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông (ảnh 1)

Câu 13:

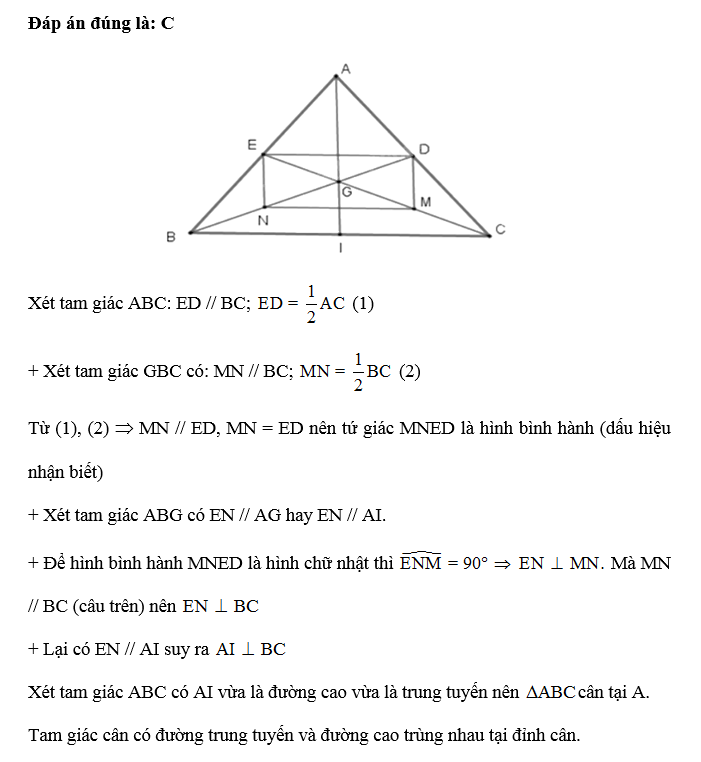
Cho tam giác ABC với ba trung tuyến AI, BD, CE đồng quy tại G sao cho ED // BC; $ED = \frac{1}{2} AC$ .M và N lần lượt là các điểm của GC và GB và MN // BC; $MN = \frac{1}{2} BC$ . Tứ giác MNED là hình gì?

A. Hình chữ nhật

B. Hình bình hành

C. Hình thang cân

D. Hình thang vuông

Xem đáp án

Đáp án đúng là: B

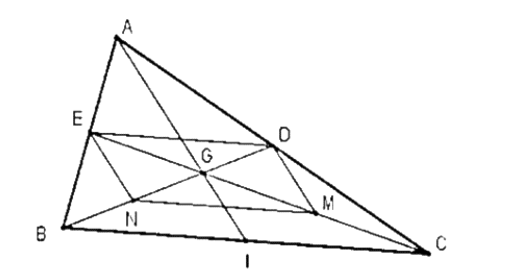
Cho tam giác ABC với ba trung tuyến AI, BD, CE đồng quy tại G sao cho ED // BC (ảnh 1)

Xét tam giác ABC : ED // BC; $ED = \frac{1}{2} AC$ (1)

+ Xét tam giác GBC có : MN // BC; $MN = \frac{1}{2} BC$ (2)

Từ (1), (2) Þ MN // ED, MN = ED nên tứ giác MNED là hình bình hành (dấu hiệu nhận biết)

Câu 14:

Cho tam giác ABC với ba trung tuyến AI, BD, CE đồng quy tại G sao cho ED // BC;

ED = \frac{1}{2} AC

. M và N lần lượt là các điểm của GC và GB và MN // BC;

MN = \frac{1}{2} BC

. Để MNED là hình chữ nhật thì tam giác ABC cần có điều kiện:

A. đều

B. vuông tại A

C. cân tại A

D. vuông cân tại A

Xem đáp án

Câu 15:

Cho tứ giác ABCD. E, F, G, H là trung điểm của các cạnh AB, BC, CD, DA và EF // AC, GH // AC, EH // BD, FG // BD. Tứ giác ABCD cần thêm điều kiện nào sau đây để tứ giác EFGH là hình chữ nhật?

A. AC = BD .

B. $A C ⊥ B D$

C. AB = BC.

D. AB // CD .

Xem đáp án