15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 8 KNTT Bài 11. Hình thang cân có đáp án

Câu 1:

Trong các khẳng định sau, khẳng định nào sai?

A. Tứ giác có hai cạnh bên bằng nhau là hình thang cân.

B. Hình thang cân có hai cạnh bên bằng nhau.

C. Hình thang cân có hai góc đối bù nhau.

D. Hình thang cân có hai góc kề một cạnh đáy bằng nhau.

Xem đáp án

Đáp án đúng là: A

Dựa vào tính chất hình thang cân: Tứ giác có hai cạnh bên bằng nhau là hình thang cân là khẳng định sai.

Câu 2:

Hình thang cân là hình thang có

A. hai góc kề bằng nhau.

B. hai góc đối bằng nhau.

C. hai cạnh đối bằng nhau.

D. hai đường chéo bằng nhau.

Xem đáp án

Đáp án đúng là: D

Theo tính chất của hình thang cân: Hình thang cân là hình thang có hai đường chéo bằng nhau.

Câu 3:

Tứ giác ABCD có AB // CD là một hình thang, ta gọi

A. các đoạn thẳng AB và CD là các cạnh bên.

B. các đoạn thẳng AB và CD là các cạnh đáy.

C. các đoạn thẳng AB và CD là các đường chéo.

D. các đoạn thẳng AB và CD là các đường cao.

Xem đáp án

Đáp án đúng là: B

Hình thang ABCD có AB // CD ta gọi các đoạn thẳng AB và CD là các cạnh đáy.

Câu 4:

Cho hình vẽ, số đo $\hat{BCD}$ bằng:

Cho hình vẽ, số đo góc BCD bằng: (ảnh 1)

A. 70°

B. 110°

C. 80°

D. 140°

Xem đáp án

Đáp án đúng là: A

Tứ giác ABCD có $\hat{A} + \hat{D} = 110 ° + 70 ° = 180 °$ nên AB // CD suy ra ABCD là hình thang.

Mặt khác ta có: $\hat{ABC} = 180 ° - 70 ° = 110 °$

Hình thang ABCD có $\hat{A} = \hat{B} = 110 ° .$ Suy ra ABCD là hình thang cân

Suy ra: $\hat{C} = \hat{D} = 70 °$

Câu 5:

Cho hình thang cân ABCD có AB // CD và AC = 12 cm, AB = 6 cm. Độ dài BD là

A. 12 cm

B. 13 cm

C. 7 cm

D. 6 cm

Xem đáp án

Đáp án đúng là: A

Vì ABCD là hình thang cân có AB // CD nên $B D = A C = 12 c m$ (hình thang cân có hai đường chéo bằng nhau).

Câu 6:

Cho hình thang cân ABCD có AB // CD. Gọi M là giao điểm của AC và BC. Tam giác MCD là tam giác gì?

A. Tam giác cân

B. Tam giác nhọn

C. Tam giác vuông

D. Tam giác tù

Xem đáp án

Đáp án đúng là: A

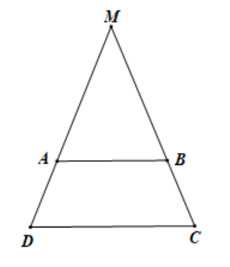
Cho hình thang cân ABCD có AB // CD. Gọi M là giao điểm của AC và BC. Tam giác MCD là (ảnh 1)

Vì ABCD là hình thang cân có hai đáy là AB và CD nên $\hat{C} = \hat{D}$

Mặt khác xét tam giác MCD có $\hat{C} = \hat{D}$ . Suy ra tam giác MCD là tam giác cân.

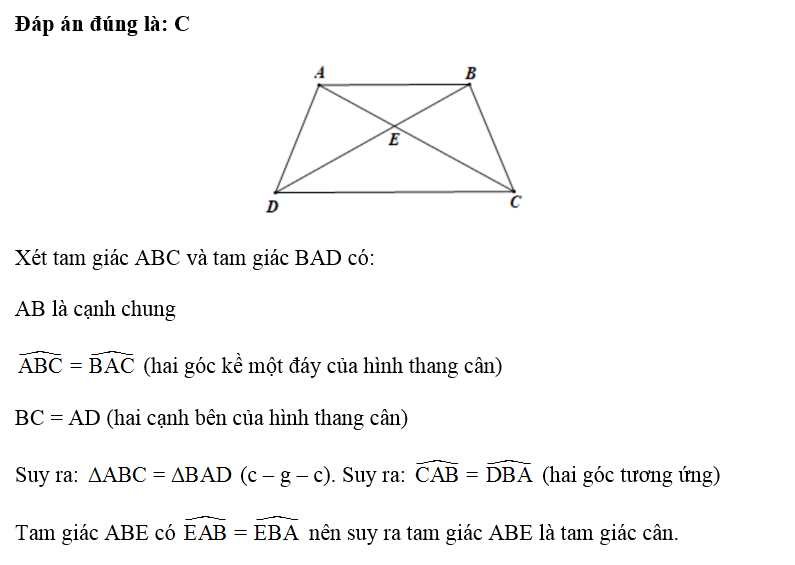
Câu 7:

Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD. Tìm khẳng định sai trong các khẳng định sau:

A. ABCD là hình thang cân

B. AC = BD

C. BC = AD

D. Tam giác AOD cân tại C.

Xem đáp án

Đáp án đúng là: A

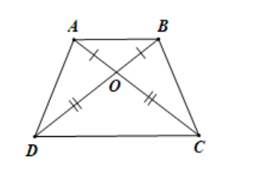
Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD. Tìm khẳng định sai trong các khẳng định sau: (ảnh 1)

Ta có: $O A = O B; O C = O D \Rightarrow O A + O C = O B + O D \Rightarrow A C = B D$

Hình thang ABCD (AB // CD) có AC = BD nên ABCD là hình thang cân

Suy ra: BC = AD

Câu 8:

Hình thang cân có một góc bằng 50°. Hiệu giữa hai góc kề một cạnh bên là:

A. 130°

B. 100°

C. 80°

D. 50°

Xem đáp án

Đáp án đúng là: C

Hình thang cân có một góc bằng 50°. Hiệu giữa hai góc kề một cạnh bên là: (ảnh 1)

Giả sử ABCD là hình thang có đáy lớn là DC; đáy nhỏ là AB; $\hat{C} = \hat{D} = 50 °$ . Khi đó:

$\hat{A} = \hat{B} = \frac{360 ° - \hat{C} - \hat{D}}{2} = \frac{360 ° - 50 ° - 50 °}{2} = 130 °$

$\Rightarrow \hat{B} - \hat{C} = \hat{A} - \hat{D} = 130 ° - 50 ° = 80 °$

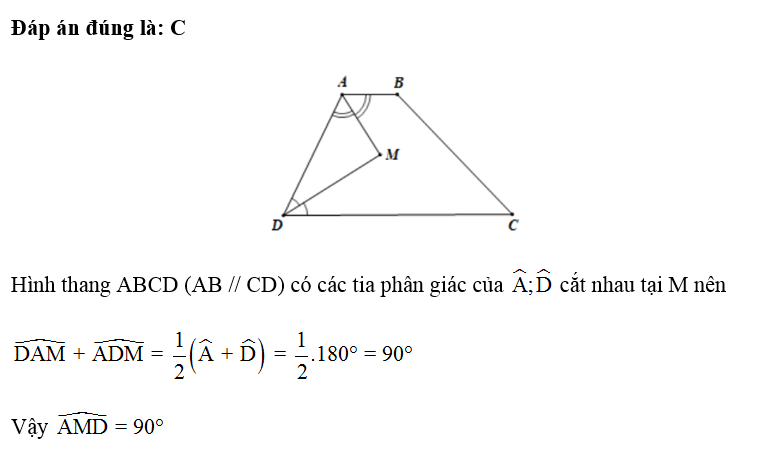
Câu 9:

Cho hình thang ABCD (AB // CD) biết $\hat{A} = 58 °$ thì:

A. $\hat{D} = 122 °$

B. $\hat{D} = 212 °$

C. $\hat{D} = 22 °$

D.

\hat{D} = 0 °

Xem đáp án

Đáp án đúng là: A

Hình thang ABCD (AB // CD) nên $\hat{A} + \hat{D} = 180 °$

Mà $\hat{A} = 58 °$ nên $58 ° + \hat{D} = 180 ° \Rightarrow \hat{D} = 180 ° - 58 ° = 122 °$

Câu 10:

Trong hình thang có hai góc tù:

A. hai góc còn lại cũng là góc tù.

B. hai góc còn lại là hai góc vuông.

C. hai góc còn lại gòm một góc tù và một góc nhọn

D. hai góc còn lại là hai góc nhọn.

Xem đáp án

Đáp án đúng là: C

Trong hình thang có hai góc tù: A. hai góc còn lại cũng là góc tù. (ảnh 1)

Xét hình thang ABCD có AB // CD nên $\hat{A} + \hat{D} = 180 °$ (2 góc trong cùng phía) suy ra hai góc đó có nhiều nhất một góc nhọn, có nhiều nhất một góc tù.

Tương tự $\hat{B}$ và $\hat{C}$ cũng vậy.

Do đó trong bốn góc A, B, C, D có hai góc tù thì hai góc còn lại là hai góc nhọn.

Câu 11:

Cho hình thang cân ABCD (AB // CD). Tìm khẳng định sai trong các khẳng định sau:

A. $ΔABC = ΔBAD$

B. $\hat{CBA} = \hat{DBA}$

C. $ΔABE$ cân

D.

ΔAED

cân

Xem đáp án

Cho hình thang cân ABCD (AB // CD). Tìm khẳng định sai trong các khẳng định sau: (ảnh 1)

Câu 12:

Cho tam giác ABC cân tại A. các điểm D và E lần lượt trên các cạnh AB, AC sao cho DE // BC. Tìm khẳng định đúng:

A. BE = DC

B. BE = DE

C. DC = DE

D. DC = BC

Xem đáp án

Đáp án đúng là: A

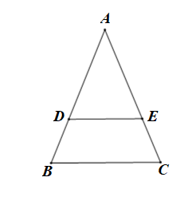
Cho tam giác ABC cân tại A. các điểm D và E lần lượt trên các cạnh AB, AC sao cho DE // BC. Tìm khẳng định đúng: (ảnh 1)

Tứ giác DBCE có DE // BC nên DBCE là hình thang

Hình thang DBCE có $\hat{B} = \hat{C}$ nên DBCE là hình thang cân

Suy ra: BE = DC

Câu 13:

Cho hình thang cân ABCD (AB // CD) đáy nhỏ AB = 3 cm, đường cao AH = 5 cm. Biết $\hat{D} = 45 °$ . Độ dài đáy lớn CD là:

A. 8cm

B. 11 cm

C. 12 cm

D. 13 cm

Xem đáp án

Đáp án đúng là: D

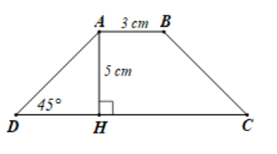
Cho hình thang cân ABCD (AB // CD) đáy nhỏ AB = 3 cm, đường cao AH = 5 cm (ảnh 1)

Ta có tam giác AHD vuông cân tại H vì $\hat{D} = 45 °$ . Do đó DH = AH = 5 cm

Mà CD = AB + 2DH $\Rightarrow CD = 3 + 2.5 = 13cm$

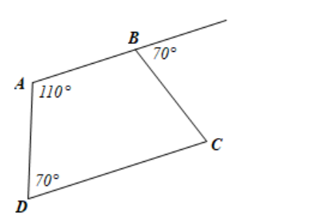
Câu 14:

Cho hình vẽ sau, tính các góc A, C của hình thang ABCD (AB // CD) biết:

A. $\hat{A} = \hat{C} = 111 °$

B. $\hat{A} = \hat{C} = 130 °$

C. $\hat{A} = 111 °; \hat{C} = 130 °$

D.

\hat{A} = 130 °; \hat{C} = 111 °

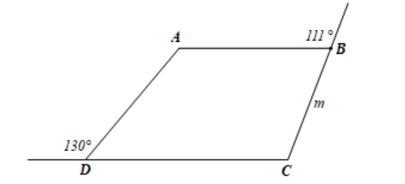
Xem đáp án

Đáp án đúng là: D

Hình thang ABCD có AB // CD nên $\hat{A} = \hat{ADE} = 130 °; \hat{C} = \hat{ABF} = 111 °$

Câu 15:

Hình thang ABCD (AB // CD) có các tia phân giác của $\hat{A}; \hat{D}$ cắt nhau tại M thì

A. $\hat{AMD} = 180 °$

B. $\hat{AMD} = 150 °$

C. $\hat{AMD} = 90 °$

D.

\hat{AMD} = 60 °

Xem đáp án