12 câu hỏi trắc nghiệm thuộc Đề thi Học kì 1 Toán lớp 8 cực hay, có đáp án (Đề 1)

Top 4 Đề thi Toán 8 Học kì 1 có đáp án, cực sát đề chính thức

Đề thi Học kì 1 Toán lớp 8 cực hay, có đáp án (Đề 1)

3869 lượt thi
12 câu hỏi
90 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Phần trắc nghiệm (2 điểm)

Gía trị của x thỏa mãn x2 + 16 = 8x là

A. x = 8

B. x = 4

C. x = -8

D. x= -4

Xem đáp án

Chọn B

Câu 2:

Kết quả phép tính: $15 x^{3} y^{5} z : 3 x y^{2} z$ là

A. $5 x^{2} y^{3}$

B. 5xy

C. $3 x^{2} y^{3}$

D. 5xyz

Xem đáp án

Chọn A

Câu 3:

Kết quả phân tích đa thức $- x^{2} + 4 x - 4$ là:

A. $- {(x + 2)}^{2}$

B. $- {(x - 2)}^{2}$

C. ${(x - 2)}^{2}$

D. ${(x + 2)}^{2}$

Xem đáp án

Chọn B

Câu 4:

Mẫu thức chung của 2 phân thức: $\frac{x + 5}{x - x^{2}} + \frac{x - 3}{2 - 4 x + 2 x^{2}}$ là:

A. $2 {(x - 1)}^{2}$

B. $x {(x - 1)}^{2}$

C. $2 x (x - 1)$

D. $2 x {(x - 1)}^{2}$

Xem đáp án

Chọn D

Câu 5:

Điều kiện xác định của phân thức: $\frac{3 x + 4}{9 x^{2} - 1}$ là:

A. x≠1/3

B. x≠±1/3

C. x≠-1/3

D. x≠9

Xem đáp án

Chọn B

Câu 6:

Khẳng định nào sau đây là sai:

A. Tứ giác có 2 đường chéo vuông góc với nhau tại trung điểm mỗi đường là hình thoi.

B. Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành

C. Hình chữ nhật có 2 đường chéo bằng nhau là hình vuông.

D. Hình chữ nhật có 2 đường chéo vuông góc với nhau là hình vuông.

Xem đáp án

Chọn C

Câu 7:

Cho tứ giác MNPQ. Gọi E, F , G, H lần lượt là trung điểm các cạnh MN, NP, PQ, QM. Tứ giác EFGH là hình thoi nếu 2 đường chéo MP, NQ của tứ giác MNPQ:

A. Bằng nhau

B. Vuông góc

C. Vuông góc với nhau tại trung điểm mỗi đường

D. Cắt nhau tại trung điểm mỗi đường.

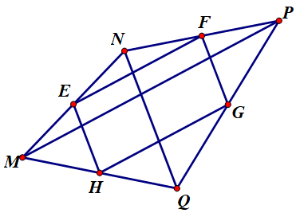
Xem đáp án

Chọn A

Câu 8:

Độ dài 2 đường chéo của hình thoi lần lượt là 6 cm và 4 cm. Độ dài cạnh của hình thoi là:

A. 13 cm

B. $\sqrt{13} c m$

C. 52 cm

D. $\sqrt{52} c m$

Xem đáp án

Chọn B

Câu 9:

Phần tự luận (8 điểm)

Phân tích thành nhân tử:

$a) x^{2} + 4 y^{2} + 4 x y - 16 b) 5 x^{2} - 10 x y + 5 y^{2}$

Xem đáp án

a) x2 + 4y2 + 4xy – 16 = (x + 2y)2 -16 = (x + 2y – 4)(x + 2y + 4).

b) 5x2 - 10xy + 5y2 = 5(x2 - 2xy + y2) = 5(x - y)2

Câu 10:

Cho biểu thức $A = (\frac{x}{x^{2} - 4} + \frac{2}{2 - x} + \frac{1}{x + 2}) . \frac{x + 2}{2}$

a) Tìm điều kiện của x để biểu thức A xác định.

b) Rút gọn A

c) Tính giá trị của A khi x= -1

Xem đáp án

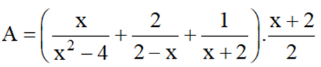
a) x2 - 4 ≠ 0 ⇔ (x + 2)(x - 2) ≠ 0

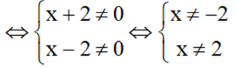
ĐKXĐ: x ≠ - 2 và x ≠ 2

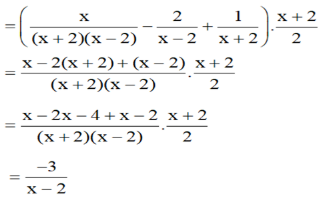
Câu 11:

Cho a + b = 1. Tính giá trị của các biểu thức sau:

$M = a^{3} + b^{3} + 3 a b (a^{2} + b^{2}) + 6 a^{2} b^{2} (a + b) .$

Xem đáp án

Ta có: a + b = 1

M = a3 + b3 + 3ab(a2 + b2) + 6a2b2(a + b)

= (a + b)3 - 3ab(a + b) + 3ab[(a + b)2 - 2ab] + 6a2 b2 (a + b)

= 1 - 3ab + 3ab(1 - 2ab) + 6a2 b2

= 1 - 3ab + 3ab - 6a2 b2 + 6a2 b2

= 1

Câu 12:

Cho tam giác ABC vuông tại A (AB < AC).Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.

a) Chứng minh tứ giác AMIN là hình chữ nhật.

b) Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ACID là hình thoi.

c) Cho AC = 20cm, BC = 25cm.Tính diện tích ΔABC

d) Đường thẳng BN cắt cạnh DC tại K. Chứng minh: $\frac{D K}{D C} = \frac{1}{3}$

Xem đáp án

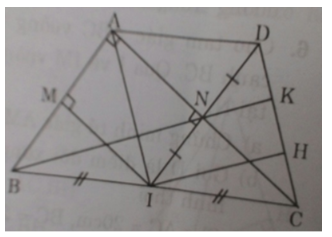
a) Xét tứ giác AMIN có:

∠(MAN) = ∠(ANI) = ∠(IMA) = 90o

⇒ Tứ giác AMIN là hình chữ nhật (có 3 góc vuông).

b) ΔABC vuông có AI là trung tuyến nên AI = IC = BC/2

do đó ΔAIC cân có đường cao IN đồng thời là đường trung tuyến

⇒ NA = NC.

Mặt khác ND = NI (t/c đối xứng) nên ADCI là hình bình hành

Lại có AC ⊥ ID (gt). Do đó ADCI là hình thoi.

c) Ta có: AB2 = BC2 – AC2 (định lí Py-ta-go)

= 252 – 202 ⇒ AB = √225 = 15 (cm)

Vậy SABC = (1/2).AB.AC = (1/2).15.20 = 150 (cm2)

d) Kẻ IH // BK ta có IH là đường trung bình của ΔBKC

⇒ H là trung điểm của CK hay KH = HC (1)

Xét ΔDIH có N là trung điểm của DI, NK // IH (BK // IH)

Do đó K là trung điểm của DH hay DK = KH (2)

Từ (1) và (2) ⇒ DK = KH = HC ⇒ DK/DC= 1/3.

Bắt đầu thi ngay