Giải toán bằng cách lập phương trình có đáp án
-
1103 lượt thi
-
25 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Gọi độ dài quãng đường AB là x (km), với x > 0
Vì hai xe gặp nhau ở địa điểm cách đều A và B nên quãng đường đi được của mỗi xe là (km).
Thời gian đi quãng đường AB của xe đi từ A là. (h)
Thời gian đi quãng đường AB của xe đi từ B là. (h)
Theo đề bài ta có phương trình:
Vậy quãng đường AB dài 1440 km.
Câu 2:
Một người đi xe đạp từ A đến B cách nhau km. Khi từ B trở về A người đó tăng vận tốc lên km/h so với lúc đi, vì vậy thời gian về ít hơn thời gian đi phút. Tính vận tốc của xe đạp khi đi từ A đến B.
 Xem đáp án
Xem đáp án
|
|
Vận tốc |
Thời gian |
Quãng đường |
|
Lúc đi |
x
|
|
24
|
|
Lúc về |
x + 4
|
|
24
|
Gọi vận tốc của xe đạp khi đi từ A đến B là x (km/h). Điều kiện: x > 0
Vận tốc khi từ B trở về A là x+4 (km/h).
Thời gian lúc đi và lúc về lần lượt là và (giờ).
Vì thời gian về ít hơn thời gian đi là phút giờ nên ta có phương trình :
x2 + 4x - 192 = 0
x+2 =
x = 12 (TM) ; x = -16 (L)
Vậy vận tốc lúc đi là 12 (km/h).
Câu 3:
Một người đi bộ từ A đến B với vận tốc dự định 4 km/h. Sau khi đi được nửa quãng đường AB với vận tốc đó, người ấy đi bằng ô tô với vận tốc 30 km/h, do đó đã đến B sớm hơn dự định 2 giờ 10 phút. Tính chiều dài quãng đường AB.
 Xem đáp án
Xem đáp án
Đổi 2 giờ 10 phút = giờ
Gọi chiều dài quãng đường AB là x (km), (x > 0)
Thời gian người đó đi nửa quãng đường AB với vận tốc 4 km/h là
(giờ)
Thời gian người đó đi quãng đường còn lại với vận tốc 30 km/h là
(giờ)
Theo đề bài, người đó đến B trước 2 giờ 10 phút ( giờ)nên ta có phương trình :
Giải phương trình, tìm được x = 20 (thỏa mãn điều kiện của ẩn)
Trả lời : Quãng đường AB dài 20 km
Câu 4:
Để đi đoạn đường từ A đến B, xe máy phải đi hết 3giờ 30’; ô tô đi hết 2giờ 30’ phút. Tính quãng đường AB. Biết vận tốc ôtô lớn hơn vận tốc xe máy là 20km/h.
 Xem đáp án
Xem đáp án
chọn x (km) là chiều dài đoạn đường AB; điều kiện: x > 0
Biểu thị các đại lượng chưa biết qua ẩn và qua các đại lượng đã biết.
Vận tốc xe máy : (km/h)
Vận tốc ôtô : (km/h)
Dựa vào các mối liên hệ giữa các đại lượng(v2 – v1 = 20)
- Giải phương trình trên ta được x = 175. Giá trị này của x phù hợp với điều kiện trên. Vậy ta trả lời ngay được chiều dài đoạn AB là 175km.
Sau khi giải xong, giáo viên cần cho học sinh thấy rằng : Như ta đã phân tích ở trên thì bài toán này còn có vận tốc của mỗi xe chưa biết, nên ngoài việc chọn quãng đường là ẩn, ta cũng có thể chọn vận tốc xe máy hoặc vận tốc ôtô là ẩn.
- Nếu gọi vận tốc xe máy là x (km/h) : x > 0
Thì vận tốc ôtô là x + 20 (km/h)
- Vì quãng đường AB không đổi nên có thể biểu diễn theo hai cách (quãng đường xe máy đi hoặc của ôtô đi).
- Ta có phương trình : 3,5 x = 2,5 (x + 20)
Giải phương trình trên ta được: x = 50.
Câu 5:
Một tàu tuần tra chạy ngược dòng 60km, sau đó chạy xuôi dòng 48 km trên cùng một dòng sông có vận tốc của dòng nước là 2km/h. Tính vận tốc của tàu tuần tra khi nước yên lặng, biết thời gian xuôi dòng ít hơn thời gian ngược dòng là 1 giờ.
 Xem đáp án
Xem đáp án
Gọi vận tốc của tàu khi nước yên lặng là x ( km/h). Điều kiện: x > 2.
Vận tốc lúc xuôi dòng và ngược dòng lần lượt là x + 2; x – 2 (km/h).
Thời gian khi xuôi dòng và ngược dòng lần lượt là và (giờ).
Vì thời gian xuôi dòng ít hơn thời gian ngược dòng 1 giờ nên ta có phương trình
x2 - 12x – 220 = 0 x2 - 12x + 36 – 256 = 0 (x – 6)2 = 256
x – 6 = x = 22 ( thỏa mãn), x = - 10 (loại)
Vậy vận tốc của tàu thủy khi nước yên lặng là 22 ( km/h).
Câu 6:
Trong tháng đầu hai tổ công nhân của một xí nghiệp dệt được 800 tấm thảm len. Tháng thứ hai tổ I vượt mức 15%, tổ 2 vượt mức 20% nên cả hai tổ dệt được 945 tấm thảm len. Tính xem trong tháng thứ hai mỗi tổ đã dệt được bao nhiêu tấm thảm len
 Xem đáp án
Xem đáp án
Gọi số tấm thảm len tổ I dệt được trong tháng đầu là x (x Î Z+, x < 800)
Trong tháng đầu cả hai tổ dệt được 800 tấm thảm len nên số tấm thảm len tổ II dệt được trong tháng đầu là (800 - x)
Tháng thứ hai tổ I dệt được (tấm thảm)
Tháng thứ hai tổ II dệt được (tấm thảm)
Theo đề bài trong tháng hai cả hai tổ dệt được 945 tấm thảm nên ta có phương trình :
Giải phương trình, tìm được x = 300 (thỏa mãn điều kiện)
Vậy : Trong tháng thứ hai tổ I dệt được (tấm thảm len), tổ II dệt được 300 (tấm thảm len)
Câu 7:
 Xem đáp án
Xem đáp án
Gọi số sản phẩm dự kiến làm trong mỗi ngày là x (sản phẩm).
Điều kiện: x > 0
Thời gian dự kiến là (ngày).
Thời gian làm 400 sản phẩm đầu là (ngày).
Thời gian làm 600 - 400 = 200 sản phẩm sau là (ngày).
Vì thực tế công việc hoàn thành sớm hơn dự kiến 1 ngày nên ta có phương trình:
x + 5 =
x = 40 ( thỏa mãn), x = -50 (loại).
Vậy số sản phẩm dự kiến làm trong mỗi ngày là 40 (sản phẩm).
Câu 8:
 Xem đáp án
Xem đáp án
Gọi số sản phẩm mỗi ngày người thợ đó cần làm theo dự định là x (sản phẩm).
Điều kiện: x > 2.
Số ngày theo dự định là (ngày).
Trong 50 sản phẩm đầu, mỗi ngày người thợ đó làm được x-2 (sản phẩm) nên số ngày làm 50 sản phẩm đầu là (ngày).
Trong 120-50=70 sản phẩm sau, mỗi ngày người thợ đó làm được x+2 (sản phẩm) nên số ngày làm 70 sản phẩm đầu là (ngày).
Do thực tế người đó hoàn thành đúng như dự định nên ta có phương trình:
( thỏa mãn điều kiện).
Vậy số sản phẩm mỗi ngày người thợ dó cần làm theo dự định là 12 (sản phẩm).
Câu 9:
Hai đội công nhân cùng sửa một con mương hết 24 ngày. Mỗi ngày phần việc làm được của đội 1 bằng 1 phần việc của đội 2 làm được. Nếu làm một mình, mỗi đội sẽ sửa xong con mương trong bao nhiêu ngày?
 Xem đáp án
Xem đáp án
Gọi số ngày một mình đội 2 phải làm để sửa xong con mương là x ( ngày)
Điều kiện x > 0 .
Trong một ngày đội 2 làm được công việc.
Trong một ngày đội 1 làm được (công việc ).
Trong một ngày cả hai đội làm được công việc.
Theo bài ra ta có phương trình:
24 + 36 = x
x = 60 thoả mãn điều kiện
Vậy, thời gian đội 2 làm một mình sửa xong con mương là 60 ngày.
Mỗi ngày đội 1 làm được công việc.
Để sửa xong con mương đội 1 làm một mình trong 40 ngày.
Câu 10:
Khối 8 một trường THCS có số lớp nhiều hơn 2, tổ chức trồng cây:
Lớp thứ nhất trồng 5 cây và số cây còn lại.
Lớp thứ hai trồng tiếp 10 cây và số cây còn lại.
Lớp thứ ba trồng tiếp 15 cây và số cây còn lại.
Cử trồng như vậy đến lớp cuối cùng thì vừa hết số cây và số cây mỗi lớp trồng được là bằng nhau. Tính số cây mà khối 8 trồng và số lớp 8 của khối tham gia trồng cây.
 Xem đáp án
Xem đáp án
Mỗi lớp trồng: (cây)
Số lớp 8 tham gia trồng cây: 80: 20 = 4 (lớp)
Câu 11:
Trong tháng giêng cả hai tổ công nhân cùng sản xuất được 800 chi tiết máy. Sang tháng hai tổ I vượt mức 15%, tổ II vượt mức 20%, do đó cả hai tổ đã sản xuất được 945 chi tiết máy. Tính xem trong tháng giêng mỗi tổ đã sản xuất được bao nhiêu chi tiết máy?
 Xem đáp án
Xem đáp án
Gọi x là số chi tiết máy tổ I đã làm trong tháng giêng ( nguyên dương ) thì số chi tiết máy mà tổ II làm trong tháng giêng là ( 800 – x ). Sang tháng hai, tổ I, tổ II lần lượt làm được và chi tiết máy.
Theo đề bài ta có phương trình:
Giải ra, ta được x=300 thỏa mãn điều kiện đề bài.
Vậy trong tháng giêng tổ I làm được 300 chi tiết máy và tổ II làm được 500 chi tiết máy.
Câu 12:
Lan có một miếng bìa hình tam giác ABC vuông tại A, cạnh AB = 3cm. Lan tính rằng nếu cắt từ miếng bìa đó ra một hình chữ nhật có chiều dài 2cm như hình bên thì hình chữ nhật ấy có diện tích bằng một nửa diện tích của miếng bìa ban đầu. Tính độ dài cạnh AC của tam giác ABC
 Xem đáp án
Xem đáp án
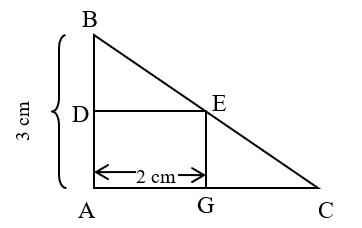
Gọi x là độ dài cạnh AC (x Î Z+, cm)
Diện tích tam giác ABC là 3x (cm2)
Diện tích hình chữ nhật ADEG là cm2 và chiều rộng hình chữ nhật là : cm.
Diện tích hình chữ nhật bằng tổng diện tích hai tam giác BDE và CEG và ta có phương trình :
SADGE = SBDE + SCEG
Û
Û x = 4
Vậy : Cạnh AC của tam giác ABC có độ dài 4cm.
Câu 13:
Một hình chữ nhật có chu vi bằng 320m. nếu tăng chiều dài thêm 10m và tăng chiều rộng thêm 20m thì diện tích hình chữ nhật tăng thêm 2700m2. Tính kích thước của hình chữ nhật.
 Xem đáp án
Xem đáp án
Gọi chiều dài của hình chữ nhật là x (đơn vị : m).
Điều kiện của ẩn là 0 < x < 160
Khi đó chiều rộng hình chữ nhật là 160 - x (m).
Diện tích hình chữ nhật ban đầu là x (160-x) ( m2).
Sau khi tăng chiều dài thêm 10m, chiều rộng thêm 20m thì chiều dài mới là: x + 10
và chiều rộng mới là: 180 - x
Khi đó diện tích hình chữ nhật là (x+10) (180-x)
Theo bài ra, diện tích hình chữ nhật tăng 2700 m2, nên ta có phương trình:
Hay 10x = 900
Tức là x = 90 (m).
Ta thấy giá trị thỏa mãn điều kiện đặt ra.
Vậy chiều dài của hình chữ là 90m, chiều rộng của nó là 70m.
Câu 14:
Bà An gửi vào quỹ tiết kiệm x nghìn đồng với lãi suất mỗi tháng là a% (a là một số cho trước) và lãi tháng này được tính gộp vào vống cho tháng sau.
a. Hãy viết biểu thức biểu thị :
+ Số tiền lãi sau tháng thứ nhất;
+ Số tiền (cả gốc lẫn lãi) có được sau tháng thứ nhất;
+ Tổng số tiền lãi có được sau tháng thứ hai.
 Xem đáp án
Xem đáp án
Số tiền lãi sau một tháng gửi với lãi suất a% với tiền gửi x nghìn đồng là ax. Số tiền có được (cả gốc lẫn lãi) sau tháng thứ nhất : x + ax = x (1 + a) nghìn đồng.
Số tiền lại sau hai tháng là : L = ax + ax(1+a) = x(a2 + 2a)
Câu 15:
Nếu lãi suất là 1,2% (tức là a = 1,2) và sau 2 tháng tổng số tiền lãi là 48,288 nghìn đồng, thì lúc đầu bà An đã gửi bao nhiêu tiền tiết kiệm?
 Xem đáp án
Xem đáp án
Thay a = 1,2% là L = 48,288 ta được :
x () = 48,288 nghìn đồng
Þ x = 2000000 đồng
Câu 16:
 Xem đáp án
Xem đáp án
Gọi số người của đội II lúc đầu là x. ĐK : x nguyên dương
Số người của đội I lúc đầu là 2x.
Sau khi chuyển 10 người từ đội I sang đội II thì số người còn lại của đội I là 2x - 10 (người), số người của đội II là x + 10 (người).
Theo đề bài khi đó số người ở đội II bằng số người của đội I nên ta có phương trình :
x + 10 = (2x - 10)
Giải phương trình, tìm được x = 30 (thỏa mãn điều kiện)
Câu 17:
Học kì I số học sinh của lớp 8A bằng số học sinh của cả lớp. Sang học kì II có ba bạn phấn đấu trở thành học sinh giỏi nữa. Do đó số học sinh giỏi bằng 20% số học sinh của cả lớp. Hỏi lớp 8A có bao nhiêu học sinh giỏi.
 Xem đáp án
Xem đáp án
Ta lập phương trình như sau:
Gọi số học sinh của lớp là x (điều kiện nguyên dương), thì số học sinh giởi của học kì I so với số học sinh của cả lớp bằng , số học sinh giỏi của học kì II so với số học sinh của cả lớp bằng 20% số học sinh của cả lớp hay bằng và số học sinh giỏi học kì II hơn số học sinh giỏi học kì I là 3 em nên ta có phương trình:
Giải phương trình này ta tìm được x = 40. Giá trị này thỏa mãn điều kiện đặt ra nên là nghiệm của phương trình.
Vậy số học sinh của lớp 8A là 40 em.
Câu 18:
“Một số tự nhiên có hai chữ số, tổng các chữ số của nó là 16, nếu đổi chỗ hai chữ số cho nhau được một số lớn hơn số đã cho là 18 đơn vị. Tìm số đã cho.
 Xem đáp án
Xem đáp án
Nếu gọi chữ số hàng chục là x
Điều kiện của x ? (x N, 0 < x < 10).
Chữ số hàng đơn vị là : 16 – x
Số đã cho được viết 10x + 16 - x = 9x + 16
Đổi vị trí hai chữ số cho nhau thì số mới được viết :
10 ( 16 – x ) + x = 160 – 9x
Số mới lớn hơn số đã cho là 18 nên ta có phương trình :
(160 – 9x) – (9x + 16) = 18
- Giải phương trình ta được x = 7 (thỏa mãn điều kiện).
Vậy chữ số hàng chục là 7.
Chữ số hàng đơn vị là 16 – 7 = 9.
Số cần tìm là 79.
Câu 19:
Tìm số tự nhiên có chữ số tận cùng là 5. Biết rằng nếu xóa chữ tận cùng này thì được một số mới nhỏ hơn số đầu là 2003 đơn vị.
 Xem đáp án
Xem đáp án
Gọi số cần tìm là Theo đề bài ta có:
= x +2003
Suy ra x = 2225
Vậy số cần tìm là 2225.
Câu 20:
Cho phân số . Hãy tìm số tự nhiên m sao cho khi đem cả tử số và mẫu số trừ đi m thì được phân số mới bằng .
 Xem đáp án
Xem đáp án
Gọi m là số phải tìm. Theo đề bài ta có:
Suy ra m = 29
Vậy số m phải tìm là 29.
Câu 21:
Biết rằng 200g một dung dịch chứa 50g muối. Hỏi phải pha thêm bao nhiêu gam nước vào dung dịch đó để được một dung dịch chứa 20% muối?
 Xem đáp án
Xem đáp án
Gọi x là lượng nước cần pha thêm vào dung dịch đã cho (x > 0, g)
Khi đó lượng dung dịch nước là 200 + x.
Nồng độ dung dịch là
Theo đề bài ta có phương trình :
Û 20(150 + x) = 5000
Û x = 100
Vậy : Lượng nước cần pha thêm là 100 g
Câu 22:
Có hai loại thép vụn chứa 5% và 40% nicken. Cần lấy bao nhiêu thép vụn mỗi loại để luyện được 140 tấn thép chứa 30% nicken?
 Xem đáp án
Xem đáp án
Gọi khối lượng thép vụn loại 5% nicken cần lấy là (đơn vị tấn, điều kiện > 0 ). Khối lượng nicken có trong loại thép vụn này là: (tấn)
Khối lượng thép vụn loại 40% nicken cần lấy là: 140 - x(tấn).
Khối lượng nicken có trong loại thép vụn này là (tấn)
Khối lượng nicken chức trong 140 tấn thép là: 42 ( tấn ).
Theo bài ra ta có phương trình: Suy ra x = 40
Vậy loại thép vụn 5% nicken cần lấy là 40 tấn, loại 40% cần lấy là 100 tấn.
Câu 23:
Quãng đường AD gồm ba đoạn AB; BC và CD. Lúc 7 giờ sáng một người đi ô tô từ A với vận tốc 60km/h đến B lúc 7giờ 30phút, sau đó đi tiếp trên đoạn đường BC vận tốc 50km/h. Cùng lúc 7 giờ sáng một người đi xe máy đi từ C với vận tốc 35km/h để đến D. Biết thời gian người đi xe máy đến D nhiều hơn thời gian người đi ô tô từ B đến c là 1 giờ 24 phút và quãng đường BC ngắn hơn quãng đường CD là 40km. Tính quãng đường AD.
 Xem đáp án
Xem đáp án
Thời gian xe đi hết quãng đường AB là 7 giờ 30 phút - 7 giờ = 30 phút = 0,5 h. Ta có quãng đường AB dài là 60. 0,5 = 30(km).
Gọi quãng đường BD là x(km); x > 40. Do đoạn CD dài hơn BC là 40km; tổng hai đoạn đường là x (km) nên:
- Đoạn đường BC dài (km); đoạn đường CD dài (km)
- Thời gian ô tô đi trên đoạn BC là (h).
- Thời gian ô tô đi trên đoạn CD là (h).
1 giờ 24 phút = 1,4 giờ
Theo bài ra ta có phương trình:
- Giải phương trình: x = 100
Giá trị này phù hợp với điều kiện của ấn vậy:
Quãng đường BD dài 100 km và quãng đường AD dài 100 + 30 = 130 (km).
Câu 24:
Trên quãng sông AB dài 48km, một ca nô xuôi từ A đến B rồi quay trở lại và đỗ tại một địa điểm C ở chính giũa A và B. Thời gian ca nô cả xuôi và ngược dòng hết tất cả 3 giờ 30 phút. Tính vận tốc riông của ca nô biết rằng một bè nứa thả trôi trên sông đó 15 phút trôi được 1 km.
 Xem đáp án
Xem đáp án
15 phút = 0,25 giờ; 3 giờ 30 phút = 3,5 giờ.
Vận tốc bè nứa trôi là 1: 0,25 = 4 (km/h) chính là vận tốc dòng nước.
Gọi vận tốc riêng của ca nô là x (km/h); x > 4. Thì vận tốc ca nô khi xuôi dòng là x + 4 (km/h), vận tốc ca nô khi ngược dòng là x - 4 (km/h).
Thời gian ca nô xuôi dòng là (h) và ngược dòng là (h).
Theo bài ra ta có phương trình: 48x - 192 + 24x + 96 = 3,5 x2 -56
Trong hai giá trị trên x = 20 thỏa mãn điều kiện đầu bài.
Vậy vận tốc riêng của ca nô là 20km/h.
Câu 25:
Hai xưởng sản xuất cùng làm một sản phẩm, số sản phẩm xưởng thứ nhất làm trong 5 ngày nhiều hơn số sản phẩm xưởng thứ hai làm trong 6 ngày là 140 sản phẩm. Biết rằng năng suất lao động của xưởng thứ nhất hơn xưởng thứ hai là 65 sản phẩm/ngày. Tính năng suất lao động của mỗi xưởng.
 Xem đáp án
Xem đáp án
Năng suất lao động của xưởng thứ hai là 250 - 65 = 185 (sản phẩm /ngày).
