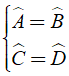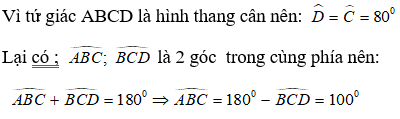9 câu hỏi trắc nghiệm thuộc Bài tập Hình thang cân (có lời giải chi tiết)

Bài tập Hình thang cân (có lời giải chi tiết)

Đề số 1

Bài tập Hình thang cân (có lời giải chi tiết)

1584 lượt thi
9 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Điền cụm từ thích hợp vào chỗ trống

A. Hình thang cân là…………………………………..

B. Hình thang có………………. là hình thang cân .

C. Hai cạnh bên của hình thang cân…………………..

D. Hình thang cân có hai góc kề một đáy…………….

Xem đáp án

+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

→ Đáp án A điền: “hình thang có hai góc kề một đáy bằng nhau”.

+ Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.

→ Đáp án B điền: “hai góc kề một đáy bằng nhau”

+ Hai cạnh bên của hình thang cân bằng nhau.

→ Đáp án C điền: “bằng nhau”

+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau

→ Đáp án D điền: “bằng nhau”

Câu 2:

Điền chữ “Đ” hoặc “S” vào mỗi câu khẳng định sau:

A. Tứ giác có hai cạnh bên bằng nhau là hình thang cân.

B. Hình thang cân có hai cạnh bên bằng nhau.

C. Hình thang cân có hai góc kề một cạnh đáy bù nhau.

D. Hình thang cân có hai góc kề một cạnh đáy bằng nhau.

Xem đáp án

+ Tứ giác có hai cạnh bên bằng nhau là hình thang cân.

→ Đáp án A sai vì hai cạnh bên bằng nhau chưa chắc tạo ra hình thang.

+ Hình thang cân có hai cạnh bên bằng nhau.

→ Đáp án B đúng.

+ Hình thang cân có hai góc kề một cạnh đáy bằng nhau.

→ Đáp án D đúng, đáp án C sai.

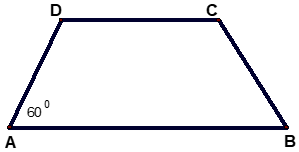
Câu 3:

Cho hình thang cân ABCD (như hình vẽ) có $\hat{B A D} = 60^{0}$ . Số đo của $\hat{B C D} = ?$

A. $50^{0}$

B. $60^{0}$

C. $120^{0}$

D. $80^{0}$

Xem đáp án

Áp dụng tính chất của hình thang cân ta có:

Câu 4:

Cho hình thang cân ABCD (AB//CD), gọi E là giao điểm của AC và BD. Tìm mệnh đề sai ?

A. $∆ A B C = ∆ B A D$

B. $\hat{C A B} = \hat{D B A}$

C. tam giác ABE cân

D. tam giác AED cân

Xem đáp án

Chọn D

Câu 5:

Cho hình thang cân ABCD (AB// CD) và $\hat{D} = 80^{o}$ . Tính $\hat{A B C}$

A. $100^{o}$

B. $90^{o}$

C. $80^{o}$

D. $110^{o}$

Xem đáp án

Chọn A

Câu 6:

Cho hình thang ABCD có AB // CD , hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD . Tìm khẳng định sai trong các khẳng định sau?

A. ABCD là hình thang cân

B. AC = BD

C. BC = AD

D. Tam giác AOD cân tại O.

Xem đáp án

* Ta có: OA = OB nên tam giác OAB cân tại O

* Do OC = OD nên tam giác OCD cân tại O

* vì OA = OB và OC = OD nên OA + OC = OB + OD

Hay AC = BD

Hình thang ABCD có hai đường chéo AC = BD nên đây là hình thang cân.

Suy ra: BC = AD và $\hat{B A D} = \hat{A B C}; \hat{A D C} = \hat{D C B}$

Chọn đáp án D

Câu 7:

Cho hình thang cân ABCD có AB // CD và $\hat{A} = 125^{o}$ . Tính $\hat{B}$ ?

A. $125^{o}$

B. $65^{o}$

C. $90^{o}$

D. $55^{o}$

Xem đáp án

Câu 8:

Cho hình thang cân ABCD có AB// CD và AB = BC. Tìm khẳng định sai.

A. $\hat{B A C} = \hat{A C B}$

B. $\hat{A D B} = \hat{A B D}$

C. tam giác ABD cân tại A

D. $\hat{B D C} = \hat{A C B}$

Xem đáp án

* Xét tam giác ABC có AB = BC nên tam giác ABC cân tại B.

Suy ra: $\hat{B A C} = \hat{A C B}$

* Vì ABCD là hình thang cân nên AD = BC

Lại có AB = BC nên AB = AD.

* Suy ra: ΔABD cân tại A nên $\hat{A D B} = \hat{A B D}$

Chọn đáp án D

Câu 9:

Cho hình thang cân ABCD có AB // CD. Gọi giao điểm của AD và BC là M . Tam giác MCD là tam giác gì ?

A. Tam giác cân

B. Tam giác nhọn

C. Tam giác vuông

D. Tam giác tù

Xem đáp án

Bắt đầu thi ngay