15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 8 CTST Bài 2. Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều có đáp án

Câu 1:

Diện tích xung quanh của hình chóp tứ giác đều được tính bằng?

A. tổng diện tích tất cả các mặt.

B. tổng diện tích các mặt bên.

C. diện tích mặt đáy.

D. tổng diện tích một mặt bên và mặt đáy.

Xem đáp án

Lời giải

Đáp án đúng là: B

Diện tích xung quanh của hình chóp tứ giác đều bằng tổng diện tích các mặt bên.

Câu 2:

Cho hình chóp tứ giác đều, thể tích của hình chóp được tính bằng:

A. \(\frac{1}{3}\) tích của diện tích mặt đáy với chiều cao.

B. \(\frac{1}{3}\) tích của diện tích mặt đáy với trung đoạn.

C. tích của diện tích mặt đáy với chiều cao.

D. tích của diện tích mặt đáy với trung đoạn.

Xem đáp án

Lời giải

Đáp án đúng là: A

Thể tích của hình chóp tứ giác đều bằng \(\frac{1}{3}\) tích của diện tích đáy với chiều cao của nó.

Câu 3:

Tính diện tích xung quanh của hình chóp tứ giác đều biết chiều cao một mặt bên của hình chóp bằng 5 cm, cạnh đáy của hình chóp bằng 4 cm.

A. 20 cm²

B. 60 cm²

C. 40 cm²

D. 80 cm²

Xem đáp án

Lời giải

Đáp án đúng là: C

Diện tích xung quanh của hình chóp tứ giác đều bằng tổng diện tích các mặt bên.

Mà hình chóp tứ giác đều có 4 mặt bên nên

\[{S_{xq}} = S\,.\,4 = \left( {\frac{1}{2}.\,5\,.\,4} \right)\,.\,4 = 40\,\,\left( {c{m^2}} \right)\].

Câu 4:

Cho hình chóp tam giác đều có diện tích một mặt bên là 50cm².Tính diện tích xung quanh của hình chóp đó.

A. 50 cm²

B. \(\frac{{100}}{3}\,\,c{m^2}\)

C. 150 cm²

D. 100 cm²

Xem đáp án

Lời giải

Đáp án đúng là: C

Theo công thức tính diện tích xung quanh của hình chóp tam giác đều nên:

\[{S_{xq}} = 50\,.\,3 = 150\,\,\left( {c{m^2}} \right)\]

Câu 5:

Cho hình chóp tam giác đều có thể tích bằng 250 cm², chiều cao hình chóp bằng 30 cm. Tính diện tích mặt đáy của hình chóp đó.

A. 7 500 cm²

B. 25 cm²

C. 250 cm²

D. \(\frac{{25}}{3}\) cm²

Xem đáp án

Lời giải

Đáp án đúng là: B

Theo công thức tính thể tích của hình chóp tam giác đều: \[V = \frac{1}{3}.\,S\,.\,h\]

Suy ra \[S = \frac{{3V}}{h} = \frac{{3\,.\,250}}{{30}} = 25\,\,\left( {c{m^2}} \right)\]

Câu 6:

Cho hình chóp tứ giác đều có cạnh đáy bằng 4 cm, chiều cao của hình chóp bằng 9 cm. Tính thể tích của hình chóp đó.

A. 48 cm³

B. 144 cm³

C. 72 cm³

D. 36 cm³

Xem đáp án

Lời giải

Đáp án đúng là: A

Theo công thức thể tích của hình chóp tam giác đều nên:

\[V = \frac{1}{3}.\,S\,.\,h = \frac{1}{3}.\,\left( {4\,.\,4} \right)\,.\,9 = 48\,\,\left( {c{m^3}} \right)\]

Câu 7:

Cho hình chóp tam giác đều S.ABC có các mặt bên là các tam giác đều diện tích 10 cm², diện tích mặt đáy là 20 cm². Tính diện tích toàn phần của hình chóp đó.

A. 50 cm²

B. 20 cm²

C. 40 cm²

D. 30 cm²

Xem đáp án

Lời giải

Đáp án đúng là: A

Diện tích toàn phần của hình chóp tam giác đều bằng tổng diện tích xung quanh và diện tích đáy.

Vậy diện tích toàn phần của hình chóp S.ABC là

\[{S_{tp}} = {S_{xq}} + {S_{day}} = 3\,.10 + 20 = 50\,\,\left( {c{m^2}} \right)\]

Câu 8:

Tính diện tích bìa cần để làm một hộp quà hình chóp tam giác đều có bốn mặt là tam giác đều bằng nhau cạnh 4,4 cm và chiều cao mặt đáy bằng 3 cm (không tính mép dán).

A. 24,6 cm²

B. 20 cm²

C. 40 cm²

D. 26,4 cm²

Xem đáp án

Lời giải

Đáp án đúng là: D

Vì tất cả các mặt đều là tam giác đều bằng nhau nên diện tích của các mặt đều bằng nhau.

Khi đó diện tích bìa cần dùng là

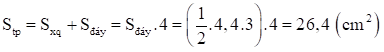
Media VietJack

Câu 9:

Một chiếc bánh hình chóp tam giác đều có chiều cao của hình chóp là 9 cm, tam giác đáy có cạnh đáy bằng 4 cm , chiều cao bằng \(2\sqrt 2 \,\,c{m^2}\). Tính thể tích của chiếc bánh đó.

A. 12 cm³

B. 24 cm³

C. \(12\sqrt 2 \,\,c{m^3}\)

D. \(24\sqrt 2 \,\,c{m^3}\)

Xem đáp án

Lời giải

Đáp án đúng là: C

Theo công thức thể tích của hình chóp tam giác đều, thể tích chiếc bánh là:

\[V = \frac{1}{3}.\,S\,.\,h = \frac{1}{3}.\left( {\frac{1}{2}.\,4\,.\,2\sqrt 2 } \right).\,9 = 12\sqrt 2 \,\,\left( {c{m^3}} \right)\]

Câu 10:

Cho khối chóp tứ giác đều, nếu tăng cạnh đáy lên ba lần và giảm chiều cao đi ba lần thì thể tích của khối chóp thay đổi như thế nào?

A. Giảm đi 9 lần.

B. Tăng lên 3 lần.

C. Giảm đi 3 lần.

D. Tăng lên 9 lần.

Xem đáp án

Lời giải

Đáp án đúng là: B

Nếu cạnh đáy tăng lên 3 lần thì diện tích đáy tăng 9 lần. Vì chiều cao giảm đi 3 lần nên thể tích khối chóp tăng lên 3 lần.

Câu 11:

Cho hình chóp tam giác đều có thể tích là 250 cm², diện tích đáy bằng 50 cm². Tính chiều cao của hình chóp đó.

A. 15 cm

B. 5 cm

C. 10 cm

D. 25 cm

Xem đáp án

Lời giải

Đáp án đúng là: A

Theo công thức tính thể tích của hình chóp tam giác đều: \[V = \frac{1}{3}.\,S\,.\,h\]

Suy ra \[h = \frac{{3V}}{S} = \frac{{3\,.\,250}}{{50}} = 15\,\,(cm)\]

Câu 12:

Một hình chóp tứ giác đều có thể tích bằng 50 cm³, chiều cao hình chóp bằng 6 cm, chiều cao mặt bên bằng 4cm. Tính diện tích xung quanh hình chóp đó.

A. 40 cm²

B. 50 cm²

C. 60 cm²

D. 80 cm²

Xem đáp án

Lời giải

Đáp án đúng là: A

Diện tích đáy của hình chóp là :\[50\,.\,3:6 = 25\,\,\left( {c{m^2}} \right)\]

Gọi x là độ dài cạnh đáy, vì đáy hình chóp tứ giác đều là hình vuông nên ta có \[{{\rm{x}}^{\rm{2}}}{\rm{ = 25}} \Rightarrow {\rm{x = 5}}\,\,{\rm{cm}}\].

Diện tích một mặt bên là: \[S = \frac{1}{2}.\,5\,.\,4 = 10\,\,(c{m^2})\]

Diện tích xung quanh của hình chóp trên là: \[{S_{xq}} = 4S = 4.10 = 40\,\,(c{m^2})\]

Câu 13:

Cho hình chóp tứ giác đều S. ABCD có diện tích xung quanh bằng 72 cm², chiều cao có độ dài bằng 6 cm, chiều cao một mặt bên là 4 cm. Thể tích của khối chóp đó là

A. 36 cm³

B. 162 cm³

C. \(162\sqrt 3 \,\,c{m^3}\)

D. 72 cm³

Xem đáp án

Lời giải

Đáp án đúng là: B

Diện tích một mặt bên là: \[72:4 = 18\,\,({\rm{c}}{{\rm{m}}^{\rm{2}}})\]

Độ dài cạnh đáy là: \[18\,.\,2:4 = 9\,\,(cm)\]

Diện tích mặt đáy là: \[{S_{ABCD}} = 9\,.\,9 = 81\,\,\,\left( {c{m^2}} \right)\]

Áp dụng công thức thể tích khối chóp ta được: \[V = \frac{1}{3}.\,81\,.\,6 = 162\,\,\left( {c{m^3}} \right)\]

Câu 14:

Một cái bể hình hộp chữ nhật đựng nước, có chiều dài 1,2 m; chiều rộng 0,9m, chiều cao 1m. Hiện tại mực nước trong bể cao 0,5 m. Người ta dùng một chiếc gàu hình chóp tam giác đều diện tích đáy 180 cm², chiều cao 20 cm để múc nước vào bể. Cần múc bao nhiêu lần để đầy nước trong bể? (mỗi lần múc đầy gàu)

A. 25 lần.

B. 15 lần.

C. 45 lần.

D. 30 lần.

Xem đáp án

Lời giải

Đáp án đúng là: C

Thể tích nước cần để đổ vào bể là:

\({V_{n{\rm{uo}}c}} = 1,2\,.\,0,9.\left( {1 - 0,5} \right) = 0,54\,\,({m^3}) = 540\)(lít)

Thể tích gầu nước là:

\[{{\rm{V}}_{g\`a u}}{\rm{ = }}\frac{{\rm{1}}}{{\rm{3}}}{\rm{.180}}\,{\rm{.}}\,{\rm{20 = 1200}}\,\,{\rm{(c}}{{\rm{m}}^{\rm{3}}}{\rm{) = 12}}\] (lít).

Số lần cần múc để hết nước trong bể là: \[540:12 = 45\] (lần).

Câu 15:

Người ta làm một bugalow dạng hình chóp tứ giác đều có chiều cao 4 m, cạnh sàn nhà bằng 6 m. Người ta chia đôi làm hai tầng bằng một mặt phẳng song song với sàn, cách đỉnh của hình chóp một khoảng bằng nửa chiều cao, cạnh mặt sàn tầng hai bằng một nửa cạnh mặt sàn tầng một. Biết một người cần 3 m³ không khí, tính số người tối đa ở tầng dưới (hình vẽ bên dưới).

A. 16 người.

B. 20 người.

C. 18 người.

D. 14 người.

Xem đáp án

Lời giải

Đáp án đúng là: D

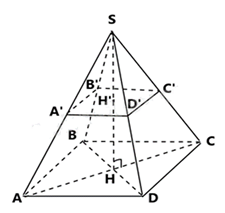
\[SH = 4\,\,m\] là chiều cao của bugalow

\[ \Rightarrow SH' = \frac{{SH}}{2} = 2\,\,(m)\]

\[A'B' = \frac{1}{2}AB = \frac{1}{2}.\,6 = 3\,\,(m)\]

Ta có:

\[{S_{A'B'C'D'}} = 3\,.\,3 = 9\,\,\left( {{m^2}} \right)\]

\[{{\rm{S}}_{{\rm{ABCD}}}}{\rm{ = 6}}{\rm{.6 = 36}}{{\rm{m}}^{\rm{2}}}\]

\[{V_{S.A'B'C'D'}} = \frac{1}{3}.{S_{A'B'C'D'}}\,.\,SH' = \frac{1}{3}.\,9\,.\,2{\rm{ }} = 6\,\,\left( {{m^3}} \right)\]

\[{V_{S.ABCD}} = \frac{1}{3}.\,{S_{ABCD}}\,.\,SH = \frac{1}{3}.\,36\,.\,4 = 48\,\,\left( {{m^3}} \right)\]

Thể tích phần không gian còn lại ở tầng dưới là:

\[{\rm{V = }}{{\rm{V}}_{{\rm{S}}{\rm{.ABCD}}}} - {{\rm{V}}_{{\rm{S}}{\rm{.A'B'C'D'}}}}{\rm{ = 48}} - 6 = 42\,\,\left( {{m^3}} \right)\]