Trắc nghiệm chuyên đề Toán 8 Chủ đề 8: Đối xứng tâm có đáp án
-
1010 lượt thi
-
8 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua A, F là điểm đối xứng với D qua C. Chứng minh:
a, AC // EF
Xem đáp án
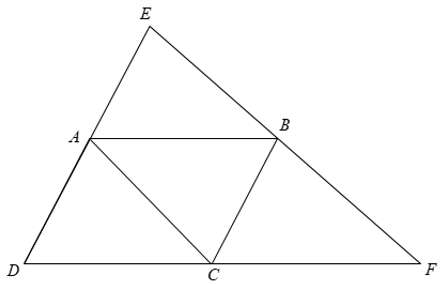
E là điểm đối xứng với D qua A ⇒ A là trung điểm của DE.
F là điểm đối xứng với D qua C ⇒ C là trung điểm của DF.
a) Xét Δ DEF có
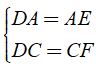
⇒ AC là đường trung bình của Δ DEF.
⇒ AC // EF
Câu 2:
b, Điểm E đối xứng với điểm F qua điểm B.
Xem đáp án
b) AC là đường trung bình của tam giác Δ DEF
⇒ AC = EF
+ ABCD là hình bình hành
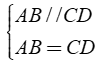
Mà DC = CF ⇒ AB = DF.
⇒ AB là đường trung bình của Δ DEF
Do đó B là trung điểm của EF hay E đối xứng với F qua B.
Câu 3:
Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, F là điểm đối xứng với D qua C. Chứng minh rằng E đối xứng với F qua B.
Xem đáp án
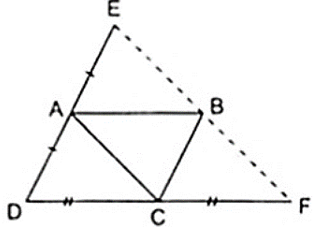
Theo giả thiết ta có:
+ A là trung điểm của DE thì AD = AE ( 1 )
+ C là trung điểm của DF thì CD = CF ( 2 )
Ta có ABCD là hình bình hành nên AD//BC
⇒ AE//BC ( 3 ) và AD = BC ( 4 )
Từ ( 1 ), ( 4 ) ⇒ AE = BC ( 5 )
Từ ( 3 ) và ( 5 ), tứ giác ACBE có cặp cạnh đối song song và bằng nhau nên là hình bình hành.
Áp dụng tính chất và định nghĩa về hình bình hành ACBE ta được
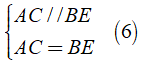
Chứng minh tương tự, tứ giác ACBF là hình bình hành
Ta được:
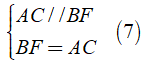
Từ ( 6 ), ( 7 ) ⇒ E, B, F thẳng hàng và BE = BF do đó B là trung điểm của EF hay E đối xứng với F qua B.
Câu 4:
Cho góc vuông xOy, điểm A nằm trong góc đó. Gọi B là điểm đối xứng với A qua Ox, C là điểm đối xứng với A qua Oy. Chứng minh B đối xứng với C qua O.
Xem đáp án
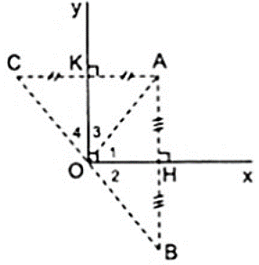
Vẽ AH ⊥ Ox, AK ⊥ Oy
Vẽ hai điểm B, C sao cho H, K lần lượt là trung điểm của AB, AC thì B là điểm đối xứng với A qua Ox, C là điểm đối xứng với A qua Oy.
Vì O ∈ Ox, O ∈ Oy nên O đối xứng với O qua Ox, Oy.
Áp dụng tính chất của phép đối xứng ta được
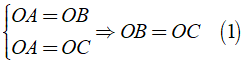
Và
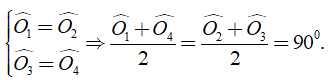
⇒ = {1800 } (2)
Từ ( 1 ), ( 2 ) suy ra O là trung điểm của BC hay B đối xứng với C qua O.
Câu 5:
Xem đáp án
Định nghĩa: Hai điểm gọi là đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.
Câu 6:
Xem đáp án
Định nghĩa: Hai điểm gọi là đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.
Khi đó, A' là điểm đối xứng với A qua B thì AB = BA' = 6cm
⇒ AA' = AB + BA' = 6 + 6 = 12cm
Câu 7:
Xem đáp án
Các hình có tâm đối xứng là giao điểm điểm của hai đường chéo là
+ Hình bình hành
+ Hình chữ nhật
+ Hình thoi
→ Hình thang không có tâm đối xứng là giao điểm của hai đường chéo.
Câu 8:
Xem đáp án
Ta có tính chất: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một điểm thì chúng bằng nhau.
Khi đó ta có:
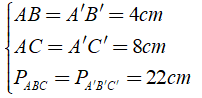
⇒ BC = B'C' = 22 - 8 - 4 = 10( cm )