Trắc nghiệm chuyên đề Toán 8 Chủ đề 7: Đề kiểm tra 45 phút_ đề số 1 có đáp án
-
1211 lượt thi
-
7 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho hình hộp chữ nhật ABCD.EFGH. Số các cặp mặt phẳng song song với nhau là:
Xem đáp án
Đáp án B
Câu 2:
Cho hình hộp chữ nhật ABCD.MNPQ có chiều dài AB = 22cm; chiều rộng BC = 14cm; chiều cao AM = 5cm. Thể tích hình hộp chữ nhật ABCD.MNPQ là:
Xem đáp án
Đáp án A
Câu 3:
Diện tích toàn phần của một hình lập phương là 726cm2. Thể tích của hình lập phương này là:
Xem đáp án
Đáp án C
Câu 5:
Một hình chóp tứ giác đều có thể tích bằng 96cm3, chiều cao của hình chóp là 8cm. Độ dài cạnh đáy của hình chóp bằng:
Xem đáp án
Đáp án A
Câu 6:
Cho hình hộp chữ nhật ABCD.EFGH. Chứng tỏ rằng:
a) ACGE là hình chữ nhật
b) DF = CE
Xem đáp án
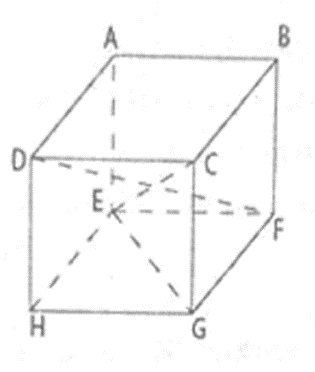
a) Ta có AE // CG; AE = CG (gt)
Tứ giác ACGE là hình bình hành
Mặt khác AE ⊥ mp(EFGH)
Mà EG ⊂ mp(EFGH) => AE ⊥ EG tại E
Vậy tứ giác ACGE là hình chữ nhật
b) Chứng minh DF = CE
Vì DH ⊥ mp(EFGH ) nên DH ⊥ HF tại H
Suy ra DF2 = DH2 + HF2(Py-ta-go) (1)
Vì AE ⊥ mp(ABCD) nên AE ⊥ AC tại A
Suy ra CE2 = AE2 + AC2(Py-ta-go) (2)
Mà DH = AE; HF = EG = AC (hai đường chéo của hình chữ nhật) (3)
Từ (1), (2) và (3) suy ra DF2 = CE2 => DF = CE
Câu 7:
Cho hình chóp tứ giác đều S.ABCD, đáy ABCD là hình vuông có cạnh 3cm, cạnh bên SA = 5cm.
a) Tính đường cao SH của hình chóp.
b) Tính diện tích xung quanh và thể tích của hình chóp.
Xem đáp án
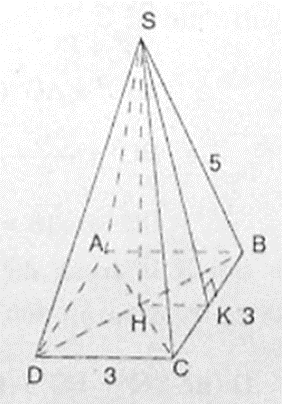
a) Ta có: AC2 = AB2 + BC2 (Pytago) = 32 + 32 = 18(cm)
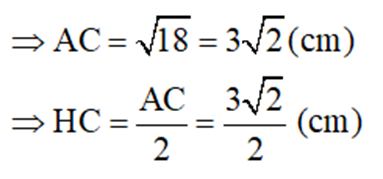
Lại có: SH2 = SC2 - HC2 (Pytago)
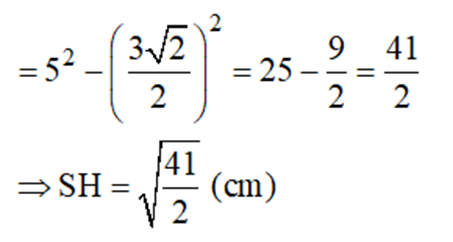
b) Gọi K là trung điểm của BC
Ta có: SK2 = SH2 + HK2 (Pytago)
