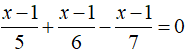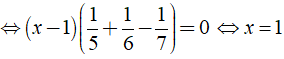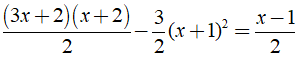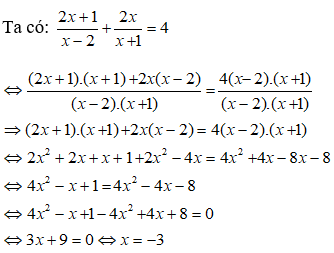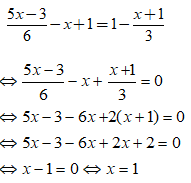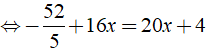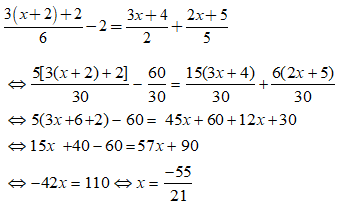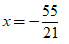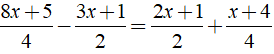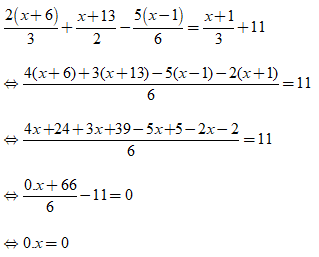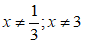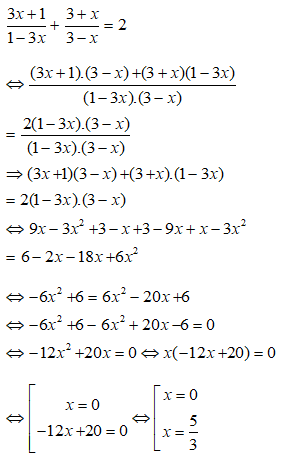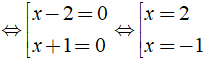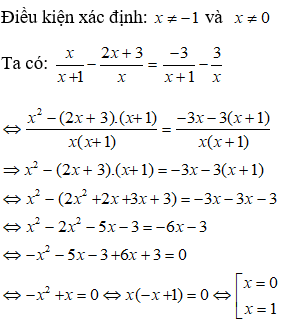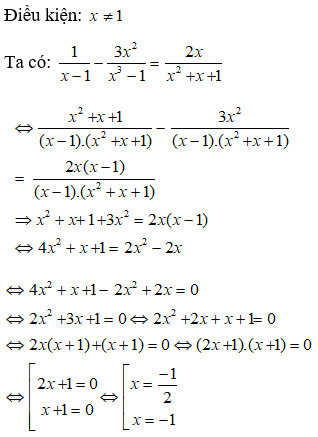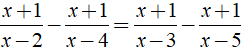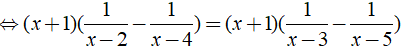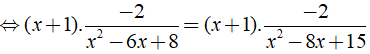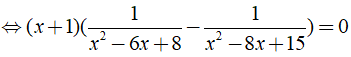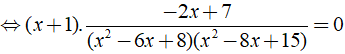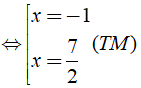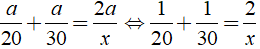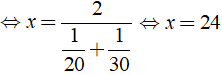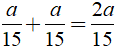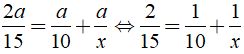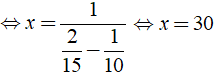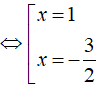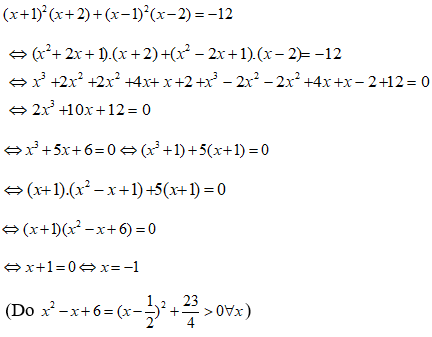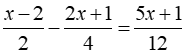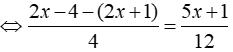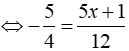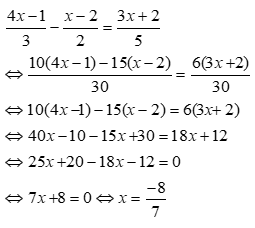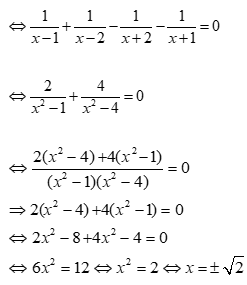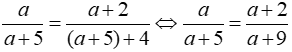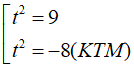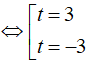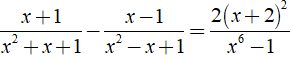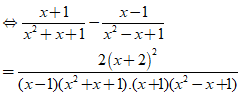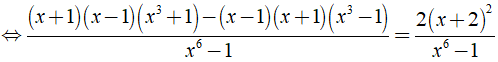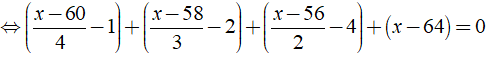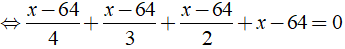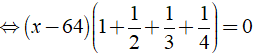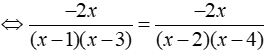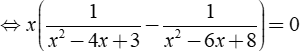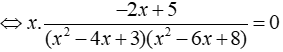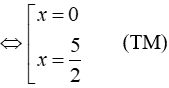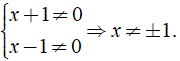Tổng hợp Lý thuyết & Trắc nghiệm Chương 3 Đại số 8
-
1791 lượt thi
-
68 câu hỏi
-
100 phút
Danh sách câu hỏi
Câu 1:
Một phương trình bậc nhất một ẩn có mấy nghiệm?
 Xem đáp án
Xem đáp án
Một phương trình bậc nhất một ẩn luôn có một nghiệm duy nhất.
(lưu ý vì đây là phương trình bậc nhất một ẩn nên a ≠ 0, do đó phương trình luôn có một nghiệm duy nhất. Không có trường hợp a = 0.)
Chọn đáp án B.
Câu 2:
Trong các phương trình sau, phương trình nào là phương trình một ẩn?
 Xem đáp án
Xem đáp án
+ Một phương trình với ẩn x là hệ thức có dạng A( x ) = B( x ), trong đó A( x ) gọi là vế trái, B( x ) gọi là vế phải.
+ Nghiệm của phương trình là giá trị của ẩn x thoả mãn (hay nghiệm đúng) phương trình.
Nhận xét:
+ Đáp án A: là phương trình một ẩn là x
+ Đáp án B: là phương trình hai ẩn là x,y
+ Đáp án C: là phương trình hai ẩn là a,b
+ Đáp án D: là phương trình ba ẩn là x,y,z
Chọn đáp án A.
Câu 3:
Nghiệm x = 2 là nghiệm của phương trình ?
 Xem đáp án
Xem đáp án
+ Đáp án A: 5x + 1 = 11 ⇔ 5x = 10 ⇔ x = 10/5 = 2 → Đáp án A đúng.
+ Đáp án B: - 5x = 10 ⇔ x = 10/ - 5 = - 2 → Đáp án B sai.
+ Đáp án C: 4x - 10 = 0 ⇔ 4x = 10 ⇔ x = 5/2 → Đáp án C sai.
+ Đáp án D: 3x - 1 = x + 7 ⇔ 3x - x = 7 + 1 ⇔ 2x = 8 ⇔ x = 4 → Đáp án D sai.
Chọn đáp án A.
Câu 4:
Trong các phương trình sau, cặp phương trình nào tương đương?
 Xem đáp án
Xem đáp án
Hai phương trình tương đương nếu chúng có cùng một tập hợp nghiệm.
Đáp án A:
+ Phương trình x = 2 có tập nghiệm S = { 2 }
+ Phương trình x( x - 2 ) = 0 ⇔ 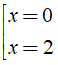
→ Hai phương trình không tương đương.
Đáp án B:
+ Phương trình x - 2 = 0 có tập nghiệm S = { 2 }
+ Phương trình 2x - 4 = 0 có tập nghiệm là S = { 2 }
Hai phương trình tương đương.
Đáp án C:
+ Phương trình 3x = 0 có tập nghiệm là S = { 0 }
+ Phương trình 4x - 2 = 0 có tập nghiệm là S = { 1/2 }
→ Hai phương trình không tương đương.
Đáp án D:
+ Phương trình ⇔ x = ± 3 có tập nghiệm là S = { ± 3 }
+ Phương trình 2x - 8 = 0 có tập nghiệm là S = { 4 }
→ Hai phương trình không tương đương.
Chọn đáp án B.
Câu 5:
Tập nghiệm của phương trình 4x - 12 = 0 là ?
 Xem đáp án
Xem đáp án
Ta có: 4x - 12 = 0 ⇔ 4x = 12 ⇔ x = 3
→ Phương trình có tập nghiệm là S = { 3 }
Chọn đáp án C.
Câu 6:
Phương trình có nghiệm là ?
 Xem đáp án
Xem đáp án
Ta có: - 1/2x = 5 ⇔ x = 5/( - 1/2) = - 10.
Vậy phương trình có tập nghiệm là x = - 10.
Chọn đáp án B.
Câu 7:
Nghiệm của phương trình 3x - 2 = - 7 là?
 Xem đáp án
Xem đáp án
Ta có: 3x - 2 = - 7 ⇔ 3x = - 7 + 2 ⇔ 3x = - 5
⇔ x = - 5/3
Vậy nghiệm của phương trình là x = - 5/3
Chọn đáp án B.
Câu 8:
Nghiệm của phương trình là?
 Xem đáp án
Xem đáp án
Ta có: y/5 - 5 = - 5 ⇔ y/5 = - 5 - ( - 5) ⇔ y/5 = 0
⇔ y = 5.0 ⇔ y = 0.
Vậy nghiệm của phương trình là y = 0.
Chọn đáp án C.
Câu 9:
Giá trị của m để phương trình 2x = m + 1 có nghiệm x = - 2 là?
 Xem đáp án
Xem đáp án
Phương trình 2x = m + 1 có nghiệm x = - 2
Khi đó ta có: 2.( - 2 ) = m + 1 ⇔ m + 1 = - 4 ⇔ m = - 5.
Vậy m = - 5 là giá trị cần tìm.
Chọn đáp án C.
Câu 10:
Tập nghiệm của phương trình - 4x + 7 = - 1 là?
 Xem đáp án
Xem đáp án
Ta có: - 4x + 7 = - 1 ⇔ - 4x = - 1 - 7 ⇔ - 4x = - 8
⇔ x = - 8/ - 4 ⇔ x = 2.
Vậy phương trình có tập nghiệm là S = { 2 }.
Chọn đáp án A.
Câu 11:
là nghiệm của phương trình nào sau đây?
 Xem đáp án
Xem đáp án
+ Đáp án A: 3x - 2 = 1 ⇔ 3x = 3 ⇔ x = 1 → Loại.
+ Đáp án B: 3x - 1 = 0 ⇔ 3x = 1 ⇔ x = 1/3 → Chọn.
+ Đáp án C: 4x + 3 = - 1 ⇔ 4x = - 4 ⇔ x = - 1 → Loại.
+ Đáp án D: 3x + 2 = - 1 ⇔ 3x = - 3 ⇔ x = - 1 → Loại.
Chọn đáp án B.
Câu 12:
Giá trị của m để cho phương trình sau nhận x = 2 làm nghiệm: 3x - 2m = x + 5 là:
 Xem đáp án
Xem đáp án
Phương trình 3x - 2m = x + 5 có nghiệm là x = 2
Khi đó ta có: 3.2 - 2m = 2 + 5 ⇔ 2m = - 1
⇔ m = - 1/2.
Vậy m = - 1/2 là giá trị cần tìm.
Chọn đáp án A.
Câu 13:
Nghiệm của phương trình là
 Xem đáp án
Xem đáp án
Phương trình
Vậy phương trình có nghiệm là x = 1
Chọn đáp án A.
Câu 14:
Nghiệm của phương trình là
 Xem đáp án
Xem đáp án
Phương trình
⇔ x + 2 = 0 ⇔ x = - 2
Vậy phương trình có nghiệm x = - 2
Chọn đáp án A.
Câu 15:
Giải phương trình sau: .
 Xem đáp án
Xem đáp án
Điều kiện xác định: x ≠ 2; x ≠ -1
Kết hợp điều kiện, vậy nghiệm phương trình đã cho là x = - 3
Chọn đáp án D
Câu 16:
Nghiệm của phương trình là
 Xem đáp án
Xem đáp án
Phương trình
Vậy phương trình có nghiệm x = 1
Chọn đáp án B.
Câu 17:
Nghiệm của phương trình - 8( 1,3 - 2x ) = 4( 5x + 1 ) là:
 Xem đáp án
Xem đáp án
Phương trình - 8( 1,3 - 2x ) = 4( 5x + 1 )
⇔ 4x + 72/5 = 0 ⇔ x = - 18/5
Vậy phương trình có nghiệm x = - 18/5
Chọn đáp án C.
Câu 19:
Nghiệm của phương trình là
 Xem đáp án
Xem đáp án
Phương trình
⇔ 8x + 5 - 2(3x + 1) = 2(2x + 1) + x + 4
⇔ 8x + 5 - 6x - 2 = 4x + 2 + x + 4
⇔ 2x + 3 = 5x + 6
⇔ - 3x - 3 = 0
⇔ x = - 1
Vậy phương trình có nghiệm x = - 1
Chọn đáp án C.
Câu 20:
Nghiệm của phương trình là
 Xem đáp án
Xem đáp án
Phương trình
Vậy phương trình có vô số nghiệm.
Chọn đáp án A.
Câu 21:
Tìm các giá trị của x để biểu thức sau có giá trị bằng 2:
 Xem đáp án
Xem đáp án
Điều kiện:
Để biểu thức đã cho có giá trị bằng 2 thì:
Kết hợp điều kiện phương trình đã cho có 2 nghiệm là x = 0 và
Chọn đáp án A
Câu 22:
Nghiệm của phương trình ( x - 2 )( x + 1 ) = 0 là:
 Xem đáp án
Xem đáp án
Phương trình ( x - 2 )( x + 1 ) = 0
Vậy nghiệm của phương trình là x = 2;x = - 1
Chọn đáp án D.
Câu 25:
Giá trị của m để phương trình ( x + 3 )( x + 1 - m ) = 4 có nghiệm x = 1 là?
 Xem đáp án
Xem đáp án
Do phương trình ( x + 3 )( x + 1 - m ) = 4 có nghiệm x = 1 nên ta có:
(1 + 3)(1 + 1 - m) = 4
⇔ 4(2 - m) = 4
⇔ 2 - m = 1
⇔ m = 1
Vậy m = 1.
Chọn đáp án A.
Câu 28:
Nghiệm của phương trình là:
 Xem đáp án
Xem đáp án
⇒ x = 3;x = 1
Vậy nghiệm của phương trình là x = 1;x = 3
Chọn đáp án B
Câu 29:
Tìm nghiệm của phương trình sau: .
 Xem đáp án
Xem đáp án
Kết hợp điều kiện thì nghiệm của phương trình đã cho là x = 1
Chọn đáp án D
Câu 30:
Giải phương trình sau:
 Xem đáp án
Xem đáp án
Kết hợp điều kiện ta được nghiệm của phương trình đã cho là x = -1 và
Chọn đáp án C
Câu 31:
Giá trị của m để phương trình (2x - m)/(3x + 1) = 2 có nghiệm x = 1 là?
 Xem đáp án
Xem đáp án
Phương trình (2x - m)/(3x + 1) = 2 có nghiệm x = 1 nên ta có:
(2.1 - m)/(3.1 + 1) = 2
⇔ (2 - m)/4 = 2
⇔ 2 - m = 8
⇔ m = - 6
Vậy m = - 6
Chọn đáp án B.
Câu 32:
Nghiệm của phương trình là
 Xem đáp án
Xem đáp án
ĐKXD: x ≠ {2, 3, 4, 5}
Phương trình
Vậy nghiệm của phương trình là x = - 1;x = 7/2
Chọn đáp án C.
Câu 33:
Tìm hai số tự nhiên chẵn liên tiếp biết biết tích của chúng là 24 là:
 Xem đáp án
Xem đáp án
Gọi 2 số chẵn liên tiếp cần tìm là x;x + 2 (x > 0;x ∈ Z)
Theo bài ra ta có: x(x + 2) = 24
⇔x(x + 6) - 4(x + 6) = 0
⇔ (x - 4)(x + 6) = 0 ⇔ x = 4 (Do x + 6 > 0∀ x > 0 )
Vậy hai số cần tìm là 4;6.
Chọn đáp án B.
Câu 34:
Một hình chữ nhật có chiều dài hơn chiều rộng 3cm. Chu vi hình chữ nhật là 100cm. Chiều rộng hình chữ nhật là:
 Xem đáp án
Xem đáp án
Gọi chiều rộng hình chữ nhật là x(cm) (x > 0)
→ Chiều dài hình chữ nhật là x + 3(cm)
Do chu vi hình chữ nhật là 100cm nên ta có:
2[ x + (x + 3) ] = 100 ⇔ 2x + 3 = 50 ⇔ x = 23,5
Vậy chiều rộng hình chữ nhật là 23,5cm
Chọn đáp án A.
Câu 35:
Một xe đạp khởi hành từ điểm A, chạy với vận tốc 15 km/h. Sau đó 6 giờ, một xe hơi đuổi theo với vận tốc 60 km/h. Hỏi xe hơi chạy trong bao lâu thì đuổi kịp xe đạp?
 Xem đáp án
Xem đáp án
Gọi t ( h ) là thời gian từ lúc xe hơi chạy đến lúc đuổi kịp xe đạp; t > 0.
⇒ t + 6 ( h ) là thời gian kể từ lúc xe đạp đi đến lúc xe hơi đuổi kịp.
+ Quãng đường xe đạp đi được là s1 = 15( t + 6 ) km.
+ Quãng đường xe hơi đi được là s2 = 60t km.
Vì hai xe xuất phát tại điểm A nên khi gặp nhau s1 = s2.
Khi đó ta có: 15(t + 6) = 60t ⇔ 60t - 15t = 90 ⇔ t = 2(h) (thỏa mãn)
Vậy xe hơi chạy được 2 giờ thì đuổi kịp xe đạp.
Chọn đáp án B.
Câu 36:
Một người đi từ A đến B. Trong nửa quãng đường đầu người đó đi với vận tốc 20km/h phần đường còn lại đi với tốc độ 30km/h. Vận tốc trung bình của người đó khi đi từ A đến B là:
 Xem đáp án
Xem đáp án
Gọi vận tốc trung bình của người đó là: x(km/h) (x > 0)
Gọi độ dài nửa quãng đường AB là: a(km)
Khi đó ta có:
+ Thời gian đi nửa quãng đường đầu là: a/20(h)
+ Thời gian đi nửa quãng đường sau là: a/30(h)
→ Thời gian đi cả quãng đường AB là:
Do đó ta có:
Vậy vận tốc cần tìm là 24km/h
Chọn đáp án B.
Câu 37:
Hai lớp A và B của một trường trung học tổ chức cho học sinh tham gia một buổi meeting. Người ta xem xét số học sinh mà một học sinh lớp A nói chuyện với học sinh lớp B thì thấy rằng: Bạn Khiêm nói chuyện với 5 bạn, bạn Long nói chuyện với 6 bạn, bạn Tùng nói chuyện với 7 bạn,…và đến bạn Hải là nói chuyện với cả lớp B. Tính số học sinh lớp B biết 2 lớp có tổng cộng 80 học sinh.
 Xem đáp án
Xem đáp án
Gọi số học sinh lớp A là x (0 < x < 80, x ∈ N)
Bạn thứ nhất của lớp A (Khiêm) nói chuyện với 4 + 1 bạn
Bạn thứ hai của lớp A (Long) nói chuyện với 4 + 2 bạn
Bạn thứ ba của lớp A (Tùng) nói chuyện với 4 + 3 bạn
…………………
Bạn thứ x của lớp A (Hải) nói chuyện với bạn
Do đó số học sinh lớp B là 4 + x
Vì 2 lớp có tổng cộng 80 học sinh nên ta có:
x + (4 + x) = 80
⇔ 2x - 76 = 0
⇔ x = 38
Vậy số học sinh lớp B là: 80 - 38 = 42 (Học sinh)
Chọn đáp án B.
Câu 38:
Khiêm đi từ nhà đến trường Khiêm thấy cứ 10 phút lại gặp một xe buýt đi theo hướng ngược lại. Biết rằng cứ 15 phút lại có 1 xe buýt đi từ nhà Khiêm đến trường là cũng 15 phút lại có 1 xe buýt đi theo chiều ngược lại. Các xe chuyển động với cùng vận tốc. Hỏi cứ sau bao nhiêu phút thì có 1 xe cùng chiều vượt qua Khiêm.
 Xem đáp án
Xem đáp án
Gọi thời gian phải tìm là x (Phút)
Gọi thời gian Khiêm đi từ nhà đến trường là a (Phút)
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng ngược lại là: a/10
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng cùng chiều là: a/x
Số xe đi qua Khiêm khi Khiêm đi từ nhà đến trường cũng chính là số xe đã đi trên đoạn đường từ nhà Khiêm đến trường theo cả 2 chiều là:
Ta có phương trình:
Vậy cứ sau 30 phút lại có xe cùng chiều vượt qua Khiêm.
Chọn đáp án C.
Câu 39:
Mẹ hơn con 24 tuổi. Sau 2 năm nữa thì tuổi mẹ gấp 3 lần tuổi con. Tuổi của con hiện nay là:
 Xem đáp án
Xem đáp án
Gọi số tuổi của con hiện tại là x (Tuổi) (x ∈ N*)
→ số tuổi của mẹ hiện nay là x + 24 (Tuổi)
Theo bài ra ta có: 3(x + 2) = x + 24 + 2
⇔ 2x - 20 = 0
⇔ x = 10
Vậy hiện tại tuổi của con là 10 tuổi.
Chọn đáp án B.
Câu 40:
Phương trình (1) và (2) có tương đương hay không?
(1) x - 1 = 4
(2) (x - 1)x = 4x
 Xem đáp án
Xem đáp án
Phương trình (1) x - 1 = 4 có tập nghiệm S1 = 5
Phương trình (2): (x - 1)x = 4x ⇔ (x - 1)x - 4x = 0 ⇔ (x - 5)x = 0
Phương trình (2) có tập nghiệm là S2 = 0;5
Vì S1 ≠ S2 nên hai phương trình (1) và (2) không tương đương.
Câu 41:
Tìm điều kiện của m để phương trình sau là phương trình bậc nhất một ẩn: (2m - 1)x + 3 - m = 0
 Xem đáp án
Xem đáp án
(2m - 1)x + 3 - m = 0 là phương trình bậc nhất một ẩn
⇔ 2m - 1 ≠ 0
⇔ m ≠ 1/2
Câu 42:
Tìm điều kiện của m để phương trình sau là phương trình bậc nhất một ẩn: (3m - 5)x + 1 - m = 0
 Xem đáp án
Xem đáp án
(3m - 5)x + 1 - m = 0 là phương trình bậc nhất một ẩn
⇔m ≠ 5/3
Câu 43:
Cho phương trình 2(x + 3) – 3 = 3 – x.
x = - 3 có thỏa mãn phương trình không
 Xem đáp án
Xem đáp án
Với x = -3 thì
VT = 2(x + 3) – 3 = 2(– 3 + 3) – 3 = 2. 0 – 3 = 0 – 3 = – 3
Ta có: VP = 3 – x = 3 – (– 3) = 6 ≠ – 3
Vậy x = - 3 không thỏa mãn phương trình
Câu 44:
Cho phương trình 2(x + 3) – 3 = 3 – x.
x = 0 có là một nghiệm của phương trình không?
 Xem đáp án
Xem đáp án
Với x = 0 thì
VT = 2(0 + 3) – 3 = 2.3 – 3 = 6 – 3 = 3
Ta có: VP = 3 – x = 3 – 0 = 3 = VT
⇒ x = 0 có là một nghiệm của phương trình
Vậy x = 0 là nghiệm của phương trình.
Câu 45:
Tìm giá trị của m sao cho phương trình sau nhận x = 2 làm nghiệm: 3x - 2m = x + 5.
 Xem đáp án
Xem đáp án
Phương trình 3x - 2m = x + 5 nhận x = 2 làm nghiệm nên ta có:
3.2 - 2m = 2 + 5
⇔ 2m = - 1 ⇔ m = - 1/2
Vậy m = - 1/2
Câu 46:
Tìm giá trị của m, biết rằng phương trình: nhận x = 2 làm nghiệm: 5m - 7x = 3x
 Xem đáp án
Xem đáp án
Phương trình 5m - 7x = 3x nhận x = 2 làm nghiệm nên ta có:
5m - 7.2 = 3.2 ⇔ 5m = 20 ⇔ m = 4
Vậy m = 4
Câu 47:
Giải phương trình: 3x + 1 = x + 2
 Xem đáp án
Xem đáp án
Phương trình ⇔ 2x - 1 = 0 ⇔ x = 1/2
Vậy phương trình có nghiệm x = 1/2
Câu 48:
Giải phương trình:
 Xem đáp án
Xem đáp án
Phương trình
⇔ - 8x + 4 = 0
⇔ x = 1/2
Vậy phương trình có nghiệm x = 1/2
Câu 50:
Giải phương trình: x(x + 3) = (3 - x)(1 + x)
 Xem đáp án
Xem đáp án
⇔ 2x(x - 1) + 3(x - 1) = 0
⇔ (x - 1)(2x + 3) = 0
Vậy tập nghiệm của phương trình là S = { - 3/2;1 }
Câu 53:
Giải các phương trình sau
 Xem đáp án
Xem đáp án
Ta có:
⇔ 5x + 1 = - 15 ⇔ x = - 16/5
Vậy tập nghiệm của phương trình là S = { - 16/5 }
Câu 55:
Giải phương trình:
 Xem đáp án
Xem đáp án
ĐKXĐ: x ≠ ± 1;x ≠ ± 2
Phương trình
Vậy tập nghiệm của phương trình là S = { ± √ 2 }
Câu 56:
Mẫu số của một phân số lớn hơn tử của nó là 5 đơn vị, nếu tăng cả tử thêm 2 đơn vị và mẫu thêm 4 đơn vị, thì được một phân số mới bằng phân số ban đầu . Tìm phân số cho ban đầu
 Xem đáp án
Xem đáp án
Gọi tử số của phân số ban đầu là a, theo bài ra ta có:
(Điều kiện: a ≠ - 5;a ≠ - 9 )
a(a + 9) = (a + 2)(a + 5)
⇔ 2a = 10 ⇔ a = 5 (Thỏa mãn)
Vậy phân số cần tìm là: 5/10
Câu 57:
Giải phương trình:
 Xem đáp án
Xem đáp án
⇔
Với t = 3 ⇒ x = - 1/2
Với t = - 3 ⇒ x = - 5/4
Vậy tập nghiệm của phương trình là S = { - 1/2; - 5/4 }
Câu 59:
Giải phương trình:
 Xem đáp án
Xem đáp án
Ta thấy x = 1 không phải nghiệm của phương trình nên nhân 2 vế của phương trình với x - 1 ta có:
⇔ x = 1(KTM)
Vậy phương trình đã cho vô nghiệm.
Câu 61:
Giải các phương trình sau:
 Xem đáp án
Xem đáp án
ĐKXĐ: x ≠ 1 hoặc x = -1.
Ta có:
⇔ 8x = - 10 ⇔ x = - 5/4.
Vậy phương trình đã cho có nghiệm là x = - 5/4.
Câu 62:
Giải các phương trình sau
 Xem đáp án
Xem đáp án
Ta có:
⇔ x - 64 = 0 ⇔ x = 64
Vậy phương trình đã cho có nghiệm là x = 64
Câu 63:
Giải phương trình
 Xem đáp án
Xem đáp án
ĐKXĐ: x ≠ 1;x ≠ 2;x ≠ 3;x ≠ 4
Phương trình
Vậy tập nghiệm của phương trình là S = { 0;5/2 }
Câu 65:
Giải các phương trình sau:
 Xem đáp án
Xem đáp án
ĐKXĐ:
Ta có:
⇔ 2x = 6 ⇔ x = 3.
Vậy phương trình đã cho có nghiệm là x = 3.