Trắc nghiệm Toán 8 KNTT Bài 12. Hình bình hành có đáp án
-
327 lượt thi
-
15 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
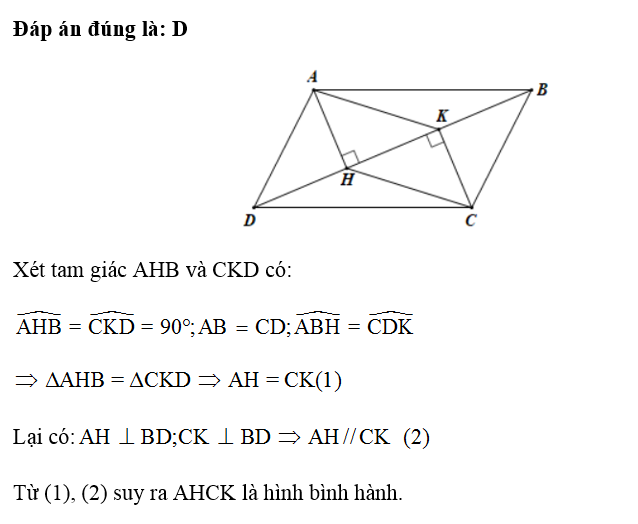
Đáp án đúng là: D
Dấu hiệu nhận biết: Tứ giác có các cạnh đối song song là hình bình hành.
Câu 2:
Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Dấu hiệu nhận biết:
+ Tứ giác có các cạnh đối song song là hình bình hành nên A đúng.
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành nên C đúng.
+ Tứ giác có các góc đối bằng nhau là hình bình hành nên D đúng.
Câu 3:
Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Dấu hiệu nhận biết:
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành nên A đúng.
+ Hình thang nên hai cạnh đối song song, thêm điều kiện hai cạnh bên song song tức có các cặp cạnh đối song song nên hình thang này là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành nên D đúng.
Câu 4:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Trong hình bình hành các góc đối bằng nhau: và
Nên
Hình bình hành có các góc đối bằng nhau
Câu 7:
Chu vi của hình bình hành ABCD bằng 10 cm, chu vi của tam giác ABD bằng 9 cm. Khi đó độ dài BD là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Vì chu vi của hình bình hành ABCD bằng 10 cm nên:
AB + BC + CD + DA = 10
Chu vi của tam giác ABD bằng 9 cm nên:
Câu 8:
Hãy chọn câu đúng. Cho hình bình hành ABCD, gọi E là trung điểm của AB, F là trung điểm của CD. Khi đó:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
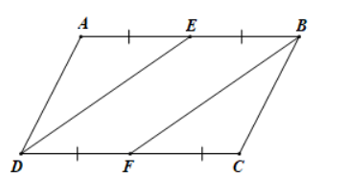
Vì ABCD là hình bình hành nên AB // CD; AB = CD
Xét tứ giác BEDF có BE = FD; BE // FD (do AB // CD) nên BFDE là hình bình hành.
Từ đó: DE = BF (tính chất hình bình hành)
Câu 10:
Tỉ số độ dài hai cạnh của hình bình hành là 3 : 5. Còn chu vi của nó bằng 48cm. Độ dài cạnh kề của hình bình hành là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Gọi độ dài hai cạnh của hình bình hành là a và b với a, b > 0
Theo bài ra ta có:
Nửa chu của hình bình hành là: 48 : 2 = 24 cm
Suy ra: a + b = 24 cm. Theo tính chất của dãy tỉ số bằng nhau ta có:
Þ a = 3.3 = 9; b = 3.5 = 15
Vậy hai cạnh của hình bình hành là 9 cm và 15cm.
Câu 11:
Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm E và F sao cho . Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
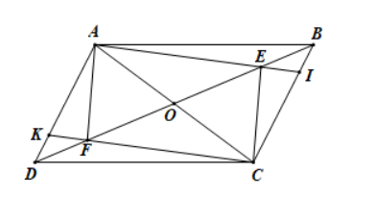
Gọi O là giao điểm của AC và BD. Ta có OA = OC, OB = OD
Mà BE = DF (gt) Þ OE = FO.
Tứ giác AECF có hai đường chéo AC và EF cắt nhau tại trung điểm O nên AECF là hình bình hành
Þ FA = CE
Câu 13:
Hình bình hành ABCD có . Số đo góc A bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có ABCD là hình bình hành nên mà
Câu 15:
Cho tứ giác ABCD. Gọi E, F lần lượt là giao điểm của AB và CD; M, N, P, Q lần lượt là thuộc các cạnh AF, EC, BF, DE và . Khi đó MNPQ là hình gì? Khẳng định nào sau đây là đúng nhất?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
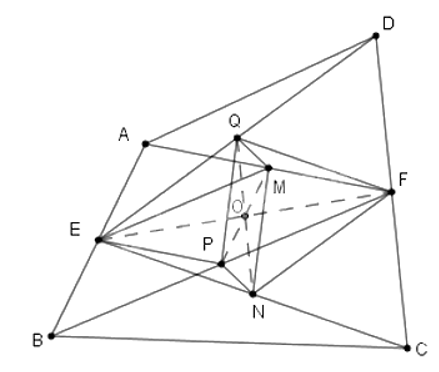
Nối EF; EP, FQ, EM, PM, QN. Gọi O là giao của QN và EF.
Xét tam giác CED ta có:
Þ NFQE là hình bình hành nên hai đường chéo QN và EF giao nhau tại trung điểm của mỗi đường. Suy ra O là trung điểm của QN và EF (1)
Xét tam giác ABF ta có:
Þ EMFB là hình bình hành nên hai đường chéo PM và EF giao nhau tại trung điểm của mỗi đường. Mà O là trung điểm của EF nên O cũng là trung điểm của PM (2)
Từ (1) và (2) suy ra: tứ giác QMNP có hai đường chéo QN, PM giao nhau tại trung điểm O mỗi đường nên QMNP là hình bình hành.