15 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa kì 1 Toán 8 CD có đáp án (Đề 1)

Câu 1:

Biểu thức nào sau đây là đơn thức thu gọn?

A. $- 5 x y^{2}$

B. $x y z + x z$

C. $2 (x^{2} + y^{2})$

D. $- 3 x 4 y x z$

Xem đáp án

Đáp án đúng là: A

Biểu thức $- 5 x y^{2}$ là đơn thức thu gọn;

Biểu thức $x y z + x z$ và $2 (x^{2} + y^{2})$ là đa thức.

Biểu thức $- 3 z 4 y x z$ là đơn thức chưa thu gọn.

Câu 2:

Cho các đơn thức $A = 4 x^{3} y (- 5 x y), B = - 17 x^{4} y^{2}, C = \frac{3}{5} x^{6} y$ . Các đơn thức nào sau đây đồng dạng với nhau?

A. Đơn thức A và đơn thức C;

B. Đơn thức B và đơn thức C;

C. Đơn thức A và đơn thức B;

D. Cả ba đơn thức A, B, C đồng dạng với nhau.

Xem đáp án

Đáp án đúng là: C

Ta có: $A = 4 x^{3} y (- 5 x y) = - 20 x^{4} y^{2}$ nên suy ra A và B là hai đơn thức đồng dạng, nhưng không đồng dạng với đơn thức C.

Câu 3:

Cho biểu thức $A = - 2 y + 2 x^{3} + 8 y - 35 - x^{3} .$ Giá trị của biểu thức A tại $x = 3, y = - 4$ là

A. -32

B. -28

C. 16

D. 86

Xem đáp án

Đáp án đúng là: A

Ta có: $A = - 2 y + 2 x^{3} + 8 y - 35 - x^{3} = x^{3} + 6 y - 35$

Thay $x = 3, y = - 4$ vào biểu thức A thu gọn ở trên ta được:

$A = 3^{3} + 6. (- 4) - 35 = 9 - 24 - 35 = - 32$ .

Câu 4:

Hằng đẳng thức $A^{2} - B^{2} = (A - B) (A + B)$ có tên là

A. bình phương của một tổng;

B. bình phương của một hiệu;

C. tổng hai bình phương;

D. hiệu hai bình phương.

Xem đáp án

Đáp án đúng là: D

Hằng đẳng thức $A^{2} - B^{2} = (A - B) (A + B)$ có tên là hiệu hai bình phương.

Câu 5:

Quy đồng mẫu thức hai phân thức $\frac{2}{x^{2} y}$ và $\frac{3}{x y^{2}}$ ta được mẫu thức chung là

A. $x^{2} y$

B. $x y^{2}$

C. $x^{2} y^{2}$

D. $x^{3} y^{3}$

Xem đáp án

Đáp án đúng là: C

Mẫu thức chung của hai phân thức $\frac{2}{x^{2} y}$ và $\frac{3}{x y^{2}}$ là $x^{2} y^{2} .$

Câu 6:

Kết quả của phép tính $\frac{a - 2}{a - b} - \frac{2 - b}{b - a}$ là

A. -1

B. 1

C. $\frac{a - b}{b - a}$

D. $\frac{a + b - 4}{a - b}$

Xem đáp án

Đáp án đúng là: B

Ta có: $\frac{a - 2}{a - b} - \frac{2 - b}{b - a} = \frac{a - 2}{a - b} + \frac{2 - b}{a - b} = \frac{a - 2 + 2 - b}{a - b} = \frac{a - b}{a - b} = 1.$

Câu 7:

Hình nào sau đây là hình chóp tam giác đều?

A. Hình có đáy là tam giác;

B. Hình có đáy là tam giác đều;

C. Hình có đáy là tam giác đều và tất cả các cạnh đều vuông góc với mặt đáy;

D. Hình có đáy là tam giác đều và tất cả các cạnh bên bằng nhau.

Xem đáp án

Đáp án đúng là: D

Hình có đáy là tam giác đều và tất cả các cạnh bên bằng nhau là hình chóp tam giác đều.

Câu 8:

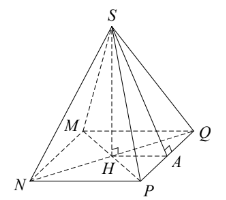
Cho hình vẽ bên, trung đoạn của hình chóp tứ giác S.MNPQ là

Cho hình vẽ bên, trung đoạn của hình chóp tứ giác S.MNPQ là (ảnh 1)

A. SH;

B. SA;

C. HA;

D. NQ hoặc MP.

Xem đáp án

Đáp án đúng là: B

Trung đoạn của hình chóp tứ giác S.MNPQ là đoạn thẳng SA.

Câu 9:

Thu gọn biểu thức:

a) $65 x^{9} y^{5} : (- 13 x^{4} y^{4});$

b) $x (x - y) - y (y^{2} - x);$

c) $(x - y) (x^{2} + y^{2}) - (x^{4} y - x y^{4}) : x y$ .

Xem đáp án

a) $65 x^{9} y^{5} : (- 13 x^{4} y^{4})$

$= - 5 x^{5} y$ .

b) $x (x - y) - y (y^{2} - x)$

$= x^{2} - x y - y^{3} + x y$

$= x^{2} - y^{3} .$

c) $(x - y) (x^{2} + y^{2}) - (x^{4} y - x y^{4}) : x y$

$= x^{3} + x y^{2} - (x^{2} y + y^{3}) - (x^{3} - y^{3})$

$= x^{3} + x y^{2} - x^{2} y - y^{3} - x^{3} + y^{3}$

$= x y^{2} - x^{2} y$

Câu 10:

a) $5 (y - 3) - x (3 - y)$ ; b) $- 9 + 6 x - x^{2};$ c) $x^{3} + 27 + (x + 3) (x - 9)$ .

Xem đáp án

a) $5 (y - 3) - x (3 - y)$

$= 5 (y - 3) + x (y - 3)$

$= (y - 3) (5 + x) .$

b) $- 9 + 6 x - x^{2}$

$= - (9 - 6 x + x^{2})$

$= - {(3 - x)}^{2} .$

c) $x^{3} + 27 + (x + 3) (x - 9)$

$= (x + 3) (x^{2} - 3 x + 9) + (x + 3) (x - 9)$

$= (x + 3) (x^{2} - 3 x + 9 + x - 9)$

$= (x + 3) (x^{2} - 2 x)$

$= (x + 3) x (x - 2)$

Câu 11:

a) Tìm điều kiện xác định của biểu thức A

b) Tìm biểu thức C sao cho C = A - B với

B = \frac{x}{x - 2} + \frac{9 x + 2}{4 - x^{2}}

(x \neq \pm 2) .

Xem đáp án

a) Điều kiện xác định của biểu thức A là $x + 2 \neq 0$ hay $x \neq - 2.$

b) Với $x \neq \pm 2$ , ta có: $C = A - B$

Suy ra $C = \frac{x - 2}{x + 2} - (\frac{x}{x - 2} + \frac{9 x + 2}{4 - x^{2}})$

$C = \frac{x - 2}{x + 2} - \frac{x}{x - 2} - \frac{9 x + 2}{4 - x^{2}}$

$= \frac{x - 2}{x + 2} - \frac{x}{x - 2} + \frac{9 x + 2}{x^{2} - 4}$ $= \frac{{(x - 2)}^{2} - x (x + 2) + 9 x + 2}{(x + 2) (x - 2)}$

$= \frac{x^{2} - 4 x + 4 - x^{2} - 2 x + 9 x + 2}{(x + 2) (x - 2)}$

$= \frac{3 x + 6}{(x + 2) (x - 2)}$

$= \frac{3 (x + 2)}{(x + 2) (x - 2)} = \frac{3}{x - 2}$

.

Câu 12:

c) Tính giá trị của biểu thức C khi $3 x (2 x + 1) - 6 (2 x + 1) = 0.$

Xem đáp án

c) Ta có: $3 x (2 x + 1) - 6 (2 x + 1) = 0$

$(2 x + 1) (3 x - 6) = 0$

$2 x + 1 = 0$ hoặc $3 x - 6 = 0$

$x = - \frac{1}{2}$ (thỏa mãn) hoặc $x = 2$ (không thỏa mãn).

Thay $x = - \frac{1}{2}$ vào biểu thức $C = \frac{3}{x - 2}$ ta được:

$C = \frac{3}{- \frac{1}{2} - 2} = \frac{3}{- \frac{5}{2}} = \frac{- 6}{5} .$

Câu 13:

Cho tứ giác ABCD biết $\hat{A} = 75 °$ , $\hat{B} = 90 °$ , $\hat{C} = 120 °$ . Tính số đo các góc ngoài tại đỉnh D của tứ giác ABCD.

Xem đáp án

Xét tứ giác ABCD, ta có $\hat{A} + \hat{B} + \hat{C} + \hat{D} = 360 °$

Do đó $75 ° + 90 ° + 120 ° + \hat{D} = 360 °$

Hay $285 ° + \hat{D} = 360 °$

Suy ra $\hat{D} = 360 ° - 285 ° = 75 °$

Khi đó góc ngoài tại đỉnh D của tứ giác là $180 ° - 75 ° = 105 ° .$

Câu 14:

Bạn Nam đo một chiếc đèn thả trang trí như hình vẽ bên thì nhận thấy các cạnh đều có cùng độ dài là 20 cm.

a) Tính độ dài trung đoạn của hình chóp.

b) Tính diện tích xung quanh của chiếc đèn.

c) Bạn Nam đọc và thấy rằng khi treo đèn thì khoảng cách từ đáy của đèn cách mặt trền là 1 m là tốt nhất. Vậy bạn Nam cần đưa đoạn dây điện từ đầu đèn (vị trí A) tới mặt trần là bao nhiêu (làm tròn kết quả đến hàng phần mười)?

Bạn Nam đo một chiếc đèn thả trang trí như hình vẽ bên thì nhận thấy các cạnh đều có cùng độ dài là 20 cm. a) Tính độ dài trung đoạn của hình chóp. (ảnh 1)

Xem đáp án

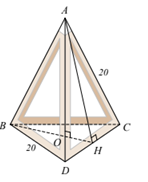
Bạn Nam đo một chiếc đèn thả trang trí như hình vẽ bên thì nhận thấy các cạnh đều có cùng độ dài là 20 cm. a) Tính độ dài trung đoạn của hình chóp. (ảnh 2)

a) Chiếc đèn được mô phỏng thành hình chóp tam giác đều ABCD như hình vẽ. Gọi AH là trung đoạn kẻ từ đỉnh A của hình chóp.

Theo bài ta có: $A B = A C = A D = 20$ cm

$B C = C D = D B = 20$ cm.

$Δ A C D$ đều nên AH vừa là đường cao vừa là đường trung tuyến.

Do đó $D H = C H = \frac{1}{2} C D = 10$ cm.

Xét $Δ A H C$ vuông tại H, theo định lí Pythagore ta có:

$A H^{2} = A C^{2} - C H^{2} = 20^{2} - 10^{2} = 300$

Suy ra

A H = \sqrt{300} = \sqrt{100.3} = \sqrt{{(10 \sqrt{3})}^{2}} = 10 \sqrt{3}

cm.

b) Chu vi đáy của hình chóp là: $C = 3 B D = 3.20 = 60$ cm.

Diện tích xung quanh của chiếc đèn là:

$S_{x q} = \frac{1}{2} C . A H = \frac{1}{2} .60.10 \sqrt{3} = 300 \sqrt{3}$ cm².

c) Vì $Δ A D C$ và $Δ B D C$ đều là các tam giác đều có cạnh 20 cm nên hai đường cao AH và BH của hai tam giác bằng nhau.

Vì O là trọng tâm $Δ B D C$ nên $O H = \frac{1}{3} B H = \frac{10 \sqrt{3}}{3}$ cm.

$Δ A O H$ vuông tại O, theo định lí Pythagore ta có:

$A O^{2} = A H^{2} - O H^{2} = 300 - {(\frac{10 \sqrt{3}}{3})}^{2} = 300 - \frac{300}{9} = \frac{800}{3}$

Suy ra $A O = \sqrt{\frac{800}{3}} \approx 16,3$ cm.

Khi đó bạn Nam cần đưa dây diện từ đầu đèn tới trần nhà khoảng là $100 - 16,3 = 83,7$ cm.

Câu 15:

Cho các số thực a, b, c thỏa mãn ab + bc + ca = 2025. Chứng minh rằng

$\frac{a^{2} - b c}{a^{2} + 2025} + \frac{b^{2} - c a}{b^{2} + 2025} + \frac{c^{2} - a b}{c^{2} + 2025} = 0$ .

Xem đáp án

Ta có: $a^{2} + 2025 = a^{2} + a b + b c + c a = (a + b) (c + a)$

Khi đó $\frac{a^{2} - b c}{a^{2} + 2025} = \frac{a^{2} - b c}{(a + b) (c + a)} .$

Tương tự ta cũng có: $\frac{b^{2} - c a}{b^{2} + 2025} = \frac{b^{2} - c a}{(a + b) (b + c)}; \frac{c^{2} - a b}{c^{2} + 2025} = \frac{c^{2} - a b}{(b + c) (c + a)}$

Suy ra $P = \frac{a^{2} - b c}{a^{2} + 2025} + \frac{b^{2} - c a}{b^{2} + 2025} + \frac{c^{2} - a b}{c^{2} + 2025}$

$= \frac{a^{2} - b c}{(a + b) (c + a)} + \frac{b^{2} - c a}{(b + c) (a + b)} + \frac{c^{2} - a b}{(c + a) (b + c)}$

$= \frac{(a^{2} - b c) (b + c) + (b^{2} - c a) (c + a) + (c^{2} - a b) (a + b)}{(a + b) (b + c) (c + a)}$

$= \frac{a^{2} b + a^{2} c - b^{2} c - b c^{2} + b^{2} c + b^{2} a - c^{2} a - c a^{2} + c^{2} a + c^{2} b - a^{2} b - a b^{2}}{(a + b) (b + c) (c + a)} = 0$ .