12 câu hỏi trắc nghiệm thuộc Bài tập Hình thang (có lời giải chi tiết)

Câu 1:

Chọn câu đúng trong các câu sau:

A. Hình thang có ba góc tù, một góc nhọn.

B. Hình thang có ba góc vuông, một góc nhọn.

C. Hình thang có ba góc nhọn, một góc tù.

D. Hình thanh có nhiều nhất hai góc nhọn và nhiều nhất hai góc tù.

Xem đáp án

Do hai góc kề một cạnh bên của hình thang có tổng bằng $180 °$ .

Do đó sẽ có các trường hợp sau: 1 góc tù – 1 góc nhọn, 2 góc vuông

Do có 2 cặp góc như vậy nên hình thang có nhiều nhất hai góc nhọn và nhiều nhất hai góc tù.

Chọn đáp án D.

Câu 2:

Hình thang ABCD có $\hat{C} + \hat{D} = 150^{0}$ . Khi đó $\hat{A} + \hat{B} = ?$

A. $220^{0}$

B. $210^{0}$

C. $200^{0}$

D. $190^{0}$

Xem đáp án

Câu 3:

Cho hình thang ABCD trong đó có $\hat{A} = 120^{0}, \hat{B} = 60^{0}, \hat{D} = 135^{0}$ thì số đo của góc C = ?

A. $55^{0}$

B. $45^{0}$

C. $50^{0}$

D. $60^{0}$

Xem đáp án

Câu 4:

Cho hình thang ABCD có AB // CD. Biết $\hat{A} = 100^{o}$ , tính $\hat{D}$

A. $80^{o}$

B. $100^{o}$

C. $120^{o}$

D. $50^{o}$

Xem đáp án

Vì tứ giác ABCD là hình thang với (AB // CD) nên $\hat{A} + \hat{D} = 180 °$ (hai góc kề một cạnh bên)

Mà $\hat{A} = 100 °$ nên $\hat{D} = 180 ° - 100 ° = 80 °$

Chọn A

Câu 5:

Cho hình thang ABCD có AB // CD và $\hat{A} = 120^{o}, \hat{B} = 120^{o}$ . Tính $\hat{C}, \hat{D}$

A. $\hat{C} = 60 °, \hat{D} = 60 °$

B. $\hat{C} = 60 °, \hat{D} = 90 °$

C. $\hat{C} = 90 °, \hat{D} = 60 °$

D. $\hat{C} = 60 °, \hat{D} = 75 °$

Xem đáp án

Vì tứ giác ABCD là hình thang và $A B / / C D$ nên

$\hat{A} + \hat{D} = 180 °$ (hai góc kề một cạnh bên)

Mà $\hat{A} = 120 °$ nên $\hat{D} = 180 ° - 120 ° = 60 °$

Tương tự, $\hat{B} + \hat{C} = 180 °$ do đó $\hat{C} = 60 °$

Chọn A

Câu 6:

Cho hình thang vuông ABCD vuông tại A và D. Biết AD = 3 cm và CD = 4cm. Tính AC?

A. 3cm

B. 4cm

C. 3,5cm

D. 5cm

Xem đáp án

Do tứ giác ABCD là hình thang vuông nên $\hat{D} = 90 °$ . Suy ra, tam giác ADC là tam giác vuông tại D.

Áp dụng định lí Pi-ta-go vào tam giác ACD vuông tại D ta có:

$A C^{2} = A D^{2} + D C^{2} = 3^{2} + 4^{2} = 25$

Suy ra $A C = 5 c m$

Chọn đáp án D.

Câu 7:

Cho tứ giác lồi ABCD có AB // CD và AD = 6cm; DC = 8cm và AC = 10cm. Tìm khẳng định sai ?

A. Tam giác ADC vuông tại D.

B. Tứ giác ABCD là hình thang

C. Tứ giác ABCD là hình thang vuông có $\hat{B} = 90^{o}$

D. Tứ giác ABCD là hình thang vuông có $\hat{D} = 90^{o}$

Xem đáp án

Tứ giác ABCD có AB // CD nên tứ giác ABCD là hình thang có 2 đáy là AB và CD.

Xét tam giác ACD có

Câu 8:

Cho hình thang ABCD có AB // CD và $\hat{A} = 2 \hat{D}$ . Tính góc A?

A. $60^{o}$

B. $120^{o}$

C. $90^{o}$

D. $80^{o}$

Xem đáp án

Vì tứ giác ABCD là hình thang có $A B / / C D$ nên

$\hat{A} + \hat{D} = 180 °$ (hai góc kề một cạnh bên)

Mà $\hat{A} = 2 \hat{D}$ nên $2 \hat{D} + \hat{D} = 180 ° \Leftrightarrow 3 \hat{D} = 180 °$

Suy ra $\hat{D} = 60 °$ và $\hat{A} = 120 °$

Chọn B

Câu 9:

Cho hình thang ABCD có AB // CD và $\hat{C} - \hat{B} = 30^{o}$ . Tính góc C?

A. $105^{o}$

B. $90^{o}$

C. $75^{o}$

D. $60^{o}$

Xem đáp án

Câu 10:

Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho DE // BC. Chọn đáp án đúng nhất. Tứ giác BDEC là hình gì?

A. Hình thang

B. Hình thang vuông

C. Hình thang cân

D. Cả A, B, C đều sai

Xem đáp án

Đáp án cần chọn là: C

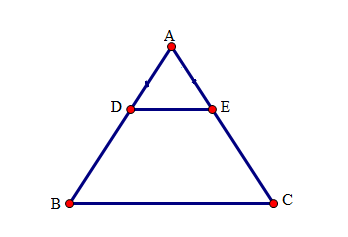
Tứ giác BDEC có DE // BC nên tứ giác BDEC là hình thang.

Lại có $\hat{A B C} = \hat{A C B}$ (vì tam giác ABC cân tại A) nên BDEC là hình thang cân

Câu 11:

Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB, AC lần lượt tại D và E. Chọn khẳng định đúng nhất?

A. Tứ giác BDIC là hình thang

B. Tứ giác BIEC là hình thang

C. Tứ giác BDEC là hình thang

D. Cả A, B, C đều đúng

Xem đáp án

Đáp án cần chọn là: D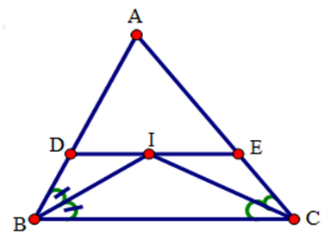

Xét tứ giác DECB có: DE // BC (gt) nên tứ giác DECB là hình thang.

Tương tự:

Tứ giác DICB có DI // BC (gt) nên tứ giác DICB là hình thang.

Tứ giác IECB có IE // CB (gt) nên tứ giác IECB là hình thang.

Câu 12:

Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB, AC lần lượt tại D và E.

Chọn khẳng định đúng

A. DE > BD + CE

B. DE = BD + CE

C. DE < BD + CE

D. BC = BD + CE

Xem đáp án

Đáp án cần chọn là: B

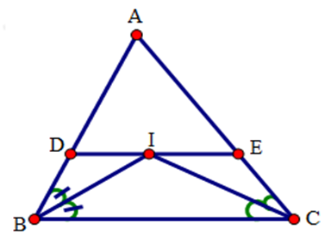
Vì DE // BC (gt) nên suy ra $\hat{D I B} = \hat{I B C}$ (so le trong)

Mà $\hat{D B I} = \hat{I B C}$ (gt) nên $\hat{D I B} = \hat{D B I}$

Suy ra tam giác BDI cân đỉnh D.

Do đó DI = DB (1)

Ta có: IE // CB nên suy ra $\hat{E I C} = \hat{B C I}$ (so le trong)

Mà $\hat{B C I} = \hat{E C I}$ (gt) nên $\hat{E C I} = \hat{E I C}$

Suy ra tam giác EIC cân đỉnh E

Do đó EI = EC (2)

Cộng (1) và (2) vế theo vế ta được: DI + EI = BD + CE

=> DE = BD + CE