Trắc nghiệm chuyên đề Toán 8 Chủ đề 1. Đa giác. Đa giác đều có đáp án
-
834 lượt thi
-
6 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho đa giác đều có 14 cạnh. Tính :
a) Tổng số đo góc của đa giác đó
Xem đáp án
a) Tổng số đo các góc của đa giác n cạnh là ( n - 2 ).1800.
Tổng số đo của đa giác 14 cạnh là ( 14 - 2 ).1800 = 21600.
Câu 2:
b) Số đo một góc của đa giác
Xem đáp án
b) Số đo của một góc của đa giác đều n cạnh là
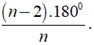
Số đo một góc của đa giác 14 cạnh là
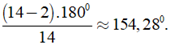
Câu 3:
c) Số đường chéo của đa giác.
Xem đáp án
c) Số đường chéo của đa giác n cạnh là
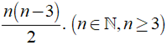
Số đường chéo của đa giác 14 cạnh là
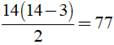đường chéoCâu 4:
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?
A. Hình vuông là đa giác đều.
B. Tổng các góc của đa giác lồi 8 cạnh là 10800.
C. Hình thoi là đa giác đều.
D. Số đo góc của hình bát giác đều là 135,50.
Xem đáp án
Ta cần nhớ định nghĩa: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
+ Hình vuông là hình có 4 cạnh bằng nhau và 4 góc bằng nhau
⇒ Hình vuông là đa giác đều.
⇒ Đáp án A đúng.
+ Hình thoi là hình có 4 cạnh bằng nhau nhưng 4 góc không bằng nhau.
⇒ Hình thoi không phải là đa giác đều.
⇒ Đáp án C sai.
+ Tổng số đo các góc của đa giác n cạnh là ( n - 2 ).1800.
Khi đó tổng các góc của đa giác lồi 8 cạnh là ( 8 - 2 ).1800 = 10800.
⇒ Đáp án B đúng.
+ Số đo của một góc của đa giác đều n cạnh là (( n - 2 ).1800)/n.
Khi đó số đo của hình bát giác đều là (( 8 - 2 ).1800)/8 = 1350.
⇒ Đáp án D sai.
Câu 5:
Một đa giác 7 cạnh thì số đường chéo của đa giác đó là ?
Xem đáp án
Chọn đáp án C.
Số đường chéo của đa giác n cạnh là .
Khi đó số đường chéo của đa giác 7 cạnh là = 14 (đường chéo)
Câu 6:
Xem đáp án
Đáp án A
Số đường chéo của đa giác n cạnh là . ( n ∈ N, n ≥ 3 )
Theo giả thiết ta có = n ⇔ n( n - 3 ) = 2n ⇔ n2 - 3n - 2n = 0
⇔ n2 - 5n = 0 ⇔ n( n - 5 ) = 0 ⇔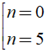 
So sánh điều kiện ta có n = 5 thỏa mãn