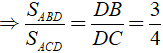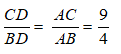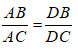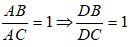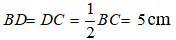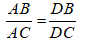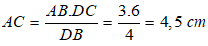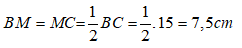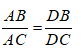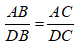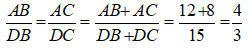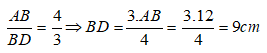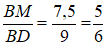16 câu hỏi trắc nghiệm thuộc Bài tập Tính chất đường phân giác của tam giác (có lời giải chi tiết)

Câu 1:

Cho Δ ABC vuông tại A có AB = 3 cm, BC = 5 cm, AD là đường phân giác của Δ ABC. Chọn phát biểu đúng?

A. BD = 20/7 cm; CD = 15/7 cm

B. BD = 15/7 cm; CD = 20/7 cm

C. BD = 1,5 cm; CD = 2,5 cm

D. BD = 2,5 cm; CD = 1,5 cm

Xem đáp án

Áp dụng định lý Py – ta – go ta có: $A C = \sqrt{(B C^{2} - A B^{2})} = \sqrt{(5^{2} - 3^{2})} = 4 (c m)$

Δ ABC, AD là đường phân giác của góc BACˆ ( D ∈ BC )

Ta có: DB/DC = AB/AC hay DB/AB = DC/AC

Khi đó ta có: DB/DC = AB/AC ⇒ DB/(DB + DC) = AB/(AB + AC)

hay DB/5 = 3/(3 + 4) ⇒ DB = 15/7 cm; DC = 20/7 ( cm )

Chọn đáp án B.

Câu 2:

Cho Δ ABC có BD là đường phân giác, AB = 8 cm, BC = 10 cm, AC = 6cm. Chọn phát biểu đúng?

A. DA = 8/3 cm, DC = 10/3 cm

B. DA = 10/3 cm, DC = 8/3 cm

C. DA = 4 cm, DC = 2 cm

D. DA = 3,5 cm, DC = 2,5 cm

Xem đáp án

BD là đường phân giác của Δ ABC

Ta có: DA/DC = AB/BC ⇔ DA/(DA + DC) = AB/(AB + BC)

Hay DA/6 = 8/(8 + 10) ⇒ DA = (6.8)/18 = 8/3 ( cm ); DC = 10/3 (cm)

Chọn đáp án A.

Câu 3:

Cho Δ ABC. Tia phân giác góc trong của góc A cắt BC tại D. Cho AB = 6, AC = x, BD = 9, BC = 21. Tính kết quả đúng của độ dài cạnh x

A. x = 14

B. x = 12

C. x = 8

D. x = 6

Xem đáp án

ΔABC có AD là phân giác trong của góc A.

Ta có: DB/DC = AB/AC ⇒ DB/(BC - DB) = AB/AC

Hay 9/(21 - 9) = 6/x ⇒ x = (12.6)/9 = 8

Chọn đáp án C.

Câu 4:

Cho tam giác ABC có AB = 15 cm, AC = 20 cm. Đường phân giác BACˆ cắt BC tại D. Tỉ số diện tích của Δ ABD và Δ ACD là?

A. 1/4

B. 1/2

C. 3/4

D. 1/3

Xem đáp án

Đường phân giác BACˆ cắt BC tại D

Ta có: DB/DC = AB/AC = 15/20 = 3/4

Chọn đáp án C.

Câu 5:

Cho tam giác ABC có AB = 4cm ; AC = 9cm.Gọi AD là tia phân giác của $\hat{B A C}$ . Tính tỉ số CD/BD

A. $\frac{7}{4}$

B. $\frac{9}{4}$

C. 1

D. $\frac{5}{4}$

Xem đáp án

Áp dụng tính chất đường phân giác của tam giác ABC ta có:

Chọn đáp án B

Câu 6:

Cho tam giác ABC có AC = 4cm, AB = 6cm và BC = 8cm. Gọi AD là tia phân giác của $\hat{B A C}$ . Tính BD?

A. 4,2 cm

B. 4,8cm

C. 5,2cm

D. 5,4cm

Xem đáp án

Chọn đáp án B

Câu 7:

Cho tam giác ABC cân tại A có BC = 10cm . Gọi AD là tia phân giác của $\hat{B A C}$ . Tính CD?

A. 4

B. 3

C. 5

D. 2

Xem đáp án

Theo tính chất tia phân giác của góc ta có:

Do tam giác ABC cân tại A nên AB = AC nên:

Suy ra : DB = DC.

Mà DB + DC = BC nên:

Chọn đáp án C

Câu 8:

Cho tam giác ABC có AD là tia phân giác của góc BAC. Biết AB = 3cm, BD = 4cm, CD = 6cm. Tính AC?

A. 4cm

B. 5cm

C. 6cm

D. 4,5cm

Xem đáp án

Theo tính chất tia phân giác của góc ta có:

Suy ra:

Chọn đáp án D

Câu 9:

Cho tam giác ABC có đường trung tuyến AM và đường phân giác AD của góc BAC. Biết AB = 12 cm; AC = 8cm và BC = 15cm. Tính tỉ số BM/BD.

A. $\frac{5}{6}$

B. $\frac{7}{6}$

C. $\frac{1}{6}$

D. $\frac{3}{4}$

Xem đáp án

Do M là trung điểm của BC nên:

Vì AD là tia phân giác của góc BAC, theo tính chất tia phân giác của góc ta có:

Suy ra:

Theo tính chất của dãy tỉ số bằng nhau ta có:

Suy ra:

Do đó:

Chọn đáp án A

Câu 10:

Cho tam giác ABC có: AB = 4cm, AC = 5cm, BC = 6cm. Các đường phân giác BD và CE cắt nhau ở I. Tỉ số diện tích các tam giác DIE và ABC là:

A. $\frac{4}{55}$

B. $\frac{1}{8}$

C. $\frac{1}{10}$

D. $\frac{2}{45}$

Xem đáp án

Ta có: $\frac{A D}{A B} = \frac{D C}{B C}$ (t/c)

$\Rightarrow \frac{A D}{4} = \frac{D C}{6} = \frac{A D + D C}{4 + 6} = \frac{5}{10} = \frac{1}{2}$

=> AD = 4. $\frac{1}{2}$ = 2, DC = 6. $\frac{1}{2}$ = 3

Suy ra:

$\frac{D I}{I B} = \frac{D C}{C B} = \frac{3}{6} = \frac{1}{2} \Rightarrow \frac{D I}{D B} = \frac{1}{3} \frac{B E}{E A} = \frac{B C}{A C} = \frac{6}{5} \Rightarrow \frac{B E}{B A} = \frac{6}{11} \frac{A D}{D C} = \frac{2}{3} \Rightarrow \frac{A D}{A C} = \frac{2}{5}$

Suy ra $S_{D I E} = \frac{1}{3} S_{B D E}$

$\Rightarrow S_{D I E} = \frac{1}{3} . \frac{6}{11} . \frac{2}{5} = \frac{4}{55} S_{A B C}$

Vậy $\frac{S_{D I E}}{S_{A B C}} = \frac{4}{55}$

Đáp án: A

Câu 11:

Cho tam giác ABC, đường trung tuyến AM. Tia phân giác của góc AMB cắt AB ở D, tia phân giác của góc AMC cắt AC ở E. Gọi I là giao điểm của AM và DE. Chọn khẳng định đúng.

A. DE // BC

B. DI = IE

C. DI > IE

D. Cả A, B đều đúng

Xem đáp án

Vì MD và ME lần lượt là phân giác của $\hat{A M B}, \hat{A M C}$ nên $\frac{D A}{D B} = \frac{M A}{M B}, \frac{E A}{E C} = \frac{M A}{M C}$

Mà MB = MC nên $\frac{D A}{D B} = \frac{E A}{E C}$ => DE // BC (định lí Talet đảo)

Vì DE // BC nên $\frac{D I}{B M} = \frac{A I}{A M} = \frac{I E}{M C}$ (hệ quả định lí Talet) mà BM = MC nên DI = IE.

Nên cả A, B đều đúng.

Đáp án: D

Câu 12:

Cho tam giác ABC, đường trung tuyến AM. Tia phân giác của góc AMB cắt AB ở D, tia phân giác của góc AMC cắt AC ở E. Gọi I là giao điểm của AM và DE. Tính độ dài DE, biết BC = 30cm, AM = 10cm.

A. 9cm

B. 6cm

C. 15cm

D. 12cm

Xem đáp án

Vì DI = IE (cmt) nên MI là đường trung tuyến của tam giác MDE.

ΔMDE vuông (vì MD, ME là tia phân giác của góc kề bù) nên MI = DI = IE

Đặt DI = MI = x, ta có $\frac{D I}{B M} = \frac{A I}{A M}$ (cmt) nên $\frac{x}{15} = \frac{10 - x}{10}$

Từ đó x = 6 suy ra DE = 12cm

Đáp án: D

Câu 13:

Cho tam giác ABC có: AB = 12cm, BC = 15cm, AC = 18cm. Gọi I là giao điểm của các đường phân giác và G là trọng tâm tam giác. Biết D và M lần lượt là giao điểm của AI, AG với BC. Chọn khẳng định sai:

A. IG // BC

B. $\frac{A I}{I D} = \frac{A G}{G M}$

C. $\hat{A B G} = \hat{C B G}$

D. $\frac{I D}{A D} = \frac{M G}{M A}$

Xem đáp án

Gọi D, M là giao điểm của AI, AG với BC.

Vì AD là tia phân giác góc $\hat{B A C}$ nên $\frac{B D}{A B} = \frac{D C}{A C}$ (t/c)

$\Rightarrow \frac{B D}{12} = \frac{D C}{18} = \frac{B D + D C}{12 + 18} = \frac{15}{30} = \frac{1}{2}$

=> BD = 12. $\frac{1}{2}$ = 6, DC =18. $\frac{1}{2}$ = 9

Lại có: BI là tia phân giác $\hat{A B D}$ nên $\frac{A I}{I D} = \frac{A B}{B D} = \frac{12}{6} = 2$ (tính chất)

=> $\frac{I D}{A D} = \frac{M G}{M A} = \frac{1}{3}$ hay D đúng

Mà AG = 2GM (vì G là trọng tâm)

Nên $\frac{A I}{I D} = \frac{A G}{G M} = 2$ hay B đúng

Theo định lí đảo của định lí Talet ta có:

IG // DM => IG // BC hay A đúng

Chỉ có C sai

Đáp án: C

Câu 14:

Cho tam giác ABC có: AB = 12cm, BC = 15cm, AC = 18cm. Gọi I là giao điểm của các đường phân giác và G là trọng tâm tam giác. Độ dài IG là:

A. 1 cm

B. 2 cm

C. 1,5 cm

D. 2,5 cm

Xem đáp án

Do M là trung điểm BC nên MB = $\frac{1}{2}$ BC = $\frac{1}{2}$ .15 = 7,5 cm

Mà BD = 6cm nên DM = 7,5 cm – 6cm = 1,5 cm

Do IG // DM nên $\frac{I G}{D M} = \frac{A G}{A M} = \frac{2}{3}$ => IG = $\frac{2}{3}$ DM = $\frac{1}{3}$ .1,5 = 1 cm

Đáp án: A

Câu 15:

Cho tam giác ABC, AB = AC = 10cm, BC = 12cm. Gọi I là giao điểm của các đường phân giác của tam giác ABC. Độ dài AI là:

A. 9cm

B. 6cm

C. 5cm

D. $3 \sqrt{5}$ cm

Xem đáp án

Ta có: AB = AC = 10cm

Suy ra ΔABC cân tại A

Có I là giao các đường phân giác của ΔABC

Suy ra AI, BI là đường phân giác của ΔABC

Gọi H là giao của AI và BC

Khi đó ta có AH vừa là đường phân giác, vừa là đường cao, vừa là đường trung tuyến ứng với cạnh đáy của tam giác cân ABC (tính chất tam giác cân).

=> H là trung điểm của cạnh BC

=> BH = HC = $\frac{B C}{2} = \frac{12}{2}$ = 6cm

Áp dụng định lý Pitago trong tam giác ABH vuông tại H, ta có:

$A H^{2} + B H^{2} = A B^{2} \Leftrightarrow A H^{2} + 6^{2} = 10^{2} \Leftrightarrow A H^{2} = 100 - 36 = 64 \Rightarrow A H = 8$

Vì BI là phân giác của tam giác ABH nên: $\frac{A I}{I H} = \frac{A B}{B H} = \frac{10}{6} = \frac{5}{3}$

$\Leftrightarrow \frac{A I}{5} = \frac{I H}{3}$

Theo tính chất dãy tỉ số bằng nhau ta có:

$\frac{A I}{5} = \frac{I H}{3} = \frac{A I + I H}{5 + 3} = \frac{A H}{8} = \frac{8}{8} = 1$

=> AI = 5(cm)

Đáp án: C

Câu 16:

Cho tam giác ABC có chu vi 18cm, các đường phân giác BD và CE. Tính các cạnh của tam giác ABC, biết $\frac{A D}{D C} = \frac{1}{2}, \frac{A E}{E B} = \frac{3}{4}$

A. AC = 4cm, BC = 8cm, AB = 6cm

B. AB = 4cm, BC = 6cm, AC = 8cm

C. AB = 4cm, BC = 8cm, AC = 6cm

D. AB = 8cm, BC = 4cm, AC = 6cm

Xem đáp án

Theo tính chất đường phân giác, ta có: $\frac{A B}{B C} = \frac{A D}{D C} = \frac{1}{2}; \frac{A C}{B C} = \frac{A E}{E B} = \frac{3}{4}$

Nên $\frac{A B}{2} = \frac{B C}{4} = \frac{A C}{3}$

Do đó:

$\frac{A B}{2} = \frac{B C}{4} = \frac{A C}{3} = \frac{A B + B C + A C}{2 + 4 + 3} = \frac{18}{9} = 2$

Vậy AB = 4cm, BC = 8cm, AC = 6cm

Đáp án: C