15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 8 CTST Bài 1. Hình chóp tam giác đều - Hình chóp tứ giác đều có đáp án

Câu 1:

Mặt đáy của hình chóp tam giác đều là hình gì?

A. Tam giác vuông cân.

B. Tam giác cân.

C. Tam giác vuông.

D. Tam giác đều.

Xem đáp án

Lời giải

Đáp án đúng là: D

Theo định nghĩa hình chóp tam giác đều, mặt đáy là các tam giác đều.

Câu 2:

Hình chóp tứ giác đều có mấy cạnh bên?

A. 3.

B. 4.

C. 5.

D. 6.

Xem đáp án

Lời giải

Đáp án đúng là: B

Hình chóp tam giác đều có 4 cạnh bên.

Câu 3:

Đường cao của hình chóp tam giác đều trong hình bên là

A. SH.

B. SO.

C. AH.

D. AB.

Xem đáp án

Lời giải

Đáp án đúng là: B

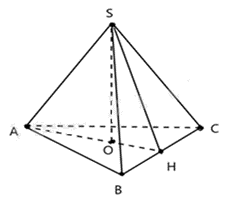
Theo khái niệm đường cao của hình chóp tam giác đều thì đường cao của hình chóp S.ABC là đoạn SO.

Câu 4:

Cho hình chóp tứ giác đều S.ABCD như hình. Gọi O là giao điểm hai đường chéo, khi đó SO là:

A. đường cao của hình chóp.

B. cạnh trong của hình chóp.

C. cạnh bên của hình chóp.

D. trung tuyến của hình chóp.

Xem đáp án

Lời giải

Đáp án đúng là: A

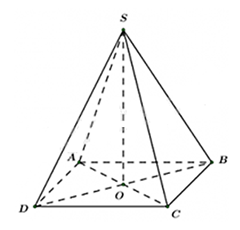
Theo định nghĩa đường cao của hình chóp tứ giác đều thì đường cao là đoạn thẳng nối từ đỉnh tới giao của hai đường chéo của mặt đáy.

Khi đó, SO là đường cao của hình chóp tứ giác đều S.ABCD.

Câu 5:

Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau và bằng 6 cm. Chu vi mặt đáy của hình chóp tứ giác đều S.ABCD

A. 18 cm

B. 6 cm

C. 24 cm

D. 36 cm

Xem đáp án

Lời giải

Đáp án đúng là: C

Hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông nên

AB = BC = CD = DA = 6 cm .

Khi đó chu vi mặt đáy ABCD là: C = 6.4 = 24 (cm).

Câu 6:

Hình chóp tam giác đều có mấy mặt?

A. 3.

B. 5.

C. 4.

D. 6.

Xem đáp án

Lời giải

Đáp án đúng là: C

Hình chóp tam giác có 4 mặt bao gồm 3 mặt bên và 1 mặt đáy.

Câu 7:

Cho hình chóp tam giác đều SABC như hình. Mặt đáy của hình chóp là

A. mặt SAB.

B. mặt SBC.

C. mặt SAC.

D. mặt ABC.

Xem đáp án

Lời giải

Đáp án đúng là: D

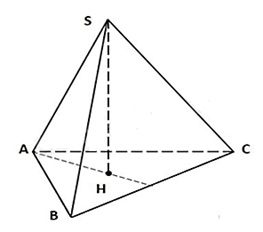
Theo định nghĩa hình chóp tam giác đều thì mặt đáy của hình chóp SABC là mặt ABC.

Câu 8:

Số đo mỗi góc ở đỉnh của mặt đáy hình chóp tam giác đều là

A. \(45^\circ \)

B. \(90^\circ \)

C. \(60^\circ \)

D. \(30^\circ \)

Xem đáp án

Lời giải

Đáp án đúng là: C

Vì đáy của hình chóp tam giác đều là tam giác đều, mà mỗi góc của tam giác đều có số đo bằng \(60^\circ \).

Câu 9:

Chọn phát biểu sai trong các phát biểu sau:

A.Hình chóp tam giác đều có tất cả các cạnh bên bằng nhau và đáy là tam giác đều.

B. Hình chóp tứ giác đều có tất cả các cạnh bằng nhau.

C. Hình chóp tứ giác đều có các cạnh bên bằng nhau và đáy là hình vuông.

D. Hình chóp tam giác đều có các mặt bên là tam giác cân.

Xem đáp án

Lời giải

Đáp án đúng là: B

Hình chóp tứ giác đều có các cạnh bên bằng nhau và đáy là hình vuông nên đáp án B sai.

Câu 10:

Cho hình chóp tam giác đều S.ABC, có SA = 4cm, AB = 5cm. So sánh độ dài cạnh SB và SC.

A. SB = SC.

B. SB > SC.

C. SB < SC.

D. Không so sánh được.

Xem đáp án

Lời giải

Đáp án đúng là: A

Hình chóp tam giác đều có các mặt bên là các tam giác cân bằng nhau có chung đỉnh nên SB = SC = SA = 4 cm.

Câu 11:

Bạn A định gấp một hộp quà từ tấm bìa như hình dưới. Bạn A định gấp hình gì?

A. Hình lập phương.

B. Hình chóp tam giác đều.

C. Hình lăng trụ.

D. Hình chóp tứ giác đều.

Xem đáp án

Lời giải

Đáp án đúng là: B

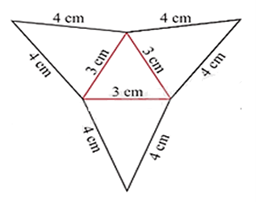
Sử dụng định nghĩa hình chóp tam giác đều, hình chóp tứ giác đều ta thấy các cạnh bên bằng nhau, đáy của hình trên là tam giác đều.

Câu 12:

Hình nào dưới đây khi gấp lại được hình chóp tam giác đều?

A. Hình b

B. Hình a

C. Hình c

D. Không có hình nào

Xem đáp án

Lời giải

Đáp án đúng là: B

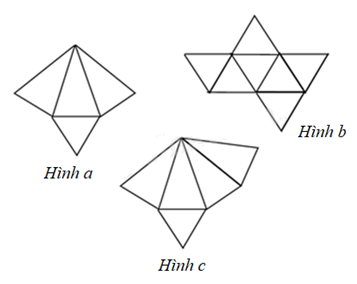
Hình 1: Khi gấp lại, ta gấp được hình chóp tam giác đều vì có ba mặt bên và đáy là tam giác đều.

Hình 2: Khi gấp lại, hình chóp không đều vì thừa nhiều mặt.

Hình 3: Khi gấp lại, không được hình chóp tam giác đều vì thừa một mặt.

Câu 13:

Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, nếu tăng cạnh bên lên hai lần thì chu vi mặt đáy sẽ

A. Giảm đi 2 lần

B. Tăng lên 2 lần

C. Giảm đi 4 lần.

D. Tăng lên 4 lần.

Xem đáp án

Lời giải

Đáp án đúng là: B

Hình chóp tứ giác đều có đáy là hình vuông, tất cả các cạnh đều bằng nhau nên cạnh bên tăng lên hai lần thì cạnh đáy tăng hai lần.

Khi đó, chu vi hình vuông cũng tăng lên 2 lần.

Câu 14:

Cho hình chóp tam giác đều S.ABC biết SA = 4 cm, AB = 3 cm. Chọn phát biểu đúng.

A. SC = AC = 3 cm.

B. AC = BC = 3 cm.

C. SB = BC = 4 cm.

D. SB = SC = 3 cm.

Xem đáp án

Lời giải

Đáp án đúng là: B

Hình chóp tam giác đều S.ABC có đáy ABC là tam giác đều nên

AC = BC = AB = 3 cm.

Hình chóp tam giác đều có các mặt bên là các tam giác cân bằng nhau có chung đỉnh nên SB = SC = SA = 4 cm.

Câu 15:

Cho hình chóp tam giác đều S.ABC có tất cả các cạnh bằng nhau, chiều cao mặt đáy bằng \[3\sqrt 3 \,\,{\rm{cm}}\]. Tính chiều cao mặt bên hình chóp.

A. \[3\sqrt 3 \,\,{\rm{cm}}\]

B. 3 cm

C. \[\frac{{3\sqrt 3 }}{2}\,\,{\rm{cm}}\]

D. \[\frac{3}{2}\,\,{\rm{cm}}\]

Xem đáp án

Lời giải

Đáp án đúng là: A

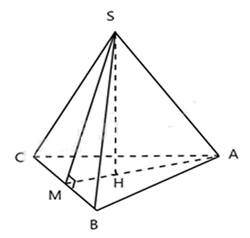
Hình chóp tam giác đều S.ABC có tất cả các cạnh bằng nhau nên

SA = SB = SC = AB = AC = BC.

Gọi H là trọng tâm tam giác ABC đều, M là trung điểm BC.

Theo định nghĩa trung đoạn, SM là trung đoạn của hình chóp.

Đáy ABC là tam giác đều nên AM vừa là trung tuyến vừa là đường cao

Suy ra \[{\rm{AM}} \bot {\rm{BC}} \Rightarrow \widehat {{\rm{AMB}}}{\rm{ = 90}}^\circ \Rightarrow {\rm{\Delta AMB}}\] vuông tại M.

\[{\rm{AM = 3}}\sqrt {\rm{3}} \,\,{\rm{cm}}\].

Ta có: SA = SB = SC nên tam giác SAB đều

Khi đó, SM vừa là trung tuyến vừa là đường cao.

\[ \Rightarrow {\rm{SM}} \bot {\rm{BC}} \Rightarrow \widehat {{\rm{SMB}}}{\rm{ = 90}}^\circ \Rightarrow {\rm{\Delta SMB}}\] vuông tại M.

Xét tam giác vuông SMB và tam giác vuông AMB có:

MB chung

SB = AB

Do đó \[{\rm{\Delta SMB = \Delta AMB}}\] (cạnh huyền – cạnh góc vuông)

Suy ra \[{\rm{SM = AM = 3}}\sqrt {\rm{3}} \,\,{\rm{(cm)}}\].

Vậy chiều cao mặt bên hình chóp SM bằng \[{\rm{3}}\sqrt {\rm{3}} \,\,{\rm{cm}}\].