4 câu hỏi trắc nghiệm thuộc Dạng 1. Nhận dạng hình vuông có đáp án

Bài tập Toán 8 Chủ đề 15: Hình vuông có đáp án

Dạng 1. Nhận dạng hình vuông có đáp án

975 lượt thi
4 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho hình 99, tứ giác AEDF là hình gì? Vì sao?

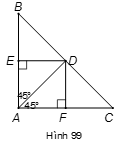
Xem đáp án

Theo hình vẽ thì $\hat{A} = \hat{E} = \hat{F} = 90^{0}$ . Tứ giác AEDF có ba góc vuông nên nó là hình chữ nhật. Hình chữ nhật AEDF có AD là đường phân giác của góc A nên nó là hình vuông.

Câu 2:

Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F lần lượt là trung điểm của AB và CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.

a) Tứ giác ADFE là hình gì? Vì sao?

Xem đáp án

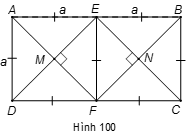
Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F lần lượt là trung điểm của AB và CD. a) Tứ giác ADFE là hình gì? Vì sao? (ảnh 1)

Đặt AD = a thì AB = 2a.

Áp dụng tính chất về cạnh và giả thiết vào hình chữ nhật ABCD, ta được AE = EB = BC = CF = FA = a.

a) Tứ giác ADFE là hình vuông.

Giải thích: Vì tứ giác ADFE có bốn cạnh bằng nhau nên nó là hình thoi.

Hình thoi ADFE có $\hat{A} = 90^{0}$ nên nó là hình vuông.

Câu 3:

b) Tứ giác MENF là hình gì? Vì sao?

Xem đáp án

b) Tứ giác MNEF là hình vuông.

Giải thích:

Chứng minh tương tự như câu a) ta cũng có tứ giác EBCF là hình vuông.

Áp dụng tính chất về đường chéo vào hai hình vuông ADFE và MENF, ta được:

$\{\begin{matrix} A F ⊥ D E; E C ⊥ F B \\ \hat{E_{1}} = \hat{E_{2}} = 45^{0} \end{matrix} \Rightarrow \hat{M} = \hat{N} = \hat{E} = 90^{0}$ .

Tứ giác MENF có ba góc vuông nên nó là hình chữ nhật.

Hình chữ nhật MENF lại có EF là đường phân giác của góc MEN nên nó là hình vuông.

Câu 4:

Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao cho AM = BN = CP = DQ. Chứng minh rằng tứ giác MNPQ là hình vuông.

Xem đáp án

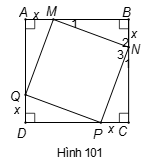
Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao cho AM = BN = CP = DQ. Chứng minh rằng tứ giác MNPQ là hình vuông. (ảnh 1)

Gọi độ dài cạnh hình vuông là a và $A M = B N = C P = D O = x$ .

Áp dụng định nghĩa và giả thiết vào hình vuông ABCD, ta được:

$\hat{A} = \hat{B} = \hat{C} = \hat{D} = 90^{0}$ và $M B = N C = P D = Q A = a - x$ , nên bốn tam giác vuông $M B N, N C P, P D Q, Q A M$ bằng nhau trường hợp (c-g-c) suy ra bốn cạnh tương ứng của các tam giác đó bằng nhau là $M N = N P = P Q = Q A$ . Tứ giác MNPQ có bốn cạnh bằng nhau nên nó là hình thoi.

Áp dụng tính chất về góc và kết quả hai tam giác bằng nhau vào hai tam giác MBN, NCP ta được:

$\{\begin{matrix} \hat{M_{1}} + \hat{N_{2}} = 90^{0} \\ \hat{M_{1}} = \hat{N_{1}} \end{matrix} \Rightarrow \hat{N_{1}} + \hat{N_{2}} = 90^{0}$ (1)

Lại có góc BNC là góc bẹt hay

$\hat{B N C} = \hat{N_{1}} + \hat{N_{2}} + \hat{N_{3}} = 180^{0}$ (2)

Từ (1) và (2) suy ra $\hat{N_{3}} = 180^{0} - 90^{0} = 90^{0}$ .

Điều này chứng tỏ hình thoi MNPQ có một góc vuông nên nó là hình vuông.

Bắt đầu thi ngay