Trắc nghiệm chuyên đề Toán 8 Chủ đề 6. Ôn tập và kiểm tra có đáp án
-
1516 lượt thi
-
47 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Chọn đáp án C.
Ta cần nhớ định nghĩa: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
Câu 2:
 Xem đáp án
Xem đáp án
Chọn đáp án A.
Ta cần nhớ định nghĩa: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
Lục giác đều là đa giác có 6 cạnh và 6 góc bằng nhau.Câu 3:
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?
A. Hình vuông là đa giác đều.
B. Tổng các góc của đa giác lồi 8 cạnh là 10800.
C. Hình thoi là đa giác đều.
D. Số đo góc của hình bát giác đều là 135,50.
 Xem đáp án
Xem đáp án
Ta cần nhớ định nghĩa: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
+ Hình vuông là hình có 4 cạnh bằng nhau và 4 góc bằng nhau
⇒ Hình vuông là đa giác đều.
⇒ Đáp án A đúng.
+ Hình thoi là hình có 4 cạnh bằng nhau nhưng 4 góc không bằng nhau.
⇒ Hình thoi không phải là đa giác đều.
⇒ Đáp án C sai.
+ Tổng số đo các góc của đa giác n cạnh là ( n - 2 ).1800.
Khi đó tổng các góc của đa giác lồi 8 cạnh là ( 8 - 2 ).1800 = 10800.
⇒ Đáp án B đúng.
+ Số đo của một góc của đa giác đều n cạnh là
Khi đó số đo của hình bát giác đều là = 1350.
⇒ Đáp án D sai.
Câu 4:
 Xem đáp án
Xem đáp án
Chọn đáp án C.
Số đường chéo của đa giác n cạnh là
Khi đó số đường chéo của đa giác 7 cạnh là = 14 (đường chéo)
Câu 5:
 Xem đáp án
Xem đáp án
Chọn đáp án A.
Số đường chéo của đa giác n cạnh là . ( n ∈ N, n ≥ 3 )
Theo giả thiết ta có = n ⇔ n( n - 3 ) = 2n ⇔ n2 - 3n - 2n = 0
⇔ n2 - 5n = 0 ⇔ n( n - 5 ) = 0 ⇔
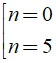
So sánh điều kiện ta có n = 5 thỏa mãn.
Câu 6:
 Xem đáp án
Xem đáp án
Chọn đáp án C.
Công thức diện tích hình chữ nhật là Shcn = a.b
Trong đó : a là chiều dài, b là chiều rộng
Theo giả thiết: Sban đầu = a.b
Khi đó ta có: Ssau = 4b..a = 2a.b = 2Sban đầu
Do đó, diện tích sau tăng lên 2 lần.
Câu 7:
 Xem đáp án
Xem đáp án
Chọn đáp án B.
Công thức diện tích hình chữ nhật là Shcn = a.b
Trong đó : a là chiều dài, b là chiều rộng
Khi đó ta có: Shcn = 4. 1,5 = 6( cm2 ).
Câu 8:
 Xem đáp án
Xem đáp án
Chọn đáp án D.
Diện tích hình vuông bằng bình phương cạnh của nó: S = a2.
Khi đó ta có Shv = 4.4 = 16 ( cm2 ).
Câu 9:
 Xem đáp án
Xem đáp án
Chọn đáp án C.
Diện tích tam giác vuông bằng nửa tích hai cạnh: S = .a.b.
Khi đó ta có S = . 6. 4 = 12( cm2 ).
Câu 10:
 Xem đáp án
Xem đáp án
Chọn đáp án B.
Diện tích hình vuông bằng bình phương cạnh của nó: S = a2.
Ngoài công thức này, diện tích hình vuông còn một công thức mở rộng là:
Diện tích hình vuông bằng nửa tích của hai đường chéo
Khi đó ta có : S = . 6. 6 = 18( cm2 ).
Câu 11:
Tam giác có độ dài cạnh đáy bằng a , độ dài cạnh huyền là h. Khi đó diện tích tam giác được tính bằng công thức ?
 Xem đáp án
Xem đáp án
Chọn đáp án C.
Ta có diện tích của tam giác: S = .a.h.
Trong đó: a là độ dài cạnh đáy, h là độ dài đường cao
Câu 12:
Diện tích tam giác SAHB = ? với H là chân đường cao kẻ từ A.
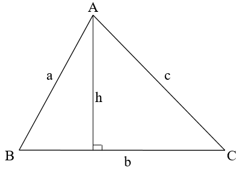
 Xem đáp án
Xem đáp án
Chọn đáp án C.
Ta có: SAHB + SAHC = SABC ⇒ SAHB = SABC - SAHC
Câu 13:
 Xem đáp án
Xem đáp án
Chọn đáp án C.
Ta có diện tích của tam giác: S = b.h.
Trong đó: b là độ dài cạnh đáy, h là độ dài đường cao
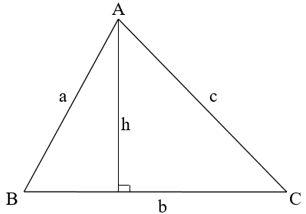
Khi đó ta có :
S = .AH.BC = .BC.BC = .BC2.
Câu 14:
 Xem đáp án
Xem đáp án
Chọn đáp án B.
Ta có diện tích Δ ABC là S = AH.BC = .6.4 = 12( cm2 ).
Câu 15:
 Xem đáp án
Xem đáp án
Chọn đáp án C.
Áp dụng định lý Py – ta – go ta có AB2 + AC2 = BC2 ⇒ AC = √ (BC2 - AB2)
⇒ AC = √ (52 - 42) = 3cm.
Khi đó SABC = AB.AC = 1/2.4.3 = 6( cm2 )
Câu 16:
 Xem đáp án
Xem đáp án
Chọn đáp án A.
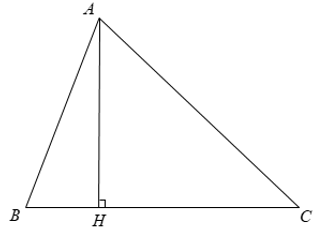
Áp dụng định lý Py – ta – go ta có:
+ Xét Δ ABH có AH2 + BH2 = AB2 ⇒ AH = √ (AB2 - BH2)
⇒ AH = √ (152 - 122) = 9 ( cm ).
+ Xét Δ ACH có AC2 = AH2 + HC2 ⇒ HC = √ (AC2 - AH2)
⇒ HC = √ (412 - 92) = 40 ( cm ).
Khi đó SABC = AH.BC = AH( HB + HC ) = .9.( 12 + 40 ) = 234 ( cm2 ).
Câu 17:
 Xem đáp án
Xem đáp án
Chọn đáp án B.
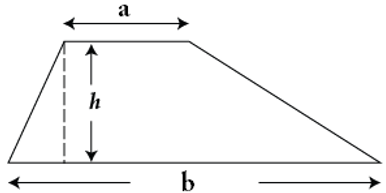
Ta có: S = ( a + b ).h
Khi đó ta có:
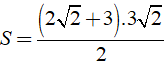
= 3√ 2 .( √ 2 + 3/2 ) = 3( 2 +)cm2
Câu 18:
Hình thang có độ dài đáy lần lượt là 6cm, 4cm và diện tích hình thang đó là 15cm2. Chiều cao hình thang có độ dài là ?
 Xem đáp án
Xem đáp án
Chọn đáp án A.
Diện tích của hình thang là S = ( a + b ).h
⇒ ( a + b ).h = 2S ⇔ h = .
Khi đó, chiều cao của hình thang là h = = 3( cm ).
Câu 19:
 Xem đáp án
Xem đáp án
Chọn đáp án B.
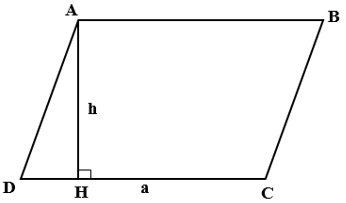
Ta có : S = a.h
Khi đó ta có: S = 4.2 = 8( cm2 ).
Câu 20:
 Xem đáp án
Xem đáp án
Chọn đáp án D.
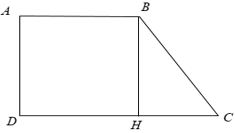
Xét hình thang ABCD
Từ B kẻ BH ⊥ CD, khi đó ta được hình chữ nhật ABHD ⇒ AB = DH = 2cm
⇒ HC = CD - DH = 4 - 2 = 2cm.
+ Xét Δ BDC có BH là đường cao đồng thời là đường trung tuyến
⇒ Δ BDC là tam giác cân tại B.
Mà BCDˆ = 450 ⇒ BDCˆ = 450
⇒ DˆBC = 1800 - ( BCDˆ + BDCˆ ) = 1800 - 900 = 900.
⇒ Δ BDC là tam giác vuông cân tại B nên BH = DC = 2cm.
Do đó 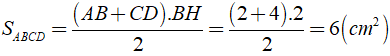
Câu 21:
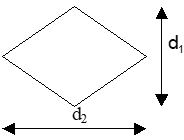
Công thức diện tích hình thoi là ?
 Xem đáp án
Xem đáp án
Chọn đáp án B.
Diện tích của hình thoi là S = d1.d2
Trong đó d1,d2 lần lượt là độ dài hai đường chéo.
Câu 22:
 Xem đáp án
Xem đáp án
Chọn đáp án B.
Diện tích của hình thoi là S = d1.d2
Trong đó d1,d2 lần lượt là độ dài hai đường chéo.
Khi đó, diện tích của hình thoi là Shình thoi = .8.10 = 40( cm2 )
Câu 23:
Hình thoi có độ dài hai đường chéo lần lượt là a√ 2 ,cm, a√ 3 cm. Diện tích của hình thoi là ?
 Xem đáp án
Xem đáp án
Chọn đáp án C.
Diện tích của hình thoi là S = d1.d2
Trong đó d1,d2 lần lượt là độ dài hai đường chéo.
Khi đó, diện tích của hình thoi là Shình thoi = . a√ 2 . a√ 3 = ( cm2 )
Câu 24:
 Xem đáp án
Xem đáp án
Chọn đáp án B.
Xét hình thoi ABCD có BACˆ = 600.
Ta có
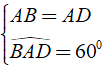
⇒ Δ ABD đều
⇒ AB = AD = BD = 4cm
Gọi H là giao điểm của hai đường chéo AC,BD.
Áp dụng định lí Py – ta – go ta có:
AH2 + HB2 = AB2 ⇒ AH = √ (AB2 - HB2)
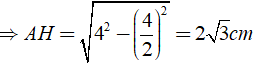
⇒ AC = 2AH = 4√ 3 ( cm )
Do đó SABCD = AC.BD = .4√ 3 .4 = 8√ 3 ( cm2 )
Câu 25:
 Xem đáp án
Xem đáp án
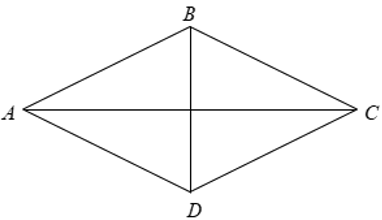
Gọi H là giao điểm của hai đường chéo AC,BD.
⇒ HB = HD = 4( cm )
Theo giải thiết ta có:
PABCD = AB + BC + CD + DA = 40
⇒ AB = BC = CD = DA = 10( cm )
Áp dụng định lý Py – ta – go ta có :
AH2 + HB2 = AB2 ⇒ AH = √ (AB2 - HB2) = √ (102 - 42) = 2√ 21 ( cm )
⇒ AC = 2AH = 4√ 21 ( cm )
Do đó SABCD = .BD.AC = .4√ 21 .8 = 16√ 21 ( cm2 )
Câu 26:
Cho đa giác đều có 14 cạnh. Tính :
a) Tổng số đo góc của đa giác đó
 Xem đáp án
Xem đáp án
a) Tổng số đo các góc của đa giác n cạnh là ( n - 2 ).1800.
Tổng số đo của đa giác 14 cạnh là ( 14 - 2 ).1800 = 21600.
Câu 27:
b) Số đo một góc của đa giác
 Xem đáp án
Xem đáp án
b) Số đo của một góc của đa giác đều n cạnh là 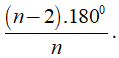
Số đo một góc của đa giác 14 cạnh là 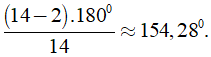
Câu 28:
c) Số đường chéo của đa giác.
 Xem đáp án
Xem đáp án
c) Số đường chéo của đa giác n cạnh là 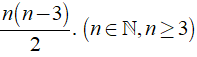
Số đường chéo của đa giác 14 cạnh là 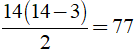 đường chéo
đường chéo
Câu 29:
Diện tích hình chữ nhật thay đổi như thế nào nếu :
a) Chiều dài tăng hai lần, chiều rộng không đổi
 Xem đáp án
Xem đáp án
Gọi chiều dài và chiều rộng của một hình chữ nhật lần lượt là a,b
Diện tích hình chữ nhật là Shcn = a.b.
a) Nếu chiều dài tăng lên 2 lần, chiều rộng không đổi thì khi đó chiều dài, chiều rộng mới là là 2a và b
Diện tích hình chữ nhật mới là Sm = 2a.b = 2S.
⇒ Diện tích hình chữ nhật tăng lên 2 lần.
Câu 30:
b) Chiều dài và chiều rộng tăng 3 lần.
 Xem đáp án
Xem đáp án
b) Nếu chiều dài và chiều rộng tăng lên 3 lần thì chiều dài, chiều rộng mới là 3a,3b
Diện tích hình chữ nhật mới là Sm = 3a.3b = 9S.
⇒ Diện tích hình chữ nhật tăng lên 9 lần.
Câu 31:
c) Chiều dài tăng 4 lần, chiều rộng giảm 4 lần.
 Xem đáp án
Xem đáp án
c) Nếu chiều dài tăng 4 lần, chiều rộng giảm đi 4 lần thì chiều dài, chiều rộng mới là 4a, b
Diện tích hình chữ nhật mới là Sm = 4a. b = ab = S.
⇒ Diện tích hình chữ nhật không đổi.
Câu 32:
Tính độ dài các cạnh hình chữ nhật biết rằng
a) Bình phương độ dài một cạnh là 16cm và diện tích hình chữ nhật là 28cm2.
 Xem đáp án
Xem đáp án
Gọi hai kích thước của hình chữ nhật là a,b ( a > 0, b > 0 ). Khi đó diện tích của hình chữ nhật là Shcn = a.b
a) Theo bài ra ta có: x.y = 28 ( 1 ) và x2 = 16 = 42 ⇔ x = 4 (vì x > 0 ), trường hợp y2 = 16 tương tự.
Thay x = 4 vào đẳng thức ( 1 ) ta có: 4y = 28 ⇔ y = 7.
Với x = 4, y = 7 thỏa mãn yêu cầu điều kiện.
Vậy hai kích thức của hình chữ nhật là 4cm, 7cm
Câu 33:
b) Tỉ số các cạnh là 4:9 và diện tích của nó là 144cm2.
 Xem đáp án
Xem đáp án
b) Theo bài ra ta có ( 2 ) và x.y = 144 ( 3 )
Nhân theo vế đẳng thức ( 2 ) với ( 3 ) ta được x2 = 82 ⇔ x = 8 (vì x > 0 )
Thay x = 8 vào đẳng thức ( 3 ) ta được 8y = 144 ⇔ y = 18.
Với x = 8, y = 18 thỏa mãn yêu cầu bài toán.
Vậy kích thức của hình chữ nhật là 8cm, 18cm.
Câu 34:
 Xem đáp án
Xem đáp án
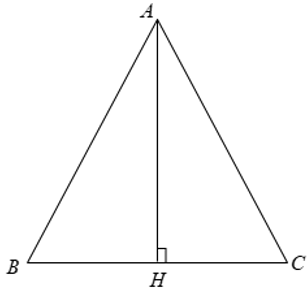
Xét Δ ABC cân tại A có AB = AC = b, BC = a.
Từ A kẻ AH ⊥ BC.
Ta có BH = HC = BC =
Khi đó ta có: SABC = AH.BC = .a.AH
Áp dụng định lý Py – to – go ta có:
AC2 = AH2 + HC2 ⇒ AH = √ (AC2 - HC2) .
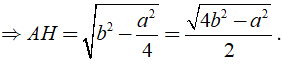
Khi đó SABC = AH.BC
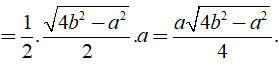
Do đó diện tích của tam giác đều các cạnh bằng a là
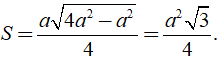
Câu 35:
 Xem đáp án
Xem đáp án
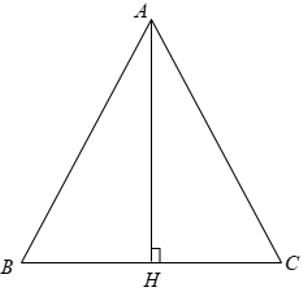
Xét Δ ABC cân tại A có BC = 30( cm )
⇒ BH = CH = 15( cm ).
Áp dụng đinh lý Py – ta – go ta có:
AB = √ (AH2 + HB2) = √ (202 + 152) = 25( cm )
Kẻ BK ⊥ AC, giờ ta phải tính BK = ?
Ta có : SABC = .AH.BC = .20.30 = 300 ( cm2 )
Mặt khác SABC = BK.AC = .BK.25
Do đó, ta có .BK.25 = 300 ⇔ BK = = 24( cm ).
Câu 36:
 Xem đáp án
Xem đáp án
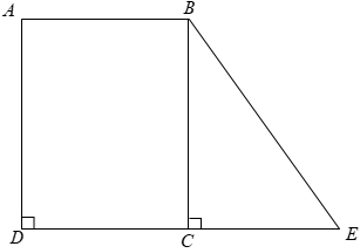
Theo bài ra ta có SABCD = AB.BC = 23.BC = 828 ⇒ BC = 36 ( cm )
Khi đó ta có 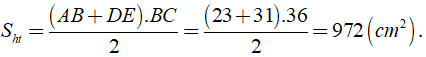
Vậy diện tích hình thang ABED là 972( cm2 )
Câu 37:
 Xem đáp án
Xem đáp án
Công thức diện tích của hình thoi là S = .d1.d2
Trong đó d1,d2 là độ dài của hai đường chéo.
Khi đó diện tích hình thoi cần tìm là: S = .10.12 = 60( cm2 )
Vậy diện tích hình thoi cần tìm là 60( cm2 )
Câu 38:
 Xem đáp án
Xem đáp án
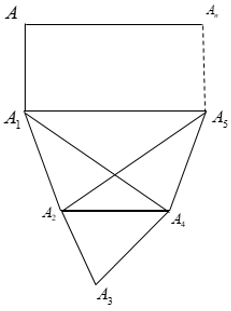
Nhận thấy: Hình vuông và hình ngũ giác đều thỏa mãn yêu cầu của bài toán
Ta chứng minh đa giác có số cạnh lớn hơn 5 không thỏa mãn yêu cầu của bài toán bằng phương pháp phản chứng.
Giả sử tồn tại đa giác AA1A2 ... An với n ≥ 6 có các đường chéo có độ dài bằng nhau.
⇒ A1A4 = A2A5 vì chúng là các đường chéo.
Xét tứ giác A1A2A4A5, có các đoạn thẳng A1A4,A2A5 là các đường chéo; còn A1A5,A2A4 là các cạnh của tứ giác nên tổng hai đường chéo lớn hơn tổng hai cạnh đối.
Hay A1A5 + A2A4 < A1A4 + A2A5 mẫu thuẫn với giải thiết quy nạp vì A1A5,A2A4 cũng là hai đường chéo của đa giác.
⇒ Giả thiết đưa ra là sai.
Vậy đa giác có số cạnh lớn hơn 5 thì không thỏa mãn yêu cầu bài.
Câu 39:
 Xem đáp án
Xem đáp án
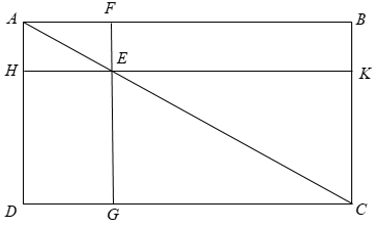
Theo giả thiết ta có FG//AD, HK//AB nên HE//AF và AH//EF.
Xét tứ giác AFEH có:
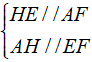
⇒ AFEH là hình bình hành.
Mà Aˆ = 900 ⇒ AFEH là hình chữ nhật.
⇒ Δ AFE = Δ AHE ( c - g - c ) → SAFE = SAHE.
Tương tự: SEKC = SEGC; SABC = SADC
⇒ SABC - SAFE - SEKC = SADC - SAHE - SEGC hay SEFBK = SEHDG.
Câu 40:
Trung tuyến AD và BE của Δ ABC cắt nhau tại G. Chứng minh rằng:
SDEG = SCEG = SCED = SABG = SABE = SABC.
 Xem đáp án
Xem đáp án
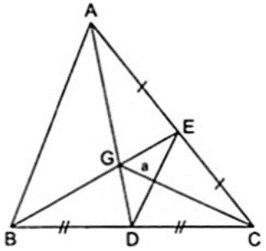
Đặt SDEG = a. Ta cần chứng minh:
SCEG = 2a; SCED = 3a; SABG = 4a; SABE = 6a; SABC = 12a
Đường trung tuyến AD và BE cứt nhau tại G nên G là trọng tâm của Δ ABC
⇒ Khoảng cách từ G đến các đỉnh của tam giác bằng độ dài các đường trung tuyến tương ứng.
Ta có SBDG = 2SDGE = 2a (vì chung đường cao kẻ từ D xuống BE và BG = 2GE )
SBDG = SCGD = 2a (vì chung đường cao kẻ từ G xuống BC và BD = DC )
Do đó SBDC = SBDG + SCGD = 2a + 2a = 4a.
Lại có SCEG = SBGC = .4a = 2a (vì chung đường cao kẻ từ C xuống BE và BG = 2GE )
+ SEDC = SEBD = 2a + a = 3a (vì chung đường cao kẻ từ E xuống BC và BD = DC )
+ SAGB = 2SGBD = 4a (vì chung đường cao kẻ từ B xuống AD và AG = 2GD )
+ SAEB = SAGB = .4a = 6a (vì chung đường cao kẻ từ A xuống BE và BE = BG )
+ SABC = 2SABE = 2.6a = 12a.
Câu 41:
 Xem đáp án
Xem đáp án
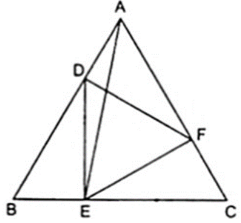
Đặt SABC = 9a. Ta có:
+ SABE = SABC = .9a = 3a (vì chung đường cao kẻ từ A xuống BC và BC = 3BE)
+ SADE = SABE = .3a = a (vì chung đường cao kẻ từ E xuống AB và AB = 3AD )
Do đó SBDE = SABE - SADE = 3a - a = 2a.
Tương tự: SADF = SCEF = 2a
Vậy SDEF = 9a - 6a = 3a hay SABC = 3SDEF.
Câu 42:
Cho tam giác nhọn ABC, các đường cao AA', BB', CC' cắt nhau tại H. Chứng minh rằng: 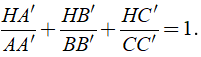
 Xem đáp án
Xem đáp án
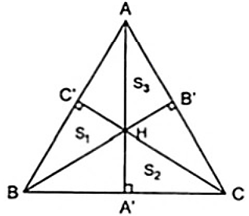
Gọi diện tích ABC, ABH,BCH,CAH lần lượt là S,S1,S2,S3.
Ta có S = S1 + S2 + S3.
+ Các tam giác ABC và ABH có chung đáy AB nên tỉ số đường cao bằng tỉ số diện tích: 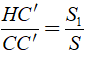
+ Tương tự: 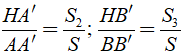
Khi đó ta có 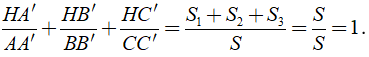
Câu 43:
Chứng minh rằng 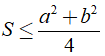 với S là diện tích của tam giác có độ dài hai cạnh là a,b ?
với S là diện tích của tam giác có độ dài hai cạnh là a,b ?
 Xem đáp án
Xem đáp án
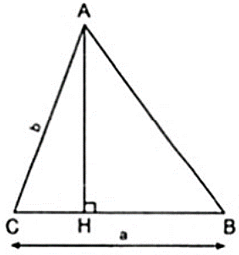
Xét tam giác ABC có BC = a, AC = b
Kẻ AH ⊥ BC thì AH và AC lần lượt là đường xiên.
Đường vuông góc kẻ từ A ở ngoài đường thẳng BC đến đường thẳng đó nên đường AH là đường ngắn nhất hay AH ≤ AC.
Khi đó ta có: 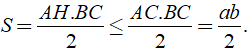
Mặt khác ta có:
+ 4ab = ( a + b )2 - ( a - b )2 ≤ ( a + b )2 ( 1 )
+ 2( a2 + b2 ) = ( a + b )2 + ( a - b )2 ≥ ( a + b )2 ( 2 )
Từ ( 1 ) và ( 2 ), ta có: 4ab ≤ 2( a2 + b2 ) ⇒ 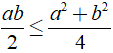
Hay 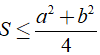 (đpcm)
(đpcm)
Câu 44:
 Xem đáp án
Xem đáp án
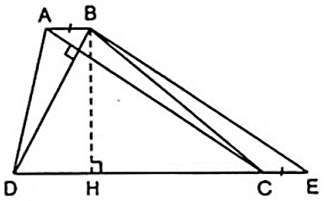
Xét hình thang ABCD ( AB//CD ) có AC ⊥ BD và AC = 6dm, BD = 3,6dm.
Kẻ đường cao BH của hình thang.
Ta có 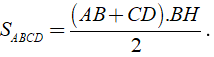
Kẻ BE//AC thì BD ⊥ BE thì hình thang ABEC có hai cặp cạnh đối song song → ABEC là hình bình hành.
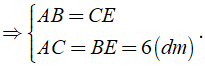
Do đó, ta có: CD + AB = CD + CE = DE
Khi đó ta có 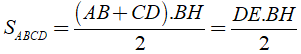
⇒ S là diện tích của tam giác DBE vuông tại B.
Khi đó S = BD.BE = .3,6. 6 = 10,8( dm2 )
Vậy diện tích của hình thang là 10,8( dm2 )
Câu 45:
 Xem đáp án
Xem đáp án
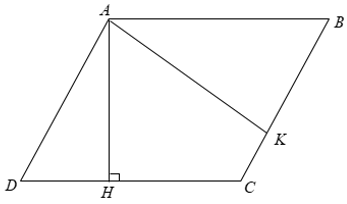
Xét hình bình bình ABCD có AB = CD = 8( cm ) và AD = BC = 6( cm )
Từ A kẻ các đường cao AH,AK.
Khi đó ta có:
+ Shbh = AH.CD = 8.AH
+ Shbh = AK.BC = 6.AK
Mà một hình bình hành thì chỉ có một diện tích chung nên 8.AH = 6.AK
Nếu độ dài đường cao thứ nhất là AH = 5( cm ) thì:
8.5 = 6.AK ⇔ AK = = ( cm ) là độ dài đường cao thứ hai.
Nếu độ dài đường cao thứ nhất là AK = 5( cm ) thì:
8.AH = 6.5 ⇔ AH = = ( cm ) là độ dài đường cao thứ hai.
Vậy bài toán này có hai đáp số
Câu 46:
 Xem đáp án
Xem đáp án
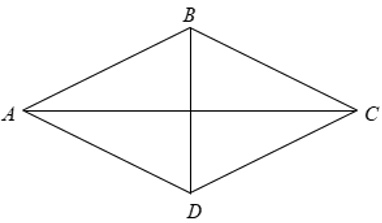
Gọi H là giao điểm của hai đường chéo AC,BD.
Theo giải thiết ta có: AC + BD = 46( cm )
⇔ ( HB + HD ) + ( HC + HA ) = 46
⇔ 2HB + 2HA = 46 ⇔ HA + HB = 23
Khi đó ta có: HA + HB = 23 ⇔ ( HA + HB )2 = 232
⇔ HA2 + 2HA.HB + HB2 = 232 ( 1 )
Mặt khác, theo định lí Py – to – go ta có: AH2 + HB2 = AB2 = 172 ( 2 )
Từ ( 1 ) và ( 2 ) ta có: 172 + 2HA.HB = 232 ⇒ HA.HB = = 120.
Hay = 120 ⇔ .AC.BD = 240 ⇒ SABCD = 240( cm2 )
Vậy diện tích hình thoi là 240cm2.
Câu 47:
 Xem đáp án
Xem đáp án
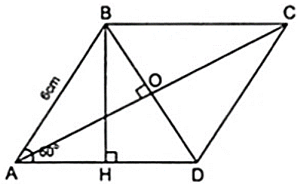
Diện tích của hình thoi ABCD là S = AC.BD
Gọi O là giao điểm của AC và BD
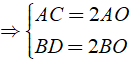
⇒ S = 2OA.OB
Từ giả thiết ta có hình thoi ABCD có Aˆ = 600 nên Δ ABD đều
Do đó Δ ABO là nửa tam giác đều có BO = BD = = 3( cm ).
Áo dụng định lí Py – to – go ta có:
AB2 = AO2 + BO2 ⇒ AO = √ (AB2 - BO2) = √ (62 - 32) = 3√ 3 ( cm )
Khi đó ta có: S = 2OA.OB = 2.3√ 3 .3 = 18√ 3 ( cm2 )
Vậy diện tích hình thoi là 18√ 3 ( cm2 )
