Trắc nghiệm chuyên đề Toán 8 Chủ đề 1: Tứ giác có đáp án
-
1159 lượt thi
-
13 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho tứ giác ABCD có = 700, = 900. Các tia phân giác của các góc C và D cắt nhau tại O. Tính số đo góc CODˆ ?
 Xem đáp án
Xem đáp án
Áp dụng định lí: Tổng các góc của một tứ giác bằng 3600.
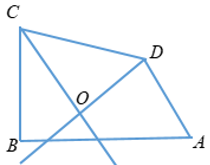
Ta có = 3600 ⇒ = 3600 - ( ) = 3600 - ( 700 + 900 )
⇒ = 2000
Theo giả thiết, ta có OC, OD là các đường phân giác
Khi đó ta có
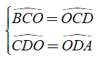
⇒ = =
⇔ 2() = 2000 ⇔ = 1000
Xét Δ OCD có = 1800 ⇒ = 1800 - () = 1800 - 1000 = 800.
Vậy = 800.
Câu 2:
 Xem đáp án
Xem đáp án
Khi đó ta có = 3600 ⇒ () = 3600 - () = 3600 - 1400 = 2200
Câu 3:
 Xem đáp án
Xem đáp án
Định lí: Tổng các góc của một tứ giác bằng 3600.
Theo giải thiết ta có A:B:C:D = 4:3:2:1 ⇒
Khi đó ta có = 3600 ⇔ = 3600
⇔ 10= 3600 ⇔ = 360.
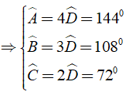
Câu 4:
 Xem đáp án
Xem đáp án
Chọn đáp án D.
Theo định lí: Tổng các góc của một tứ giác bằng 3600.
Nhận xét:
+ α là góc nhọn thì 0 < α < 900 ⇒ 0 < 4.α < 3600.
⇒ Không tồn tại tứ giác ABCD có 4 góc đều nhọn. ⇒ Loại A.
+ α là góc tù thì 900 < α < 1800 ⇒ 3600 < 4.α < 7200
⇒ Không tồn tại tứ giác ABCD có 4 góc đều tù. ⇒ Loại B.
+ α là góc vuông thì α = 900; β là góc tù thì 900 < β < 1800 ⇒ 1800 < 2.β < 3600
Khi đó ta có : 1800 + 1800 < 2α + 2β < 1800 + 3600
⇒ 3600 < 2α + 2β < 5400
⇒ Không tồn tại tứ giác ABCD có 2 góc nhọn và 2 góc tù. ⇒ Loại C.
+ Vì tứ giác có 4 góc vuông thì tổng các góc bằng 3600.
Câu 5:
 Xem đáp án
Xem đáp án
Chọn đáp án B.
Định lí: Tổng các góc của một tứ giác bằng 3600.
Khi đó ta có = 3600 ⇒ = 3600 - () = 3600 - ( 650 + 1170 + 710 )
⇒ = 3600 - 2530 = 1070.
Câu 6:
 Xem đáp án
Xem đáp án
Định lí: Tổng các góc của một tứ giác bằng 3600.
Khi đó ta có = 3600 ⇒ () = 3600 - () = 3600 - 1950 = 1650
Câu 7:
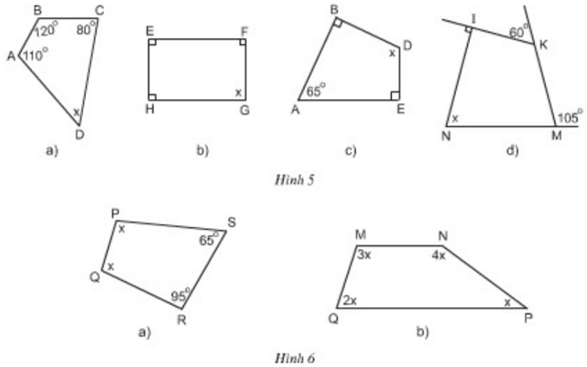
Tìm x ở hình 5, hình 6:
 Xem đáp án
Xem đáp án
(Áp dụng: tổng 4 góc trong một tứ giác bằng 360o)
- Ở hình 5:
a) x = 360o - (110o + 120o + 80o) = 50o
b) x = 360o - (90o + 90o + 90o) = 90o
c) x = 360o - (90o + 90o + 65o) = 115o
d) x = 360o - (75o + 120o + 90o) = 75o
Vì (kề bù với góc 60o)
∠M=180∘−105∘=75∘∠M=180∘−105∘=75∘(kề bù với góc 105o)
- Ở hình 6:
a) x + x = 360o - (65o + 95o) => x = 100o
b) 2x + 3x + 4x + x = 360o
=> 10x = 360o
=> x = 36o
Câu 8:
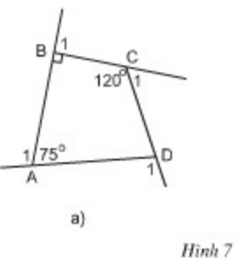
Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác.
Tính các góc ngoài của tứ giác ở hình 7a.
 Xem đáp án
Xem đáp án
Ở hình 7a: Góc trong còn lại:
∠D=360o−(75o+90o+120o)=75o∠D=360o−(75o+90o+120o)=75o
Ta tính được các góc ngoài tại các đỉnh A, B, C, D lần lượt là 105o, 90o, 60o, 105o
Câu 9:
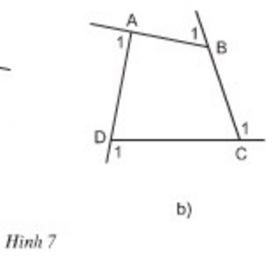
Tính tổng các góc ngoài của tứ giác ở hình 7b ( tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài):
 Xem đáp án
Xem đáp án
Tổng các góc trong:
∠A+∠B+∠C+∠D=360∘∠A+∠B+∠C+∠D=360∘
Nên tổng các góc ngoài:
∠A1+∠B1+∠C1+∠D1∠A1+∠B1+∠C1+∠D1
=(180∘−∠A)+(180∘−∠B)+(180∘−∠C)+(180∘−∠D)=(180∘−∠A)+(180∘−∠B)+(180∘−∠C)+(180∘−∠D)
=180∘.4−(∠A+∠B+∠C+∠D)=720∘−360∘=360∘=180∘.4−(∠A+∠B+∠C+∠D)=720∘−360∘=360∘
Câu 10:
 Xem đáp án
Xem đáp án
Nhận xét: Tổng các góc ngoài của tứ giác bằng 360o.
Câu 11:
Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình "cái diều". Tính ∠B, ∠D biết rằng ∠A= 1000 và ∠C= 600 .
 Xem đáp án
Xem đáp án
Xét ΔABC và ΔADC có:
AB = AD (gt)
BC = DC (gt)
AC cạnh chung
=> ΔABC = ΔADC (c.c.c)
Suy ra: ∠B=∠D∠B=∠D
Ta có: ∠B+∠D=360∘−(100∘+60∘)=200∘∠B+∠D=360∘−(100∘+60∘)=200∘
Do đó: ∠B=∠D=100∘∠B=∠D=100∘
Câu 12:
 Xem đáp án
Xem đáp án
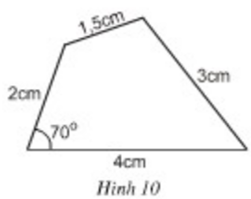
- Cách vẽ hình 10: Vẽ tam giác MQP trước rồi vẽ tam giác MNP. Vẽ tam giác MQP biết hai cạnh và góc xen giữa.
- Vẽ ∠xQy=70∘∠xQy=70∘
+ Trên tia Qx lấy điểm M sao cho QM = 2cm.
+ Trên tia Qy lấy điểm P sao cho QP = 4cm.
+ Vẽ đoạn thẳng MP, ta được tam giác MPQ.
Vẽ tam giác MNP biết ba cạnh, với cạnh MP đã vẽ. Tương tự cách vẽ hình 10, điểm N là giao điểm của hai cung tròn tâm M, P bán kính lần lượt là 1,5cm; 3cm.. Tứ giác MNPQ là tứ giác cần vẽ.
(*) Cách vẽ hình 10:
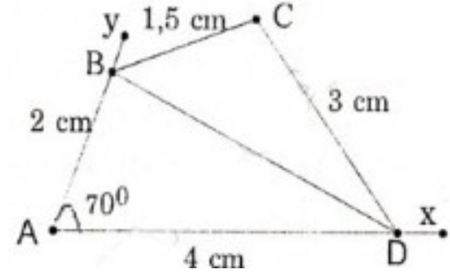
Câu 13:
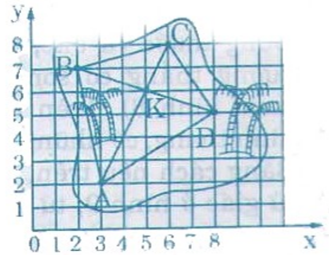
Đố em tìm thấy vị trí của "kho báu" trên hình 11, biết rằng kho báu nằm tại giao điểm các đường chéo của tứ giác ABCD, trong đó các đỉnh của tứ giác có tọa độ như sau: A(3; 2), B(2; 7), C(6; 8), D(8; 5).
 Xem đáp án
Xem đáp án
Các bước làm như sau:
Đánh dấu các số thứ tự (như trục tọa độ) và kí hiệu các điểm như trên hình. Các bước làm như sau:
- Xác định các điểm A, B, C, D trên hình vẽ với A(3; 2); B(2; 7); C(6; 8); D(8; 5).
- Vẽ tứ giác ABCD
- Vẽ hai đường chéo AC và BD. Gọi K là giao điểm của hai đường chéo đó.
- Xác định tọa độ của điểm K: K(5; 6)
Vậy vị trí kho báu có tọa độ K(5; 6) trên hình vẽ.