Đề kiểm tra Cuối kì 2 Toán 8 KNTT có đáp án (Đề 1)
-
682 lượt thi
-
18 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Sử dụng quy tắc đổi dấu, ta đưa phân thức về dạng phân thức nào sau đây?
 Xem đáp án
Xem đáp án
Chọn đáp án D
Câu 4:
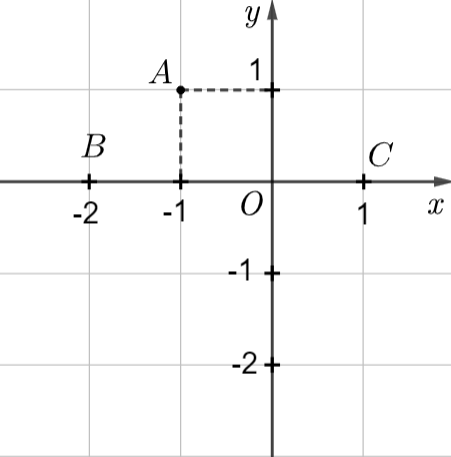
Trong mặt phẳng tọa độ Oxy cho các điểm như trong hình vẽ.
Điểm nào là điểm có tọa độ (-2;0)?
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 5:
Trong mặt phẳng tọa độ Oxy cho các điểm như trong hình vẽ.
Điểm nào là điểm có tọa độ (-2;0)?

 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 7:
Đội văn nghệ khối 8 của trường có 3 bạn nam lớp 8A, 3 bạn nữ lớp 8B, 1 bạn nam lớp 8C và 2 bạn nữ lớp 8C. Chọn ngẫu nhiên một bạn trong đội văn nghệ khối 8 để tham gia tiết mục của trường. Số kết quả có thể là
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 8:
Trong hộp bút của bạn Hoa có 5 bút bi xanh, 3 bút bi đỏ và 2 bút bi đen. Xác suất thực nghiệm của biến cố “Bạn Hoa lấy một bút bi đỏ” là
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 10:
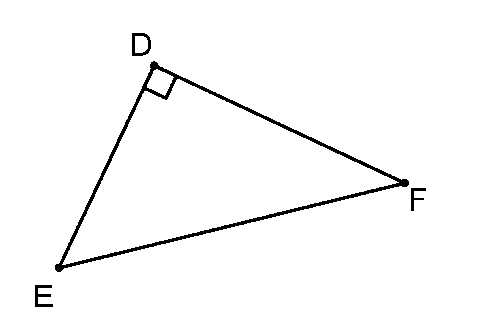
Cho tam giác DEF vuông tại D Biểu thức nào đúng trong các biểu thức sau?
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 11:
Cho ; nếu có , , để theo định nghĩa hai tam giác đồng dạng thì cần bổ sung thêm điều kiện nào?
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 15:
Một xe đạp khởi hành từ điểm A, chạy với vận tốc 15 km/h. Sau đó 6 giờ, một xe hơi đuổi theo với vận tốc 60 km/h. Khi đó, xe hơi chạy trong bao lâu thì đuổi kịp xe đạp?
 Xem đáp án
Xem đáp án
Gọi x (h) là thời gian xe hơi chạy đến lúc đuổi kịp xe đạp ( x > 0)
Quãng đường xe hơi chạy đến lúc đuổi kịp xe đạp là 60x (km)
Thời gian xe đạp chạy đến lúc gặp xe ô tô là x + 6 (h) .
Quãng đường xe đạp chạy đến lúc gặp xe ô tô là 15(x + 6) (km).
Theo đề bài, ta có phương trình
(TMĐK)
Vậy xe hơi chạy trong 2 h thì đuổi kịp xe đạp.
Câu 16:
Một đội thanh niên tình nguyện gồm 11 thành viên đến từ các tỉnh, TP như sau: Kon Tum; Bình Phước; Tây Ninh; Bình Dương; Gia Lai; Bà Rịa – Vũng Tàu; Đồng Nai; Đăk Lăk ; Đăk Nông; Lâm Đồng; TP Hồ Chí Minh, mỗi tỉnh, TP chỉ có đúng một thành viên trong đội. Chọn ngẫu nhiên một thành viên của đội tình nguyện đó.
a) Gọi K là tập hợp gồm các kết quả có thể xảy ra đối với thành viên được chọn. Tính số phần tử của tập hợp K.
b) Tính xác suất của mỗi biến cố sau :
− “Thành viên được chọn ra đến từ vùng Tây Nguyên”.
− “Thành viên được chọn ra đến từ vùng Đông Nam Bộ”.

 Xem đáp án
Xem đáp án
a) Tập hợp K gồm các kết quả xảy ra đối với thành viên được chọn là :
K = {Kon Tum; Bình Phước; Tây Ninh; Bình Dương; Gia Lai; Bà Rịa – Vũng Tàu; Đồng Nai; Đăk Lăk; Đăk Nông; Lâm Đồng; TP Hồ Chí Minh}.
Số phần tử của tập hợp K là 11.
b) Có 5 kết quả thuận lợi cho biến cố “Thành viên được chọn ra đến từ vùng Tây Nguyên” đó là Kon Tum; Gia Lai; Đăk Lăk; Đăk Nông; Lâm Đồng.
Vì thế xác suất của biến cố đó là .
+) Có 6 kết quả thuận lợi cho biến cố “Thành viên được chọn ra đến từ vùng Đông Nam Bộ” đó là Bình Phước; Tây Ninh; Bình Dương; Bà Rịa – Vũng Tàu; Đồng Nai; TP Hồ Chí Minh.
Vì thế xác suất của biến cố đó là .
Câu 17:

 Xem đáp án
Xem đáp án

Ta có SE là trung đoạn nên E là trung điểm của AB .
Xét có E, H lần lượt là trung điểm của AB, BD .
Suy ra EH là đường trung bình của nên .
Áp dụng định lí Pythagore vuông tại H có:
Suy ra
Do đó .
Vậy chiều cao của hộp quà là 12 cm.
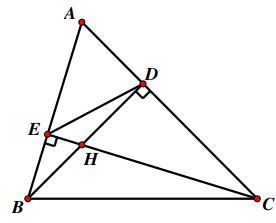
a) Xét và có
;
Do đó .
b) Từ câu a: suy ra .
Do đó
Vậy AE = 2,5 cm
c) Từ câu a: suy ra hay .
Xét và có:
; (cmt)
Do đó
Suy ra (hai góc tương ứng) (1)
Mặt khác, ta có:
• (2)
• (3)
Từ (1), (2) và (3) nên suy ra
Câu 18:
Tìm giá trị nhỏ nhất của phân thức .
 Xem đáp án
Xem đáp án
Ta có .
Vì nên .
Để phân thức B đạt giá trị nhỏ nhất thì biểu thức đạt giá trị lớn nhất.
Khi đó, .
Dấu "=" xảy ra khi và chỉ khi hay .
Vậy giá trị lớn nhất của phân thức B là khi .