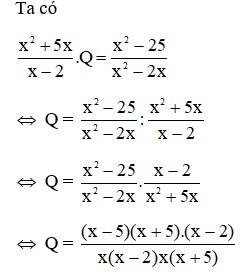13 câu hỏi trắc nghiệm thuộc Trắc nghiệm Phép nhân, phép chia các phân thức đại số có đáp án ( Vận dụng)

Câu 1:

Tìm phân thức Q biết $\frac{x^{2} + 5 x}{x - 2} . Q = \frac{x^{2} - 25}{x^{2} - 2 x}$

A. Q= $\frac{x + 5}{x}$

B.Q= $\frac{x - 5}{x}$

C. Q= $\frac{x + 5}{x^{2}}$

D. Q= $\frac{x - 5}{x^{2}}$

Xem đáp án

Câu 2:

Tìm biểu thức Q, biết $\frac{5 x}{x^{2} + 2 x + 1} . Q = \frac{x}{x^{2} - 1}$

A. $\frac{x + 1}{x - 1}$

B. $\frac{x - 1}{x + 1}$

C. $\frac{x - 1}{5 (x + 1)}$

D. $\frac{x + 1}{5 (x - 1)}$

Xem đáp án

Ta có

Q = $\frac{5 x}{x^{2} + 2 x + 1} . Q = \frac{x}{x^{2} - 1}$

=> Q = $\frac{x}{x^{2} - 1} : \frac{5 x}{x^{2} + 2 x + 1} = \frac{x}{x^{2} - 1} . \frac{x^{2} + 2 x + 1}{5 x}$

= $\frac{x}{(x - 1) (x + 1)} . \frac{{(x + 1)}^{2}}{5 x} = \frac{x + 1}{5 (x - 1)}$

Đáp án cần chọn là: D

Câu 3:

Tìm biểu thức M, biết $\frac{x + 2 y}{x^{3} - 8 y^{3}} . M = \frac{5 x^{2} + 10 x y}{x^{2} + 2 x y + 4 y^{2}}$

A. $5 x (x - 2 y)$

B. 5x(x + 2y)

C. 5x(x – y)

D. x(x – 2y)

Xem đáp án

Câu 4:

Tìm biểu thức M, biết $\frac{x^{2} + x y - 2 y^{2}}{x^{4} - y^{4}} . M = \frac{x + y}{x^{3} + x^{2} y + x y^{2} + y^{3}}$

A. $\frac{x + y}{x - 2 y}$

B. $\frac{x + y}{x + 2 y}$

C. $\frac{x + y}{2 x + y}$

D. $\frac{x - y}{x + 2 y}$

Xem đáp án

Ta có $\frac{x^{2} + x y - 2 y^{2}}{x^{4} - y^{4}} . M = \frac{x + y}{x^{3} + x^{2} y + x y^{2} + y^{3}}$

M = $\frac{x + y}{x^{3} + x^{2} y + x y^{2} + y^{3}} : \frac{x^{2} + x y - 2 y^{2}}{x^{4} - y^{4}}$

M = $\frac{x + y}{x^{3} + x^{2} y + x y^{2} + y^{3}} . \frac{x^{4} - y^{4}}{x^{2} + x y - 2 y^{2}}$

M = $\frac{x + y}{x^{2} (x + y) + y^{2} (x + y)} . \frac{(x^{2} - y^{2}) (x^{2} + y^{2})}{x^{2} + 2 x y - x y - 2 y^{2}}$

M = $\frac{x + y}{(x + y) (x^{2} + y^{2})} . \frac{(x - y) (x + y) (x^{2} + y^{2})}{x^{2} + 2 x y - x y - 2 y^{2}}$

M = $\frac{x + y}{(x + y) (x^{2} + y^{2})} . \frac{(x - y) (x + y) (x^{2} + y^{2})}{x (x + 2 y) - y (x + 2 y)}$

M = $\frac{x + y}{(x + y) (x^{2} + y^{2})} . \frac{(x - y) (x + y) (x^{2} + y^{2})}{(x + 2 y) (x - y)}$

M = $\frac{x + y}{x + 2 y}$

Đáp án cần chọn là: B

Câu 5:

Tìm biểu thức N, biết N: $\frac{x^{2} + x + 1}{2 x + 2} = \frac{x + 1}{x^{3} - 1}$

A. $\frac{1}{2 (x - 1)}$

B. $\frac{1}{x - 1}$

C. $\frac{1}{2 (x + 1)}$

D. $\frac{1}{2 (1 - x)}$

Xem đáp án

Đáp án cần chọn là: A

Câu 6:

Tìm x, biết $\frac{1}{x} . \frac{x}{x + 1} . \frac{x + 1}{x + 2} . \frac{x + 2}{x + 3} . \frac{x + 3}{x + 4} . \frac{x + 4}{x + 5} . \frac{x + 5}{x + 6} = 1$

A. x = -6

B. x = -5

C. x = -7

D. không có x

Xem đáp án

Điều kiện: x $\neq \{0; - 1; - 2; - 3; - 4; - 5; - 6\}$

$\frac{1}{x} . \frac{x}{x + 1} . \frac{x + 1}{x + 2} . \frac{x + 2}{x + 3} . \frac{x + 3}{x + 4} . \frac{x + 4}{x + 5} . \frac{x + 5}{x + 6} = 1$

Câu 7:

Giá trị biểu thức A = $\frac{5^{2} - 1}{3^{2} - 1} : \frac{9^{2} - 1}{7^{2} - 1} : \frac{13^{2} - 1}{11^{2} - 1} : . . . : \frac{55^{2} - 1}{53^{2} - 1}$ là

A. $\frac{9}{28}$

B. $\frac{28}{9}$

C. $\frac{18}{14}$

D. $\frac{3}{28}$

Xem đáp án

A= $\frac{5^{2} - 1}{3^{2} - 1} : \frac{9^{2} - 1}{7^{2} - 1} : \frac{13^{2} - 1}{11^{2} - 1} : . . . : \frac{55^{2} - 1}{53^{2} - 1}$

A= $\frac{5^{2} - 1}{3^{2} - 1} . \frac{7^{2} - 1}{9^{2} - 1} . \frac{11^{2} - 1}{13^{2} - 1} . . . \frac{53^{2} - 1}{55^{2} - 1}$

A= $\frac{4.6}{2.4} . \frac{6.8}{8.10} . \frac{10.12}{12.14} . . . \frac{52.54}{54.56}$

A= $\frac{6}{2} . \frac{6}{10} . \frac{10}{14} . . . . . \frac{52}{56}$

A= $3 . \frac{6}{56} = \frac{9}{28}$

Đáp án cần chọn là: A

Câu 8:

Cho x + y + z ≠ 0 và x = y + z. Chọn đáp án đúng

A. $\frac{{(x y + y z + z x)}^{2} - (x^{2} y^{2} + y^{2} z^{2} + z^{2} x^{2})}{x^{2} + y^{2} + z^{2}} : \frac{{(x + y + z)}^{2}}{x^{2} + y^{2} + z^{2}} = x y$

B. $\frac{{(x y + y z + z x)}^{2} - (x^{2} y^{2} + y^{2} z^{2} + z^{2} x^{2})}{x^{2} + y^{2} + z^{2}} : \frac{{(x + y + z)}^{2}}{x^{2} + y^{2} + z^{2}} = y z$

C. $\frac{{(x y + y z + z x)}^{2} - (x^{2} y^{2} + y^{2} z^{2} + z^{2} x^{2})}{x^{2} + y^{2} + z^{2}} : \frac{{(x + y + z)}^{2}}{x^{2} + y^{2} + z^{2}} = x y z$

D. $\frac{{(x y + y z + z x)}^{2} - (x^{2} y^{2} + y^{2} z^{2} + z^{2} x^{2})}{x^{2} + y^{2} + z^{2}} : \frac{{(x + y + z)}^{2}}{x^{2} + y^{2} + z^{2}} = 1$

Xem đáp án

Ta có $\frac{{(x y + y z + z x)}^{2} - (x^{2} y^{2} + y^{2} z^{2} + z^{2} x^{2})}{x^{2} + y^{2} + x^{2}} : \frac{{(x + y + z)}^{2}}{x^{2} + y^{2} + z^{2}}$

= $\frac{x^{2} y^{2} + y^{2} z^{2} + z^{2} x^{2} + 2 (x y^{2} z + z^{2} y x + y z x^{2}) - (x^{2} y^{2} + y^{2} z^{2} + z^{2} x^{2})}{x^{2} + y^{2} + z^{2}} . \frac{x^{2} + y^{2} + z^{2}}{{(x + y + z)}^{2}}$

= $\frac{2 x y z (x + y + z)}{{(x + y + z)}^{2}} = \frac{2 x y z}{(x + y + z)} = \frac{2 x y z}{2 x} = y z$

(vì x = y + z)

Đáp án cần chọn là: B

Câu 9:

Tính giá trị của biểu thức

T = $[\frac{x^{2} + (a - b) x - a b}{x^{2} - (a - b) x - a b} . \frac{x^{2} - (a + b) x + a b}{x^{2} + (a + b) x + a b}] : [\frac{x^{2} - (b - 1) x - b}{x^{2} + (b + 1) x + b} . \frac{x^{2} - (b + 1) x + b}{x^{2} - (1 - b) x - b}]$

A.1

B. 2

C. 3

D. 4

Xem đáp án

Ta có x² + (a – b)x – ab = x² + ax – bx – ab

= x(x + a) – b(x + a) = (x – b)(x + a)

x² – (a – b)x – ab = x² – ax + bx – ab

= x(x – a) + b(x – a) = (x – a)(x + b)

x² – (a + b)x + ab = x² – ax – bx + ab

= x(x – a) – b(x – a) = (x – b)(x – a)

x² + (a + b)x + ab = x² + ax + bx + ab

= x(x + a) + b(x + a) = (x + a)(x + b)

x² – (b – 1)x – b = x² – bx + x – b

= x(x – b) + x – b = (x – b)(x + 1)

x² + (b + 1)x + b = x² + bx + x + b

= x(x + b) + x + b = (x + b)(x + 1)

x² – (b + 1)x + b = x² – bx – x + b

= x(x – b) – (x – b) = (x – b)(x – 1)

x² – (1 – b)x – b = x² – x + bx – b

= x(x – 1) + b(x – 1) = (x + b)(x – 1)

Khi đó

T= $[\frac{x^{2} + (a - b) x - a b}{x^{2} - (a - b) x - a b} . \frac{x^{2} - (a + b) x + a b}{x^{2} + (a + b) x + a b}] : [\frac{x^{2} - (b - 1) x - b}{x^{2} + (b + 1) x + b} . \frac{x^{2} - (b + 1) x + b}{x^{2} - (1 - b) x - b}]$

= $[\frac{(x - b) (x + a)}{(x - a) (x + b)} . \frac{(x - a) (x - b)}{(x + a) (x + b)}] : [\frac{(x - b) (x + 1)}{(x + b) (x + 1)} . \frac{(x - 1) (x - b)}{(x + b) (x - 1)}]$

= $\frac{{(x - b)}^{2}}{{(x + b)}^{2}} : \frac{{(x - b)}^{2}}{{(x + b)}^{2}} = 1$

Vậy T = 1

Đáp án cần chọn là: A

Câu 10:

Cho M = $\frac{x^{2} + y^{2} + x y}{x^{2} - y^{2}} : \frac{x^{3} - y^{3}}{x^{2} + y^{2} - 2 x y}$ và N = $\frac{x^{2} - y^{2}}{x^{2} + y^{2}} : \frac{x^{2} - 2 x y + y^{2}}{x^{4} - y^{4}}$ . Khi x + y = 6, hãy so sánh M và N

A. M < N

B. M > N

C. M ≥ N

D.M = N

Xem đáp án

Ta có M = $\frac{x^{2} + y^{2} + x y}{x^{2} - y^{2}} : \frac{x^{3} - y^{3}}{x^{2} + y^{2} - 2 x y}$

= $\frac{x^{2} + x y + y^{2}}{x^{2} - y^{2}} . \frac{x^{2} - 2 x y + y^{2}}{x^{3} - y^{3}}$

= $\frac{(x^{2} + x y + y^{2}) {(x - y)}^{2}}{(x - y) (x + y) (x - y) (x^{2} + x y + y^{2})}$

= $\frac{1}{x + y}$ => M = $\frac{1}{x + y}$

Và N = $\frac{x^{2} - y^{2}}{x^{2} + y^{2}} : \frac{x^{2} - 2 x y + y^{2}}{x^{4} - y^{4}}$

= $\frac{x^{2} - y^{2}}{x^{2} + y^{2}} . \frac{x^{4} - y^{4}}{x^{2} - 2 x y + y^{2}}$

= $\frac{(x - y) (x + y) (x^{2} + y^{2}) (x^{2} - y^{2})}{(x^{2} + y^{2}) {(x - y)}^{2}}$

= $\frac{(x + y) (x^{2} - y^{2})}{x - y} = \frac{(x + y) (x - y) (x + y)}{x - y} = (x + y)^{2}$

N = (x + y)²

^{Với x + y = 6 thì M = $\frac{1}{x + y} = \frac{1}{6}$}

Và N = (x + y)² = 6² = 36. Nên M < N

Đáp án cần chọn là: A

Câu 11:

Cho A = $\frac{x^{2} + 1}{3 x} : \frac{x^{2} + 1}{x - 1} : \frac{x^{3} - 1}{x^{2} + x} : \frac{x^{2} + 2 x + 1}{x^{2} + x + 1}$ và B = $\frac{x + 3}{x^{2} - 1} : \frac{x + 4}{x^{2} + 6 x} - \frac{x + 3}{x^{2} - 1} : \frac{x + 4}{x - 4}$ . Khi x = 101, hãy so sánh A và B.

A. B < A

B. B > A

C.B = A

D. B ≤ A

Xem đáp án

Ta có

A= $\frac{x^{2} + 1}{3 x} : \frac{x^{2} + 1}{x - 1} : \frac{x^{3} - 1}{x^{2} + x} : \frac{x^{2} + 2 x + 1}{x^{2} + x + 1}$

= $\frac{x^{2} + 1}{3 x} . \frac{x - 1}{x^{2} + 1} . \frac{x^{2} + x}{x^{3} - 1} . \frac{x^{2} + x + 1}{x^{2} + 2 x + 1}$

= $\frac{x - 1}{3 x} . \frac{x (x + 1)}{(x - 1) (x^{2} + x + 1)} . \frac{x^{2} + x + 1}{x^{2} + 2 x + 1}$

= $\frac{x + 1}{3 (x^{2} + x + 1)} . \frac{x^{2} + x + 1}{{(x + 1)}^{2}} = \frac{1}{3 (x + 1)}$

Và

B = $\frac{x + 3}{x^{2} - 1} : \frac{x + 4}{x^{2} + 6 x} - \frac{x + 3}{x^{2} - 1} : \frac{x + 4}{x - 4}$

= $\frac{x + 3}{x^{2} - 1} . \frac{x^{2} + 6 x}{x + 4} - \frac{x + 3}{x^{2} - 1} . \frac{x - 4}{x + 4}$

= $\frac{x + 3}{x^{2} - 1} . (\frac{x^{2} + 6 x}{x + 4} - \frac{x - 4}{x + 4})$

= $\frac{x + 3}{(x - 1) (x + 1)} . \frac{x^{2} + 6 x - x + 4}{x + 4}$

= $\frac{x + 3}{(x - 1) (x + 1)} . \frac{x^{2} + 5 x + 4}{x + 4}$

= $\frac{x + 3}{(x - 1) (x + 1)} . \frac{(x + 1) (x + 4)}{x + 4} = \frac{x + 3}{x - 1}$

Thay x = 101 vào A = $\frac{1}{3 (x + 1)}$ ta được

A= $\frac{1}{3 (101 + 1)} = \frac{1}{3.102} = \frac{1}{306}$

Thay x = 101 vào B = $\frac{x + 3}{x - 1}$ ta được

B= $\frac{101 + 3}{101 - 1} = \frac{104}{100}$

Nhận thấy B = $\frac{104}{100}$ > 1; A = $\frac{1}{306}$ < 1 => B > A

Đáp án cần chọn là: B

Câu 12:

Rút gọn và tính giá trị biểu thức A = $\frac{x - 6}{x^{2} + 1} . \frac{3 x^{2} - 3 x + 3}{x^{2} - 36} + \frac{x - 6}{x^{2} + 1} . \frac{3 x}{x^{2} - 36}$ khi x = 994.

Xem đáp án

Ta có A= $\frac{x - 6}{x^{2} + 1} . \frac{3 x^{2} - 3 x + 3}{x^{2} - 36} + \frac{x - 6}{x^{2} + 1} . \frac{3 x}{x^{2} - 36}$

= $\frac{x - 6}{x^{2} + 1} (\frac{3 x^{2} - 3 x + 3}{x^{2} - 36} + \frac{3 x}{x^{2} - 36})$

= $\frac{x - 6}{x^{2} + 1} . \frac{3 x^{2} - 3 x + 3 + 3 x}{x^{2} - 36}$

= $\frac{x - 6}{x^{2} + 1} . \frac{3 x^{2} + 3}{(x - 6) (x + 6)}$

= $\frac{x - 6}{x^{2} + 1} . \frac{3 (x^{2} + 1)}{(x - 6) (x + 6)} = \frac{3}{x + 6}$

Thay x = 994 vào A = $\frac{3}{x + 6}$ ta được A = $\frac{3}{994 + 6} = \frac{3}{1000}$

Đáp án cần chọn là: B

Câu 13:

Tính giá trị biểu thức C = $\frac{2 x^{3} y^{2}}{x^{2} y^{5} z^{2}} : \frac{5 x^{2} y}{4 x^{2} y^{5}} : \frac{- 8 x^{3} y^{2} z^{3}}{15 x^{5} y^{2}}$ khi x = 4; y =1; z = -2.

A. C = 6

B. C = -6

C.C = -3

D. C = 3

Xem đáp án

Ta có C = $\frac{2 x^{3} y^{2}}{x^{2} y^{5} z^{2}} : \frac{5 x^{2} y}{4 x^{2} y^{5}} : \frac{- 8 x^{3} y^{2} z^{3}}{15 x^{5} y^{2}}$

= $\frac{2 x^{3} y^{2}}{x^{2} y^{5} z^{2}} . \frac{4 x^{2} y^{5}}{5 x^{2} y} : \frac{- 8 x^{3} y^{2} z^{3}}{15 x^{5} y^{2}} = \frac{8 x^{5} y^{7}}{5 x^{4} y^{6} z^{2}} : \frac{- 8 x^{3} y^{2} z^{3}}{15 x^{5} y^{2}}$

= $\frac{8 x y}{5 z^{2}} : \frac{- 8 x^{3} y^{2} z^{3}}{15 x^{5} y^{2}} = \frac{8 x y}{5 z^{2}} . \frac{15 x^{5} y^{2}}{- 8 x^{3} y^{2} z^{3}}$

= $\frac{120 x^{6} y^{3}}{- 40 x^{3} y^{2} z^{5}} = \frac{- 3 x^{3} y}{z^{5}}$

Vậy C = $\frac{- 3 x^{3} y}{z^{5}}$

Thay x = 4; y =1; z = -2 vào C = $\frac{- 3 x^{3} y}{z^{5}}$ ta được C = $\frac{- {3.4}^{3} . 1}{{(- 2)}^{5}}$ = 6

Đáp án cần chọn là: A