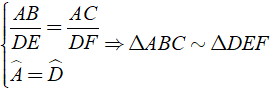8 câu hỏi trắc nghiệm thuộc Trắc nghiệm chuyên đề Toán 8 Chủ đề 5: Các trường hợp đồng dạng của tam giác có đáp án

Trắc nghiệm chuyên đề Toán 8 Chủ đề 5: Các trường hợp đồng dạng của tam giác có đáp án

Đề số 1

Trắc nghiệm chuyên đề Toán 8 Chủ đề 5: Các trường hợp đồng dạng của tam giác có đáp án

1186 lượt thi
8 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho Δ ABC vuông góc tại A có BC = 5cm, AC = 3cm, EF = 3cm, DE = DF = 2,5cm. Chọn phát biểu đúng?

A. Δ ABC ∼ Δ DEF

B. ABCˆ = EFDˆ

C. ACBˆ = ADFˆ

D. ACBˆ = DEFˆ

Xem đáp án

Hướng dẫn giải:

Áp dụng định lý Py – ta – go vào tam giác ABC vuông tại A ta được

BC² = AC² + AB² ⇒ AB = √ (BC² - AC²) = √ (5² - 3²) = 4( cm )

Ta có: cos ACBˆ = AC/BC = 3/5

Xét tam giác DEF có:

$\cos \hat{D E F} = \frac{D E^{2} + E F^{2} - D F^{2}}{2 D E . E F} = \frac{3^{2} + 2, 5^{2} - 3^{2}}{2.3.2, 5} = \frac{3}{5}$

Khi đó ACBˆ = DEFˆ

Chọn đáp án B.

Câu 2:

Cho hai tam giác Δ RSK và Δ PQM có: RS/PQ = RK/PM = SK/QM thì:

A. Δ RSK ∼ Δ PQM

B. Δ RSK ∼ Δ MPQ

C. Δ RSK ∼ Δ QPM

D. Δ RSK ∼ Δ QMP

Xem đáp án

Hướng dẫn giải:

Ta có: RS/PQ = RK/PM = SK/QM ⇒ Δ RSK ∼ Δ PQM

Chọn đáp án A.

Câu 3:

Nếu Δ RSK ∼ Δ PQM có: RS/PQ = RK/PM = SK/QM thì

A. RSKˆ = PQMˆ

B. RSKˆ = PMQˆ

C. RSKˆ = MPQˆ

D. RSKˆ = QPMˆ

Xem đáp án

Hướng dẫn giải:

Ta có Δ RSK ∼ Δ PQM ⇔

$\{\begin{cases} \hat{R S K} = \hat{P Q M} \\ \hat{R K S} = \hat{P M Q} \\ \hat{K R S} = \hat{M P Q} \end{cases}$

Chọn đáp án A.

Câu 4:

Chọn câu trả lời đúng?

A. Δ ABC, Δ DEF;AB/DE = AC/DF;Bˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF

B. Δ ABC, Δ DEF;AB/DE = AC/DF;Cˆ = Fˆ ⇒ Δ ABC ∼ Δ DEF

C. Δ ABC, Δ DEF;AB/DE = AC/DF;Aˆ = Dˆ ⇒ Δ ABC ∼ Δ DEF

D. Δ ABC, Δ DEF;AB/DE = AC/DF;Aˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF

Xem đáp án

Hướng dẫn giải:

Ta có:

Chọn đáp án C.

Câu 5:

Cho hình bên, ABCD là hình thang ( AB//CD ) có AB = 12,5cm; CD = 28,5cm; DABˆ = DBCˆ. Tính độ dài đoạn BD gần nhất bằng bao nhiêu?

Cho hình bên, ABCD là hình thang ( AB//CD ) có AB = 12,5cm; CD = 28,5cm; DABˆ = DBCˆ (ảnh 1)

A. 17,5

B. 18

C. 18,5

D. 19

Xem đáp án

Hướng dẫn giải:

Xét Δ ABD và Δ BDC có:

$\{\begin{array}{l} \hat{B A D} = \hat{D B C} \\ \hat{A B D} = \hat{B D C} \end{array} \Rightarrow ∆ A B D ~ ∆ B D C (g - g)$

⇒ AB/BD = AD/BC = BD/DC

hay 12,5/x = x/28,5 ⇒ x² = 1425/4 ⇔ x ≈ 18,87

Chọn đáp án D.

Câu 6:

Tứ giác ABCD có AB = 2cm; BC = 6cm; CD = 8cm; DA = 3cm và BD = 4cm. Chứng minh rằng:

a) Δ BAD ∼ Δ DBC

b) ABCD là hình thang

Tứ giác ABCD có AB = 2cm; BC = 6cm; CD = 8cm; DA = 3cm và BD = 4cm. (ảnh 1)

Xem đáp án

Hướng dẫn giải:

a) Ta có:

BA/BD = AD/BC = BD/CD = 1/2 ⇒ Δ BAD ∼ Δ DBC ( c - c - c )

b) Ta có: Δ BAD ∼ Δ DBC

⇒ ABDˆ = BDCˆ nên AB//CD

⇒ ABCD là hình thang.

Câu 7:

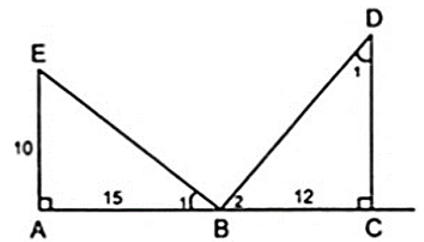
Cho hình vẽ như bên, biết EBAˆ = BDCˆ

a) Trong hình vẽ có bao nhiêu tam giác vuông? Kể tên các tam giác vuông đó.

b) Cho AE = 10cm, AB = 15cm, BC = 12cm. Hãy tính độ dài các đoạn thẳng CD, BE, BD và ED (làm tròn đến chữ số thập phân thứ nhất)

c) So sánh diện tích tam giác BDE với tổng diện tích hai tam giác AEB và BCD

Cho hình vẽ như bên, biết EBAˆ = BDCˆ a) Trong hình vẽ có bao nhiêu tam giác vuông (ảnh 1)

Xem đáp án

Hướng dẫn giải:

a) Từ giả thiết và tính chất về góc của tam giác vuông BCD ta có:

\{\begin{cases} \hat{B_{1}} = \hat{D_{1}} \\ \hat{B_{2}} + \hat{D_{1}} = 90^{0} \end{cases}

⇒ Bˆ₁ + Bˆ₂ = 90⁰ ⇒ EBDˆ = 90⁰ , do ABCˆ là góc bẹt

Vậy trong hình vẽ có 3 tam giác vuông là ABE, BCD, EDB

b) Ta có:

$\{\begin{cases} \hat{A} = \hat{C} \\ \hat{B_{1}} = \hat{D_{1}} \end{cases}$

⇒ Δ CDB ∼ Δ ABE ( g - g )

⇒ CD/AB = BC/AE

hay CD/15 = 10/12 ⇔ CD = (10.15)/12 ⇒ CD = 18 ( cm )

Áp dụng định lý Py – ta – go vào tam giác vuông ABE có:

BE² = AE² + AB² ⇒ BE² = 10² + 15² ⇒ BE ≈ 18,0( cm )

Áp dụng định lý Py – ta – go vào tam giác vuông BCD có:

BD² = CD² + BC² ⇒ BD² = 18² + 12² = 468 ⇒ BD ≈ 21,6( cm )

Áp dụng định lý Py – ta – go vào tam giác vuông EBD có:

ED² = BD² + BE² ⇒ ED² = 325 + 468 = 793 ⇒ ED ≈ 28,2( cm )

c) Ta có:

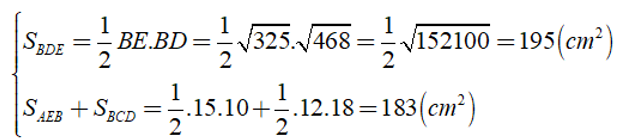
Cho hình vẽ như bên, biết EBAˆ = BDCˆ a) Trong hình vẽ có bao nhiêu tam giác vuông (ảnh 2)

Vậy S_BED > S_AEB + S_BCD

Câu 8:

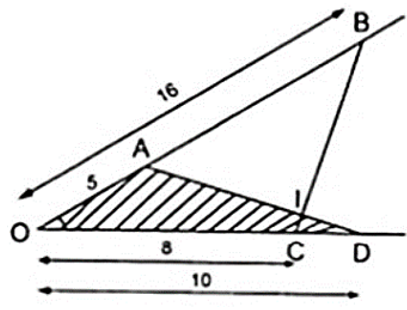
Trên một cạnh của một góc xOy ( Ox ≠ Oy ) đặt các đoạn thẳng OA = 5cm, OB = 16cm Trên cạnh thứ hai của góc đó đặt các đoạn thẳng OC = 8cm, OD = 10cm.

a) Chứng minh Δ OCB ∼ Δ OAD

b) Gọi I là giao điểm của các cạnh AD và BC. Chứng minh rằng Δ IAB và Δ ICD có các góc bằng nhau từng đôi một

Trên một cạnh của một góc xOy ( Ox ≠ Oy ) đặt các đoạn thẳng OA = 5cm, OB = 16cm (ảnh 1)

Xem đáp án

Hướng dẫn giải:

a) Xét Δ OCB và Δ OAD có

$\{\begin{cases} \hat{O} = \hat{O} \\ \frac{O A}{O D} = \frac{O C}{O B} = \frac{1}{2} \Rightarrow \frac{O A}{O C} = \frac{O D}{O B} \end{cases}$

⇒ Δ OCB ∼ Δ OAD ( c - g - c )

b) Ta có: Δ OCB ∼ Δ OAD

⇒ ADOˆ = CBOˆ hay IDCˆ = IBAˆ

Mà CIDˆ = AIBˆ (vì đối đỉnh) ⇒ ICDˆ = IAB

Bắt đầu thi ngay