6 câu hỏi trắc nghiệm thuộc Dạng 2. Sử dụng định nghĩa, tính chất của hình vuông để chứng minh các quan hệ bằng nhau, song song, vuông góc, thẳng hàng có đáp án

Bài tập Toán 8 Chủ đề 15: Hình vuông có đáp án

Dạng 2. Sử dụng định nghĩa, tính chất của hình vuông để chứng minh các quan hệ bằng nhau, song song, vuông góc, thẳng hàng có đáp án

981 lượt thi
6 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, trên cạnh CD lấy điểm N sao cho BM = CN và $A M ⊥ B N$ .

Xem đáp án

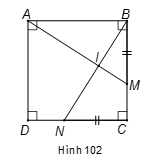
Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, trên cạnh CD lấy điểm N sao cho BM = CN và AM vuông BN (ảnh 1)

Áp dụng định nghĩa và giả thiết vào hình vuông ABCD, ta được:

$\{\begin{matrix} A B = B C \\ \hat{A} = \hat{B} = 90^{0} \\ B M = C N \end{matrix}$

$\Rightarrow Δ A B M = Δ B C N$ (c.g.c), nên AM = BN.

Gọi I là giao diểm của AM và BN.

Áp dụng tính chất về góc vào tam giác vuông ABM và BCN kết quả của hai tam giác bằng nhau, ta được:

$\{\begin{matrix} \hat{A_{1}} + \hat{M_{1}} = 90^{0} \\ \hat{B_{1}} = \hat{A_{1}} \end{matrix} \Rightarrow \hat{B_{1}} + \hat{M_{1}} = 90^{0}$ (1)

Áp dụng tính chất về góc vào tam giác BIM ta có $\hat{B_{1}} + \hat{M_{1}} + \hat{I_{1}} = 180^{0}$ (2)

Từ (1) và (2) suy ra $\hat{I} = 180^{0} - 90^{0} = 90^{0}$ hay $A M ⊥ B N$ .

Câu 2:

M P ⊥ N Q \Rightarrow M P = N Q

Xem đáp án

b) $M P ⊥ N Q \Rightarrow M P = N Q$ .

Xét hai tam giác MEI và NEI có $\hat{I_{1}} = \hat{I_{2}}$ vì đối đỉnh, $\hat{O} = \hat{E} = 90^{0}$ suy ra $\hat{M_{1}} = \hat{N_{1}}$ (1) vì hai tam giác, có hai cặp góc bằng nhau thì cặp góc còn lại cũng bằng nhau.

Lại có $\hat{H} = \hat{K} = 90^{0}, M H = N K$ (2) theo câu a).

Từ (1) và (2) suy ra $Δ M H B = Δ N K Q$ (c-g-c) nên MP = NQ.

Câu 3:

Cho hình vuông ABCD cạnh a. Trên hai cạnh BC, BD lấy hai điểm M, N sao cho $\hat{M A N} = 45^{0}$ , trên tia đối của tia DC lấy điểm K sao cho DK = BM. Hãy tính:

a) Số đo góc KAN.

Xem đáp án

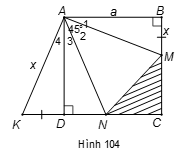
Cho hình vuông ABCD cạnh a. Trên hai cạnh BC, BD lấy hai điểm M, N sao cho MAN = 45 độ. Hãy tính: a) Số đo góc KAN. (ảnh 1)

a) Áp dụng định nghĩa và giả thiết vào hình vuông ABCD, ta được $\{\begin{matrix} \hat{A} = \hat{D} = 90^{0} \\ A B = A D, B M = D K \end{matrix}$

$\Rightarrow Δ A B M = Δ A D K$ (c-g-c).

Áp dụng kết quả của hai tam giác bằng nhau ở trên và giả thiết, ta có:

$\{\begin{matrix} \hat{A_{1}} + \hat{A_{2}} + \hat{A_{3}} = 90^{0} \\ \hat{A_{1}} = \hat{A_{4}}, \hat{A_{2}} = 45^{0} \end{matrix} \Rightarrow \hat{K A N} = \hat{A_{3}} + \hat{A_{4}} = \hat{A_{1}} + \hat{A_{3}} = 90^{0} - 45^{0} = 45^{0}$ .

Câu 4:

b) Chu vi tam giác MCN theo a .

Xem đáp án

b) Đặt BM = DK = x thì $K N = x + D N, M C = a - x, C N = a - D N$ .

Từ kết quả của hai tam giác bằng nhau ở câu a) và giả thiết, ta được:

$\{\begin{matrix} A M = A K, A N = A N \\ \hat{M A N} = \hat{K A N} = 45^{0} \end{matrix} \Rightarrow Δ A M N = Δ A K N$ (c-g-c) suy ra MN = KN.

Vậy chu vi tam giác MCN bằng $M C + C N + N M = a - x + a - D N + x + D N = 2 a$ .

Câu 5:

Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, qua A kẻ $A N ⊥ A M$ (điểm N thuộc tia đối của tia DC). Gọi I là trung điểm của MN. Chứng minh rằng:

a) AM = AN.

Xem đáp án

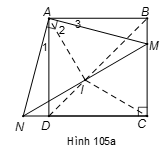
Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, qua A kẻ AN vuông AM Chứng minh rằng: a) AM = AN. (ảnh 1)

a) Áp dụng định nghĩa và giả thiết vào hình vuông ABCD, ta được:

$\{\begin{matrix} \hat{A} = \hat{B} = \hat{D} \\ \hat{A_{1}} + \hat{A_{2}} = \hat{A_{2}} + \hat{A_{3}} = \hat{A} = 90^{0} \\ A B = A D \end{matrix} \Rightarrow \{\begin{matrix} \hat{B} = \hat{D} = 90^{0} \\ A B = A D \\ \hat{A_{3}} = \hat{A_{1}} \end{matrix} \Rightarrow Δ A B M = Δ A D N$ (c-g-c).

Do đó AM = AN.

Câu 6:

b) Ba điểm B, I, D thẳng hàng.

Xem đáp án

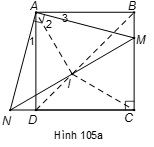
Cách 1 (hình 105a): Nối IA, IC thì IA và IC lần lượt là các đường trung tuyến ứng với cạnh huyền của hai tam giác vuông AMN, CMN.

Áp dụng tính chất đường trung tuyến ứng với cạnh huyền vào hai tam giác vuông trên và định nghĩa hình vuông ta được $\{\begin{matrix} I A = I C = \frac{1}{2} M N \\ B A = B C \end{matrix}$ .

Điều này chứng tỏ hai điểm B và I cách đều hai điểm A và C nên BI là đường trung trực của đoạn AC. Mặt khác theo tính chất về đường chéo của hình vuông thì BD là trung trực của AC mà đoạn AC thì chỉ có một đường trung trực nên BI trùng với BD hay B, I, D thẳng hàng.

Cách 2 (hình 105b):

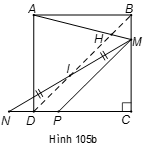
Qua M kẻ MP // BD (1) (điểm $P \in D C$ ) suy ra DI // MP (2).

Lại có NI = MI (3) theo giả thiết. Từ (2) và (3) suy ra ND = DP (4)
theo định lí đường trung bình.

Từ (3) và (4) ta có DI là đường trung bình của tam giác NMP.

Áp dụng định lí đường trung bình vào tam giác NMP ta được DI // MP (5).
Từ (1) và (5) suy ra B, I, D thẳng hàng, vì từ điểm I ở ngoài đường thẳng MP chỉ kẻ được một đường thẳng song song với MP.

Cách 3: Qua M kẻ MH // ND (1) (điểm $H \in B D$ ) thì $\hat{D_{1}} = \hat{H_{1}}$ (2) do đồng vị.

Mà BD là đường chéo của hình vuông ABCD nên BD là đường phân giác của hai góc vuông B và D do đó $\hat{D_{1}} = \hat{H_{1}} = 45^{0}$ (3).

Từ (2) và (3) ta có BM = MH (4) vì trong một tam giác, đối diện với hai góc bằng nhau là hai cạnh bằng nhau.

Kết hợp (1) với (4) ta được tứ giác NHMD có hai cạnh đối song song và bằng nhau nên nó là hình bình hành.

Áp dụng tính chất về đường chéo vào hình bình hành NHMD, ta được đường chéo DH đi qua trung điểm I của đường chéo NM nên BD đi qua I.

Điều đó chứng tỏ B, I, D thẳng hàng.

Bắt đầu thi ngay