Đề thi Học kì 1 Toán lớp 8 cực hay, có đáp án (Đề 2)
-
3870 lượt thi
-
12 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 7:
Cho hình chữ nhật ABCD có AB = 6 cm, BC = 8cm. M, N, P, Q là trung điểm các cạnh của hình chữ nhật. Tổng diện tích các tam giác có trong hình là:
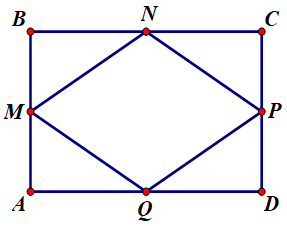
Xem đáp án
Chọn D
Câu 8:
Trong hình dưới, biết ABCD là hình thang vuông, tam giác BMC đều. Số đo của góc ABC là:
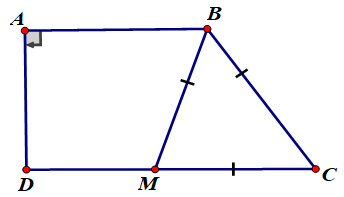
Xem đáp án
Chọn D
Câu 9:
Phần tự luận (8 điểm)
Phân tích thành nhân tử
Xem đáp án
a) x6 – x4 + 2x3 + 2x2
= x2(x4 – x2 + 2x + 2)
= x2[x2(x2 – 1) + 2(x + 1)]
= x2. [x2.(x -1).(x + 1) + 2(x+ 1)]
= x2 (x+ 1).[x2(x- 1)+ 2]
= x2(x + 1)(x3 – x2 + 2)
= x2(x + 1)[(x3 + 1) – (x2 – 1)]
= x2(x + 1).[(x + 1).(x2 – x + 1) - (x - 1).(x + 1)]
= x2(x + 1)(x + 1)( x2 – x + 1 – x + 1)
= x2(x + 1)2(x2 – 2x + 2).
b) 4x4 + y4 = 4x4 + 4x2y2 + y4 - 4x2y2
= (2x2 + y2)2 - (2xy)2
= (2x2 + y2 + 2xy)(2x2 + y2 - 2xy)
Câu 10:
Cho biểu thức :
a) Rút gọn biểu thức P
b) Tính giá trị biểu thức P với x = 1/2
Xem đáp án
a) Ta có: 2x2 + 8 = 2(x2 + 4).
8 – 4x + 2x2 – x3
= (8 – x3) - ( 4x - 2x2)
= (2 – x).(4 + 2x + x2) - 2x.(2 - x)
= (2 – x).(4 + 2x + x2 – 2x)
= (2 - x). (4 + x2 )
* Do đó:
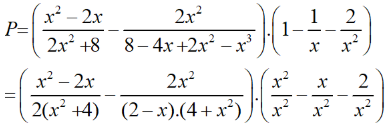
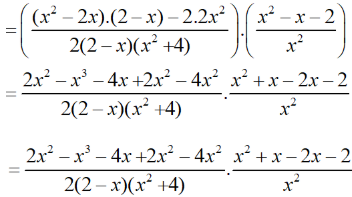
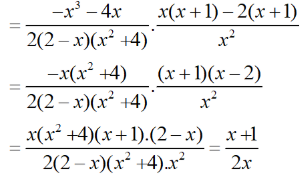
b) Tại hàm số đã cho xác định nên thay vào biểu thức rút gọn của P ta được:
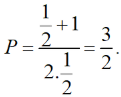
Câu 11:
Chứng tỏ rằng đa thức : luôn luôn lớn hơn 0 với mọi x
Xem đáp án
P = x2 - 2x + 2 = (x – 1)2 + 1
Do (x – 1)2 ≥ 0 ∀x nên (x – 1)2 + 1 ≥ 1 ∀x
Vậy P luôn lớn hơn 0 với mọi x.
Câu 12:
Cho ΔABC cân tại A có AB = 5cm; BC = 6cm. Kẻ phân giác trong AM (M ∈ BC) . Gọi O là trung điểm của AC và K là điểm đối xứng của M qua O.
a) Tính diện tích tam giác ABC.
b) Tứ giác ABMO là hình gì? Vì sao?
c) Để tứ giác AMCK là hình vuông thì tam giác ABC phải có thêm điều kiện gì?
Xem đáp án
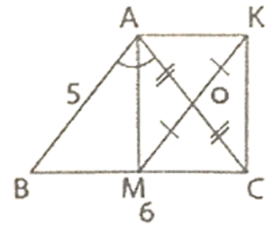
a) Vì M là trung điểm của BC nên:
BM = BC/2 = 6/2 = 3(cm)
Tam giác ABC cân tại A, lại có AM là đường phân giác nên AM cũng là đường cao. Do đó tam giác AMB vuông tại M.
Suy ra: AM2 = AB2 - BM2 (Định lí Pytago)
= 52 - 32 = 16(cm)
Suy ra AM = 4cm
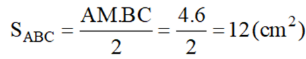
b) ΔAMC vuông tại M có MO là đường trung tuyến nên OM = OA.
Suy ra ∠OAM = ∠OMA ( ΔAMO cân tại O)
Lại có ∠OAM = ∠MAB (AM là tia phân giác góc BAC)
Suy ra ∠OMA = ∠MAB
Mà đây là 2 góc ở vị trí so le trong
Suy ra OM // AB
Vậy tứ giác ABMO là hình thang.
c) Tứ giác AMCK có OA = OC; OM = OK nên tứ giác AMCK là hình bình hành . Lại có ∠AMC = 90o (chứng minh trên) nên tứ giác AMCK là hình chữ nhật.
Hình chữ nhật AMCK là hình vuông
⇔ AM = MC = BM
⇔ AM = BC/2
⇔ ΔABC vuông cân tại A.