Cho có AB < AC, AH là đường cao. Gọi M, N, K lần lượt là trung điểm của AB, AC, BC.
a) Chứng minh MNKH là hình thang cân.
 Giải bởi Vietjack
Giải bởi Vietjack
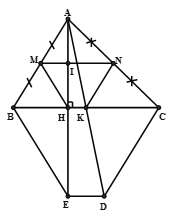
a) MN là đường trung bình của hay
và
cân tại A nên (1)
NK là đường trung bình của (hai góc ở vị tri so le trong) (2)
Từ (1) và (2) suy ra (so le trong) hay
Tứ giác MNHK có MN // HK nên tứ giác là hình thang, lại có là hình thang cân.
Cho tam giác ABC vuông tại A, đường cao AH. Gọi M là trung điểm của HC, K là trung điểm của AH. Chứng minh rằng BK vuông góc với AM.
Cho tam giác ABC. Trên tia đối của tia BC lấy điểm D sao cho BD = AB. Trên tia đối của tia CD lấy điểm E sao cho CE = AC. Gọi H là chân đường vuông góc kẻ từ D đến AD, K là chân đường vuông góc kẻ từ C đến AE.
a) Chứng minh rằng HK song song với DE.
Cho tứ giác ABCD có AB = CD. Gọi E, F lần lượt là trung điểm của AC, DB. Đường thẳng EF lần lượt cắt AB, CD tại H,K. Chứng minh rằng:
Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm của AH, E là giao điểm của BI và AC. Tính các độ dài AE và EC, biết AH = 12 cm, BC = 18 cm.
c) Nếu Khi đó trên cạnh AB lấy điểm E sao cho AB = 3AE Chứng minh BD, CE, AM đồng quy.
Cho có trung tuyến AM, I là một điểm thuộc đoạn thẳng AM, BI cắt AC ở D.
a) Nếu Khi đó hãy chứng minh I là trung điểm của AM.
Hình thang cân ABCD (ABB // CD) có AB = 4 cm, CD = 10 cm, BD = 5 cm. Tính khoảng cách từ trung điểm I của BD đến cạnh CD.
b) Trên tia AH và AK lần lượt lấy điểm E và D sao cho H là trung điểm của AE và K là trung điểm của AD. Chứng minh tứ giác BCDE là hình thang cân.